视觉里程计（1）----libviso

视觉里程计（1）

---

数据集链接：Karlsruhe Dataset: Stereo Video Sequences + rough GPS Poses

github代码 ：
https://github.com/srv/viso2
https://github.com/BrainSpawnInfosphere/libviso2

---

libviso2【转载】

　libviso一直以来被称为在视觉里程计(VO)中的老牌开源算法。它通过corner,chessboard两种kernel的响应以及非极大值抑制的方式提取特征，并用sobel算子与原图卷积的结果作为特征点的描述子。在位姿的计算方面，则通过 RANSAC R A N S A C 迭代的方式，每次迭代随机抽取3个点，根据这三个点，用高斯牛顿法计算出一个 RT R T 矩阵，表示两帧图像之间，相机的姿态变换。而位姿的计算也是libviso 中较为抽象的一部分，接下来，本文将在读者已经对立体视觉的基本原理，以及libviso的场景流匹配熟悉的前提下，对这个过程进行详细分析。

1 运动描述

在libviso的实际位姿计算过程中，实质上是通过含有6个变量的向量

T={rx,ry,rz,tx,ty,tz} T = { r x , r y , r z , t x , t y , t z }

来表示位姿变换的：
其中 rx,ry,rz r x , r y , r z 和 tx,ty,tz t x , t y , t z 分别表示两帧之间相机绕 x,y,z x , y , z 轴之间的旋转和平移。计算出这6个变量之后，再转换成描述两帧之间位置变化的 R|t R | t 矩阵。

2 位姿计算过程

在位姿计算的过程中，输入的是n组通过场景流匹配得到的二维坐标点，每组4个：
(u1c,v1c),(u1p,v1p),(u2c,v2c),(u1p,v1p) ( u 1 c , v 1 c ) , ( u 1 p , v 1 p ) , ( u 2 c , v 2 c ) , ( u 1 p , v 1 p ) ，
分别代表左图、右图，当前时刻，上一时刻图像中的匹配点（这里用了与代码中相同的符号表示，1下标代表左图，2代表右图，c代表上一阵，p代表当前帧）,
(X1c,Y1c,Z1c),(X1p,Y1p,Z1p),(X2c,Y2c,Z2c),(X1p,Y1p,Z1p) ( X 1 c , Y 1 c , Z 1 c ) , ( X 1 p , Y 1 p , Z 1 p ) , ( X 2 c , Y 2 c , Z 2 c ) , ( X 1 p , Y 1 p , Z 1 p )
是其对应的三维坐标，根据立体视觉的原理，三维坐标可以通过匹配点坐标结合相机内参数算出。输出是1中描述的6个变量。这6个变量是通过RANSAC迭代，在每次迭代中都从匹配点中随机抽取3个点，基于这3个点，通过高斯牛顿法的方式求出来的。计算出一次迭代中的参数之后，利用这个参数计算出局内点(inlier)的占比。最终取占比最高的参数，得到结果。下面将对每次迭代中进行的操作细节进行分析。

2.1 参数的更新

在每次迭代中，参数是通过梯度下降的方式求出来的。而高斯牛顿实质上也是一种通过迭代求解的方式。位姿解算的过程，可以看成是在 RANSAC R A N S A C 迭代中，再嵌套了一个迭代求解过程。高斯牛顿法计算的过程中，主要的计算工作包括两步：残差以及雅克比的计算，参数的迭代。
2.1.1 残差以及雅克比的计算

假设在当前的梯度下降迭代(第i次)中，参数的值为
Ti=rxi,ryi,rzi,txi,tyi,tzi T i = r x i , r y i , r z i , t x i , t y i , t z i
，当前的迭代，是根据 RANSAC R A N S A C 中抽取的3个点，更新这6个参数的值，使之更加接近正确解。

对于 rxi,ryi,rzi r x i , r y i , r z i 首先，计算这三个量对应的旋转矩阵 R R ，如下所示(为了简便，以下 x x 指代rx,y与z r x , y 与 z 以此类推)

Rx=⎡⎣⎢1000cos(x)sin(x)0−sin(x)cos(x)⎤⎦⎥ R x = [ 1 0 0 0 c o s ( x ) − s i n ( x ) 0 s i n ( x ) c o s ( x ) ]

Ry=⎡⎣⎢cos(y)0−sin(y)010sin(y)0cos(y)⎤⎦⎥ R y = [ c o s ( y ) 0 s i n ( y ) 0 1 0 − s i n ( y ) 0 c o s ( y ) ]

Rz=⎡⎣⎢cos(z)sin(z)0−sin(z)cos(z)0001⎤⎦⎥ R z = [ c o s ( z ) − s i n ( z ) 0 s i n ( z ) c o s ( z ) 0 0 0 1 ]

R=Rx∗Ry∗Rz=[cos(y)cos(z)cos(x)sin(z)+cos(z)sin(x)sin(y)sin(x)sin(z)−cos(x)cos(z)sin(y)−cos(y)sin(z)cos(x)cos(z)−sin(x)sin(y)sin(z)cos(z)sin(x)+cos(x)∗sin(y)∗sin(z)sin(y)−cos(y)sin(x)cos(x)cos(y)] R = R x ∗ R y ∗ R z = [ c o s ( y ) c o s ( z ) − c o s ( y ) s i n ( z ) s i n ( y ) c o s ( x ) s i n ( z ) + c o s ( z ) s i n ( x ) s i n ( y ) c o s ( x ) c o s ( z ) − s i n ( x ) s i n ( y ) s i n ( z ) − c o s ( y ) s i n ( x ) s i n ( x ) s i n ( z ) − c o s ( x ) c o s ( z ) s i n ( y ) c o s ( z ) s i n ( x ) + c o s ( x ) ∗ s i n ( y ) ∗ s i n ( z ) c o s ( x ) c o s ( y ) ]

然后分别计算 R R 中关于x,y,z x , y , z 的偏导数，如下所示:

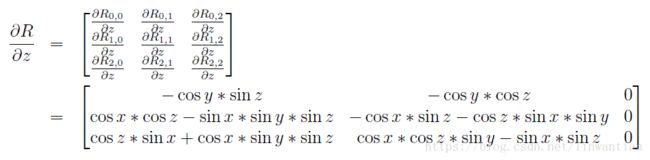
假设 X1p,Y1p,Z1p X 1 p , Y 1 p , Z 1 p 为左图匹配点对应的三维坐标，根据当前的参数 R,tx,ty,tz R , t x , t y , t z ，可以计算出在目前参数下， (X1c,Y1c,Z1c) ( X 1 c , Y 1 c , Z 1 c ) 的估计值：

⎡⎣⎢X1cY1cZ1c⎤⎦⎥=R∗⎡⎣⎢X1pY1pZ1p⎤⎦⎥+⎡⎣⎢txtytz⎤⎦⎥ [ X 1 c Y 1 c Z 1 c ] = R ∗ [ X 1 p Y 1 p Z 1 p ] + [ t x t y t z ]

根据对极几何原理, (X2c,Y2c,Z2c) ( X 2 c , Y 2 c , Z 2 c ) ，可以通过以下方式求得

⎡⎣⎢X2cY2cZ2c⎤⎦⎥=⎡⎣⎢X1c−bY1cZ1c⎤⎦⎥ [ X 2 c Y 2 c Z 2 c ] = [ X 1 c − b Y 1 c Z 1 c ]

其中b为立体相机基线长度。将 (X1c,Y1c,Z1c),(X2c,Y2c,Z2c) ( X 1 c , Y 1 c , Z 1 c ) , ( X 2 c , Y 2 c , Z 2 c ) 变换回对应的二维坐标的过程，称为重投影，具体计算方式如下：

u=fXZ u = f X Z

v=fYZ v = f Y Z

给定一个重投影后的二维坐标点 (u,v) ( u , v ) ，其关于 Ti T i 的雅克比矩阵的计算方式如下：

Ju,v|T=⎡⎣∂u∂rx∂v∂rx∂u∂ry∂v∂ry∂u∂rz∂v∂rz∂u∂tx∂v∂tx∂u∂ty∂v∂ty∂u∂tz∂v∂tz⎤⎦ J u , v | T = [ ∂ u ∂ r x ∂ u ∂ r y ∂ u ∂ r z ∂ u ∂ t x ∂ u ∂ t y ∂ u ∂ t z ∂ v ∂ r x ∂ v ∂ r y ∂ v ∂ r z ∂ v ∂ t x ∂ v ∂ t y ∂ v ∂ t z ]

其中，
∂u∂rx=ZXrx−XZrxZ2 ∂ u ∂ r x = Z X r x − X Z r x Z 2

v v 关于rx r x 的偏导数以此类推 Xrx X r x 表示的是 X X 在rx r x 方向上的偏导数， X,Y,Z X , Y , Z 为当前帧下的三维点坐标（即 X1c,Y1c,Z1c或X2c,Y2c,Z2c） X 1 c , Y 1 c , Z 1 c 或 X 2 c , Y 2 c , Z 2 c ） ，
通过上一帧的三维点以上述的公式计算可得，而其偏导数则通过下面的公式计算：

⎡⎣⎢XrxYrxZrx⎤⎦⎥=⎡⎣⎢⎢⎢⎢∂Xc∂rx∂Yc∂rx∂Zc∂rx⎤⎦⎥⎥⎥⎥=∂(R∗⎡⎣⎢⎢XpYpZp⎤⎦⎥⎥+⎡⎣⎢⎢txtytz⎤⎦⎥⎥)∂rx=∂R∂rx∗⎡⎣⎢XpYpZp⎤⎦⎥ [ X r x Y r x Z r x ] = [ ∂ X c ∂ r x ∂ Y c ∂ r x ∂ Z c ∂ r x ] = ∂ ( R ∗ [ X p Y p Z p ] + [ t x t y t z ] ) ∂ r x = ∂ R ∂ r x ∗ [ X p Y p Z p ]

ry,rz r y , r z 的偏导数以此类推，由上述关于 tx t x 偏导数的表达式，可得：

⎡⎣⎢XtxYtxZtx⎤⎦⎥=⎡⎣⎢100⎤⎦⎥ [ X t x Y t x Z t x ] = [ 1 0 0 ]

基于上述计算方式，可以算出抽样得到的三组点关于 (u1c,v1c) ( u 1 c , v 1 c ) 以及 (u2c,v2c) ( u 2 c , v 2 c ) 的雅可比矩阵（对于每一组来说，都用一个 4∗6 4 ∗ 6 的矩阵来表示）。接下来，还需要计算残差，供最优化 T T 使用
　　对于一组点，残差实质上就是(u,v) ( u , v ) 的观测值（匹配点坐标）与其重投影后的坐标的差值，再乘以权重：
　　
r=w∗[(u,v)−(u^,v^)] r = w ∗ [ ( u , v ) − ( u ^ , v ^ ) ]

乘上权重 w w 是为了减少标定参数不准确带来的误差，远离相机主点的特征点会赋予更低的权值，具体计算方式为：

w=cu|u−cu| w = c u | u − c u |

2.1.2 高斯牛顿迭代
在libviso的迭代过程中使用的高斯分布，实际上用了一个小技巧：将二次偏导数省略，只通过雅克比矩阵来进行迭代。通过计算三组点中的雅克比矩阵，最终，我们可以得到这样的一个矩阵：

J=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂u1c1∂rx∂u1c1∂ry∂u1c1∂rz∂u1c1∂tx∂u1c1∂ty∂u1c1∂tz∂v1c1∂rx∂v1c1∂ry∂v1c1∂rz∂v1c1∂tx∂v1c1∂ty∂v1c1∂tz∂u2c1∂rx∂u2c1∂ry∂u2c1∂rz∂u2c1∂tx∂u2c1∂ty∂u2c1∂tz∂v2c1∂rx∂v2c1∂ry∂v2c1∂rz∂v2c1∂tx∂v2c1∂ty∂v2c1∂tz⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ∂u1cN∂rx∂u1cN∂ry∂u1cN∂rz∂u1cN∂tx∂u1cN∂ty∂u1cN∂tz∂v1cN∂rx∂v1cN∂ry∂v1cN∂rz∂v1cN∂tx∂v1cN∂ty∂v1cN∂tz∂u2cN∂rx∂u2cN∂ry∂u2cN∂rz∂u2cN∂tx∂u2cN∂ty∂u2cN∂tz∂v2cN∂rx∂v2cN∂ry∂v2cN∂rz∂v2cN∂tx∂v2cN∂ty∂v2cN∂tz⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥ J = [ ∂ u 1 c 1 ∂ r x ∂ v 1 c 1 ∂ r x ∂ u 2 c 1 ∂ r x ∂ v 2 c 1 ∂ r x ⋯   ∂ u 1 c N ∂ r x ∂ v 1 c N ∂ r x ∂ u 2 c N ∂ r x ∂ v 2 c N ∂ r x ∂ u 1 c 1 ∂ r y ∂ v 1 c 1 ∂ r y ∂ u 2 c 1 ∂ r y ∂ v 2 c 1 ∂ r y ⋯   ∂ u 1 c N ∂ r y ∂ v 1 c N ∂ r y ∂ u 2 c N ∂ r y ∂ v 2 c N ∂ r y ∂ u 1 c 1 ∂ r z ∂ v 1 c 1 ∂ r z ∂ u 2 c 1 ∂ r z ∂ v 2 c 1 ∂ r z ⋯   ∂ u 1 c N ∂ r z ∂ v 1 c N ∂ r z ∂ u 2 c N ∂ r z ∂ v 2 c N ∂ r z ∂ u 1 c 1 ∂ t x ∂ v 1 c 1 ∂ t x ∂ u 2 c 1 ∂ t x ∂ v 2 c 1 ∂ t x ⋯   ∂ u 1 c N ∂ t x ∂ v 1 c N ∂ t x ∂ u 2 c N ∂ t x ∂ v 2 c N ∂ t x ∂ u 1 c 1 ∂ t y ∂ v 1 c 1 ∂ t y ∂ u 2 c 1 ∂ t y ∂ v 2 c 1 ∂ t y ⋯   ∂ u 1 c N ∂ t y ∂ v 1 c N ∂ t y ∂ u 2 c N ∂ t y ∂ v 2 c N ∂ t y ∂ u 1 c 1 ∂ t z ∂ v 1 c 1 ∂ t z ∂ u 2 c 1 ∂ t z ∂ v 2 c 1 ∂ t z ⋯   ∂ u 1 c N ∂ t z ∂ v 1 c N ∂ t z ∂ u 2 c N ∂ t z ∂ v 2 c N ∂ t z ]

N N 为抽样的点个数（3） （ 3 ） ,令
A=JJT A = J J T
b⃗ =Jr b ⃗ = J r ⃗
,其中 r r ⃗ 为残差组成的向量：

r⃗ =⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢r1c1r2c1r1c2⋮r1cNr2cN⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥ r → = [ r 1 c 1 r 2 c 1 r 1 c 2 ⋮ r 1 c N r 2 c N ]

最后，高斯牛顿法通过下面的公式，进行 T T 的迭代：

T(i+1)=T(i)+A−1r⃗  T ( i + 1 ) = T ( i ) + A − 1 r →

往复迭代，直到 T T 收敛

|T(i+1)−T(i)|<ε | T ( i + 1 ) − T ( i ) | < ε

2.2 最优位姿选取

从匹配点中选取3个，并通过高斯牛顿法，求出位姿 T T ，即完成了一次RANSAC R A N S A C 迭代。然而，每次迭代之后，我们都要判断计算出来的T的精确度。在libviso中，精确度是通过局内点 (inlier) ( i n l i e r ) 的个数来衡量的，若通过当前的位姿 T T

求得的局内点更多，就将这个位姿替换成当前最好的位姿。

　　局内点的计算方式如下：先计算出(u^,v^) ( u ^ , v ^ ) ,随后，满足下式的点即为局内点：
　　
　　 ∑i∈1c,2c(ui^−ui)2+(vi^−vi)2<t ∑ i ∈ 1 c , 2 c ( u i ^ − u i ) 2 + ( v i ^ − v i ) 2 < t
　　
　其中 t t 为人为设定的参数。
　经过多次RANSAC R A N S A C 迭代，最终能够快速鲁棒地找到两帧之间的位姿变换。这里的位姿变换是通过 T T
来表征的，而最终需要换算到R|t R | t 矩阵，所需要的公式在此不再赘述。

3 小结

本文详细地描述了在libviso中用到的位姿求解的过程。其主要思路是利用随机抽样，每次从匹配点中取出3组，进行高斯牛顿迭代，求出基于这3组点的位姿，再通过内点判断这个位姿的精确度，多次抽样——迭代后，得到一个准确的位姿。抽样能够能够加快高斯牛顿法的收敛速度，而RANSAC的思路则保证了这种抽样的鲁棒性，降低了动态点对算法的影响，是一种值得借鉴的思路。

libviso的project主页位于
http://www.cvlibs.net/software/libviso/
,另外，我将其中的位姿求解模块单独抽取出来，供读者参考：
https://github.com/RichardChe/libviso_pose_estimation