数学建模之综合评价模型（层次分析法+Topsis法+熵权法）

以下内容均听自清风老师的建模教程 （老师讲的很好哦，大家可以去听听，结合实例不枯燥！）

一，层次分析法

以一道例题进行分析：

小明同学想出去旅游，在查阅了网上的攻略后，他初步选择了苏杭，北戴河，桂林三个地方

请你确定评价指标，形成评价体系为小明同学选择最佳的方案。

第一步：确定模型

题中出现“确定评价指标，形成评价体系”这类词眼，确定这是一道层次分析题。

第二步：建立层次结构模型

我们从三个问题入手：

        1.我们评价的目标是什么？

                答：为小明选择最佳的旅游景点。

        2.我们为了达到这个目标有哪几种可选的方案？

                答：三种。分别是去苏杭，去北戴河，去桂林。

        3.评价的准则或者说指标是什么？

                答：景色，花费，居住，饮食，交通。

第三个的答案我们可以根据题目中的背景材料，常识，以及网上（知网，百度学术，虫部落-快搜）搜索到的参考资料进行结合，从中筛选合适的指标

第三步：构建权重表格

我们最终的目标就是要填满这个权重矩阵！！！（同颜色的单元格和为1）

                                                                重要性表

（1）构建指标之间的判断矩阵：两个指标两个指标进行比较，根据重要性表填写两两比较的结果

1.比较景色和花费的重要程度

        答：花费比景色略微重要（景色：花费 = 1：2）

2.比较景色和居住的重要程度

        答：景色比居住要重要一点（景色：居住 = 4 ：1）

…………

总共需要比较次

判断矩阵：

 上面的矩阵就是层次分析法中的正互反矩阵（我们需要知道正互反矩阵的特点）

        （1）aij表示：与 j 相比，i 的重要程度（例如：和居住相比，景色的重要程度是4）

        （2）当 i = j 时，两个指标相同，同等重要记为1

        （3）aij > 0 && aij x aji = 1

（2）构建每个指标下，方案之间的判断矩阵

1.比较苏杭的花费和北戴河的花费的多少程度

        答：北戴河的花销要比苏杭的花销要稍多（北戴河：苏杭 = 3 ：1）

2.比较苏杭的花费和桂林的花费的多少程度

        答：桂林的花销要比苏杭的花销要贵的多得多（桂林：苏杭 = 8 ：1）

3.比较北戴河的花花费和桂林的花费的多少程度

        答：桂林的花销要比北戴河要稍多（桂林 ： 北戴河 = 3 ：1）

……

判断矩阵：

第四步：对判断矩阵一致性检验 （如果判断矩阵已经是一致矩阵，那么就没必要进行一致性检验）

首先介绍一下一致矩阵：

        在判断矩阵的前提下，如果各行成比例且各列成比例，那么该矩阵就是一致矩阵

        第一步：计算判断矩阵的最大特征值及一致性指标CI

                                         

         第二步：根据n的大小，按照下表查找平均随机一致性指标RI，计算一致性比例CR

        第三步：判断判断矩阵的一致性是否小于0.1

结论：如果CR < 0.1, 则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正。修正的方法：往一致矩阵上去凑（各行各列成比例  ）

第五步：计算判断矩阵的权重（算术平均法，几何平均法，特征值法三种最好都用上）

（1）算术平均法求权重

        第一步：将判断矩阵按照列归一化（每个元素除以其所在列的和)

        第二步：将归一化的各列相加（按行求和）

        ​​​​​第三步：将相加后得到的向量中的每个元素除以n即可得到权重向量

（2）几何平均法求权重

        第一步：将判断矩阵按行相乘得到一个新的列向量

        第二步：将该列向量中的每个元素开n方

        第三步：对开方后的列向量进行归一化处理（列向量中的每个元素除以该列的和）

（3）特征值法求权重

        第一步：求出矩阵的最大特征值以及对应的特征向量

        第二步：对最大特征值对应的的特征向量进行归一化处理即可得到我们的权重  

第六步：构建最终的权重表，将特征值法计算出的结果填入对应的颜色项中

第七步：计算得分

苏杭得分 = 0.2636*0.5954 + 0.4758*0.0819 + 0.0538*0.4286 + 0.0981*0.6337 + 0.1087*0.1667 = 0.29926

……

用excel进行计算：

B这一列一定要锁住（shift+f4），计算的才是正确的

结果：

二，Topsis模型（优劣距离法）

还是以一道例题为例：

 已知：25条河流水质量各指标的数据，其中含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10~20之间最佳。请评价下列20条河流的水质情况

第一步:将原始矩阵正向化处理（将所有的指标类型统一转换为极大型指标）

四种最常见的指标分类：

极小型指标——>极大型指标的公式：

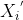         = max{，……}-

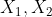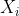
中间型指标——>极大型指标的公式：

设{}是一组中间型指标序列，最佳的数值是，那么

        M = max{||}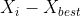

         =  

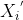区间型指标——>极大型指标的公式：

设{}是一组区间型指标序列，最佳的区间是【a,b】，那么

        M = max{a-min{Xi}，max{Xi}-b} 

       

 第二步：对正向化后的矩阵进行标准化处理（消除不同量纲之间的影响）

假设有n个评价对象，m个评价指标的正向化矩阵如下:

将标准化矩阵记为Z，(每一个元素 / 其所在列的元素平方和再开方) 

第三步：计算得分并归一化处理

假设有n个评价对象，m个评价指标的标准化矩阵如下:

Zij表示第i个同学的第j个指标

最大值 = max{,,……，}

                 = max{max{,,……}，……，max{,,……}}

最小值= min{,,……，}

                = min{min{,,……}，……，min{,,……}}

第 i (i=1，2，3，……，n)个评价对象与最大值的距离： = 

第 i(i=1，2，3，……，n）个评价对象与最小值的距离：=

那么，我们就可以得出第i个评价对象未归一化处理的得分：

(越小，Si越接近最大值1)

然后对得分进行归一化处理（这一列的每个元素除以该列元素总和），得到第i个评价对象的最终得分。

基于熵权法的Topsis模型

依据的原理：指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。（例如：对于所有的样本，这个指标都是相同的数值，那么我们可认为这个指标的权值为0，即这个指标对于我们的评价不起任何帮助）

如何衡量信息量的大小：

越有可能发生的事（概率越大），信息量越少

越不可能发生的事（概率越小），信息量越大

所以，我们可以用概率来衡量信息量的大小

假设x表示事件X可能发生的某种情况，p(x)表示这种情况发生的概率

他们之间的关系是：I(x) = -ln(p(x))，因为0<=p(x)<=1，所以I(x)>=0

如果事件X可能发生的情况分别为x1,x2,……，xn，那么我们可以定义事件X的信息熵(对信息量的期望值)为：

     

 定理：当p(x1) = p(x2) = …… = p(xn) = 时，H(X)取最大值，最大值为Inn

第一步和第二步和上述的Topsis法一样

第三步：如果标准化后的矩阵中存在负数，则需要对正向化矩阵X实行另一种标准化的方法，其公式为：

         

这样标准化后的矩阵就能将每个值囊括在[0,1]之间

第四步：计算概率矩阵，即计算第j个指标下第i个样本所占的比重

第五步：计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权

对于第j个指标而言，计算信息熵的公式为：

                                信息效用值的公式为:

之后，对信息效用值进行归一化处理，就能得到每个指标的权重：

第六步：计算得分并归一化处理（和Topsis的第三步略有不同！！！）

假设有n个评价对象，m个评价指标的标准化矩阵如下:

Zij表示第i个同学的第j个指标

最大值 = max{,,……，}

                 = max{max{,,……}，……，max{,,……}}

最小值= min{,,……，}

                = min{min{,,……}，……，min{,,……}}

第 i (i=1，2，3，……，n)个评价对象与最大值的距离：

第 i(i=1，2，3，……，n）个评价对象与最小值的距离：

那么，我们就可以得出第i个评价对象未归一化处理的得分：

(越小，Si越接近最大值1)

然后对得分进行归一化处理（这一列的每个元素除以该列元素总和），然后得到第i个评价对象的最终得分。

在写代码中可能会出现的两个问题：

1.你可能导入数据集类型错误，重新导入数据集并在导入时更改类型为数值矩阵（原本为table）

2.如果出现未定义Positivization()的情况，请将该函数所在文件夹路径复制粘贴到matlab中，将其变为当前文件夹！！！