【拓扑学知识】1.拓扑空间与度量拓扑
没错,这个系列是我无法安心复习而使用记博客的方式来对拓扑学知识重点(考点)进行汇总总结。以尤承业老师的《基础拓扑学讲义》为基础。
第一节首先引入拓扑空间、度量空间等基础概念。
文章目录
- 0.前置知识(幂集和子集族)
-
- 幂集和子集族
- 1.拓扑空间
-
- 1.1 拓扑空间定义
- 1.2 闭集
- 1.3 “特殊”的拓扑
- 2.度量拓扑
-
- 2.1 度量空间的定义
- 2.2 度量拓扑
- 3.子空间
- 4.拓扑空间的几个基本概念
-
- 4.1 邻域、内点与内部
- 4.2 聚点与闭包
- 4.3 稠密与可分拓扑空间
- 4.4 序列收敛
0.前置知识(幂集和子集族)
幂集和子集族
设 X X X为非空集合,记 2 X 2^X 2X是 X X X的全体子集(包含 X X X及空集 ∅ \varnothing ∅)的集合,称为 X X X的幂集。把 2 X 2^X 2X的子集(即以 X X X的一部分子集为成员的集合)称为 X X X的子集族。
1.拓扑空间
1.1 拓扑空间定义
设 X X X为一非空集合, X X X的一个子集族 τ \tau τ称为 X X X的一个拓扑,如果它满足下列三条拓扑公理:
(1) X , ∅ X,\varnothing X,∅都包含在 τ \tau τ中。
(2) τ \tau τ中任意个成员的并集仍在 τ \tau τ中。
(3) τ \tau τ中有限个成员的交集仍在 τ \tau τ中。
( 3 ′ 3' 3′)(3)的等价表述: τ \tau τ中两个成员的交集仍在 τ \tau τ中。
集合 X X X和它的一个拓扑 τ \tau τ一起称为一个拓扑空间,记作 ( X , τ ) (X,\tau) (X,τ),称 τ \tau τ中的成员为这个拓扑空间的开集。
所以拓扑的实质是 X X X的一个满足拓扑公理的子集族。给出集合的一个拓扑,就是规定它的哪些子集是开集。这种规定不是任意的,其必须满足三条拓扑公理。但一般来说,一个集合上可以规定许多不同的拓扑,因此说到一个拓扑空间时,要同时指明集合及所规定的拓扑,也常常只用集合来称呼一个拓扑空间,如拓扑空间 X X X等。
即然有了开集,那我们是是不是要说一下 “闭集” 酱呢。
1.2 闭集
(1)闭集的定义: 拓扑空间 X X X的一个子集A称为闭集,如果 A c A^c Ac是开集。(开集的余集)
eg: X X X的离散拓扑 2 X 2^X 2X,任何子集都是开集,从而任何子集也都是闭集。
(2)闭集的3个重要性质:
one: X X X与 ∅ \varnothing ∅都是闭集。
因为 ∅ , X \varnothing,X ∅,X必定为开集,而她们的补集又是彼此,所以对于任何拓扑空间 ∅ , X \varnothing,X ∅,X必定为闭集。
two:任意多个闭集的交集是闭集。
three:有限多个闭集的并集是闭集。
为说明two和Three,这里先介绍一个重要的集合运算定律:摩根定律(De Morgan公式)
B \ ⋃ λ ∈ Λ A λ = ⋂ λ ∈ Λ ( B \ A λ ) , (1) B\backslash\bigcup_{\lambda \in \Lambda}A_\lambda = \bigcap_{\lambda \in \Lambda}(B\backslash A_\lambda),\tag{1} B\λ∈Λ⋃Aλ=λ∈Λ⋂(B\Aλ),(1)
B \ ⋂ λ ∈ Λ A λ = ⋃ λ ∈ Λ ( B \ A λ ) (2) B\backslash\bigcap_{\lambda \in \Lambda}A_\lambda = \bigcup_{\lambda \in \Lambda}(B\backslash A_\lambda) \tag{2} B\λ∈Λ⋂Aλ=λ∈Λ⋃(B\Aλ)(2)
把 B B B换称全集, ( B \ A λ ) = ( A λ ) c (B\backslash A_\lambda)=(A_\lambda)^c (B\Aλ)=(Aλ)c
这个摩根定律在拓扑,概率论,实变函数都常常用到,需要牢记。
所以由摩根定律和拓扑公理(2)(3)知,two和three成立。
1.3 “特殊”的拓扑
“最大”与“最小”的拓扑。
(1)离散拓扑:设 X X X为一非空集合,显然 X X X的幂集 2 X 2^X 2X构成 X X X的拓扑 τ s \tau_s τs,称为 X X X上的离散拓扑。
显然 X X X的任意拓扑 τ ⊂ τ s \tau \subset \tau_s τ⊂τs。
(2)平凡拓扑:{ X , ∅ X,\varnothing X,∅}也是 X X X上的拓扑,称为 X X X上的平凡拓扑 τ t \tau_t τt。
同样,对于 X X X的任意拓扑 τ \tau τ,有 τ t ⊂ τ \tau_t \subset \tau τt⊂τ。
"大白话”拓扑
(3)余有限拓扑:设 X X X是无穷集合, τ f \tau_f τf={ A c A^c Ac | A A A是 X X X的有限子集} ⋃ \bigcup ⋃{ ∅ \varnothing ∅},不难验证 τ f \tau_f τf是 X X X的一个拓扑,称为 X X X上的余有限拓扑。
(4)余可数拓扑:设 X X X是无穷集合, τ c \tau_c τc={ A c A^c Ac | A A A是 X X X的可数子集} ⋃ \bigcup ⋃{ ∅ \varnothing ∅},不难验证 τ c \tau_c τc是 X X X的一个拓扑,称为 X X X上的余可数拓扑。
(5)欧式拓扑:设R是全体实数的集合,规定 τ e \tau_e τe={ U U U | U U U是若个开区间的并集},这里 “若干个” 可以是无穷,有限,也可以是0,因此 ∅ ∈ τ e \varnothing\in \tau_e ∅∈τe,进一步可以验证 τ e \tau_e τe是R上的拓扑,称为R上的欧式拓扑,记为 E 1 = ( R , τ e ) E^1=(R,\tau_e) E1=(R,τe)。
(记住这个”若干个“,)
既然都叫拓扑“空间"了,那怎么能少了“度量”呢(叉腰)
2.度量拓扑
2.1 度量空间的定义
集合 X X X的一个度量 d d d是一个映射, d : X × X → R d:X\times X\rightarrow R d:X×X→R,它满足:
(1)正定性: d ( x , x ) = 0 , ∀ x ∈ X d ( x , y ) > 0 d(x,x)=0,\forall x\in X \\d(x,y)>0 d(x,x)=0,∀x∈Xd(x,y)>0,当 x ≠ y x\not=y x=y时;
(2)对称性: d ( x , y ) = d ( y , x ) , ∀ x , y ∈ X d(x,y)=d(y,x),\forall x,y\in X d(x,y)=d(y,x),∀x,y∈X;
(3)三角不等式:
d ( x , z ) ≤ d ( x , y ) + d ( y , z ) , ∀ x , y , z ∈ X d(x,z)\leq d(x,y)+d(y,z),\forall x,y,z\in X d(x,z)≤d(x,y)+d(y,z),∀x,y,z∈X
当集合 X X X规定一个度量 d d d后,称为度量空间,记作 ( X , d ) (X,d) (X,d)。
eg:n维欧式空间
记 R n = R^n= Rn={ ( x 1 , x 2 , . . . , x n ) ∣ x i ∈ R , i = 1 , . . . , n (x_1,x_2,...,x_n) | x_i\in R,i=1,...,n (x1,x2,...,xn)∣xi∈R,i=1,...,n}。规定 R n R^n Rn上的度量 d d d为:
d ( ( x 1 , x 2 , . . . , x n ) , ( y 1 , y 2 , . . . , y n ) ) = ∑ i = 1 n ( x i − y i ) 2 , d((x_1,x_2,...,x_n),(y_1,y_2,...,y_n))=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}, d((x1,x2,...,xn),(y1,y2,...,yn))=i=1∑n(xi−yi)2,
不难验证 d d d满足正定性、对称性和三角不等式。记 E n = ( R n , d ) E^n=(R^n,d) En=(Rn,d),称为n维欧氏空间。
那么有了度量空间,怎样生成一个拓扑呢?或者说“度量拓扑”到底是什么呢?
2.2 度量拓扑
设 ( X , d ) (X,d) (X,d)是一个度量空间,下面规定 X X X的一个拓扑。
首先介绍球形域的概念,这是我们寻找拓扑的基础。
(1)球形领域:设 x 0 ∈ X , ϵ x_0\in X,\epsilon x0∈X,ϵ是一正数,称 X X X的子集:
B ( x 0 , ϵ ) : = { x ∈ X ∣ d ( x 0 , x ) < ϵ } B(x_0,\epsilon):=\lbrace x\in X| d(x_0,x)<\epsilon \rbrace B(x0,ϵ):={x∈X∣d(x0,x)<ϵ}
为以 x 0 x_0 x0为球心, ϵ \epsilon ϵ为半径的球形邻域。
(2)引理: ( X , d ) (X,d) (X,d)的任意两个球形领域的交集是若干个球形领域的并集。
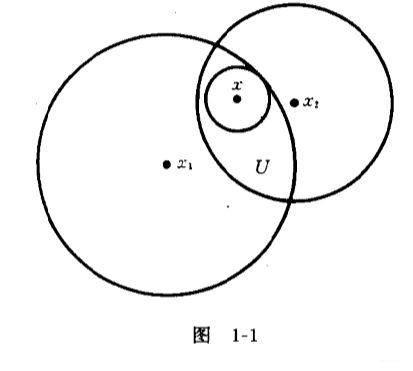
证明:设 U = B ( x 1 , ϵ 1 ) ⋂ B ( x 2 , ϵ 2 ) U=B(x_1,\epsilon_1) \bigcap B(x_2,\epsilon_2) U=B(x1,ϵ1)⋂B(x2,ϵ2), ∀ x ∈ U \forall x\in U ∀x∈U,则 ϵ i − d ( x , x i ) > 0 ( i = 1 , 2 ) \epsilon_i-d(x,x_i)>0(i=1,2) ϵi−d(x,xi)>0(i=1,2)(看图1-1)。记 ϵ x = m i n { ϵ 1 − d ( x , x 1 ) , ϵ 2 − d ( x , x 2 ) } \epsilon_x=min\lbrace \epsilon_1-d(x,x_1),\epsilon_2-d(x,x_2) \rbrace ϵx=min{ϵ1−d(x,x1),ϵ2−d(x,x2)},不难验证 B ( x , ϵ x ) ⊂ U B(x,\epsilon_x) \subset U B(x,ϵx)⊂U,于是 U = ⋃ x ∈ U B ( x , ϵ x ) . U=\bigcup_{x \in U}B(x,\epsilon_x). U=⋃x∈UB(x,ϵx).
规定 X X X的子集族 τ d = { U ∣ U \tau_d=\lbrace U| U τd={U∣U是若干个球形领域的并集 } \rbrace }
命题:实际上 τ d \tau_d τd就是我们要的度量空间的一个拓扑。
证明:
验证拓扑公理(1)
因为:0个球形邻域的并集即 ∅ \varnothing ∅("若干个”),所以 ∅ ∈ τ d \varnothing \in \tau_d ∅∈τd;因为 X X X可以由若干个球形邻域的并产生,因此 X ∈ τ d X \in \tau_d X∈τd。所以 ∅ , X ∈ τ d \varnothing,X \in \tau_d ∅,X∈τd, 即 τ d \tau_d τd满足拓扑公理(1)。
验证拓扑公理(2)
因为“若干”可以是无穷,所以 τ d \tau_d τd任意成员的并仍在 τ d \tau_d τd中,即 τ d \tau_d τd满足拓扑公理(2)。
验证拓扑公理(3)
只需要验证 τ d \tau_d τd中两个成员的交集仍在 τ d \tau_d τd中即可。
设 U , U ′ ∈ τ d U,U' \in \tau_d U,U′∈τd,记 U = ⋃ α B ( x α , ϵ α ) U=\bigcup_{\alpha} B(x_\alpha, \epsilon_\alpha) U=⋃αB(xα,ϵα), U ′ = ⋃ β B ( x β ′ , ϵ β ′ ) U'=\bigcup_{\beta} B(x'_\beta, \epsilon'_\beta) U′=⋃βB(xβ′,ϵβ′)。
则 U ⋂ U ′ = ( ⋃ α B ( x α , ϵ α ) ) ⋂ ( ⋃ β B ( x β ′ , ϵ β ′ ) ) = ⋃ α , β ( B ( x α , ϵ α ) ⋂ B ( x β ′ , ϵ β ′ ) ) U \bigcap U'=(\bigcup_{\alpha} B(x_\alpha, \epsilon_\alpha)) \bigcap (\bigcup_{\beta} B(x'_\beta, \epsilon'_\beta))=\bigcup_{\alpha,\beta}(B(x_\alpha, \epsilon_\alpha) \bigcap B(x'_\beta, \epsilon'_\beta)) U⋂U′=(⋃αB(xα,ϵα))⋂(⋃βB(xβ′,ϵβ′))=⋃α,β(B(xα,ϵα)⋂B(xβ′,ϵβ′))
(“引理”来点作用8。)
由引理知,任意两个球形领域的交集是若干个球形邻域的闭集。
所以对于 ∀ α , β , B ( x α , ϵ α ) ⋂ B ( x β ′ , ϵ β ′ ) ∈ τ d \forall \alpha,\beta,B(x_\alpha, \epsilon_\alpha) \bigcap B(x'_\beta, \epsilon'_\beta) \in \tau_d ∀α,β,B(xα,ϵα)⋂B(xβ′,ϵβ′)∈τd,再同理拓扑公理(2)得 U ⋂ U ′ = ⋃ α , β ( B ( x α , ϵ α ) ⋂ B ( x β ′ , ϵ β ′ ) ) ∈ τ d U \bigcap U'=\bigcup_{\alpha,\beta}(B(x_\alpha, \epsilon_\alpha) \bigcap B(x'_\beta, \epsilon'_\beta)) \in \tau_d U⋂U′=⋃α,β(B(xα,ϵα)⋂B(xβ′,ϵβ′))∈τd。即 τ d \tau_d τd中两个成员的交集仍在 τ d \tau_d τd, τ d \tau_d τd满足拓扑公理(3)。
(3)度量拓扑:由上面的证明知: τ d = { U ∣ U \tau_d=\lbrace U| U τd={U∣U是若干个球形领域的并集 } \rbrace }是 X X X上的一个拓扑。称 τ d \tau_d τd为 X X X上由度量 d d d决定的度量拓扑。
因此每个度量空间都能自然地看成具有度量拓扑的拓扑空间。或者给定一个集合 X X X,规定其度量 d d d后,就能自然有度量空间,有度量拓扑。
有了拓扑空间,再来看看她的子空间。
3.子空间
定义:
设A是拓扑空间 ( X , τ ) (X,\tau) (X,τ)的一个非空子集。规定A的子集族:
τ A : = { U ⋂ A ∣ U ∈ τ } \tau_A:=\lbrace U \bigcap A| U\in \tau \rbrace τA:={U⋂A∣U∈τ}容易验证 τ A \tau_A τA是A上的一个拓扑( τ \tau τ是X上的拓扑),称为 τ \tau τ导出的A上的子空间拓扑,称 ( A , τ A ) (A,\tau_A) (A,τA)为 ( X , τ ) (X,\tau) (X,τ)的子空间。
以后拓扑空间的子集都将看作拓扑空间,即子空间。
一个重要的命题(结论)
设X是拓扑空间, C ⊂ A ⊂ X C \subset A \subset X C⊂A⊂X,则C是A的闭集 ⟺ \iff ⟺C是A与X的一个闭集之交集。
既然上面刻画了球形领域,那么邻域怎么能少。说到邻域,内点,聚点,闭包什么的,拓扑空间会不会与数分所学的有所差异?下面将以以介绍。
4.拓扑空间的几个基本概念
既然拓扑是规定了哪些子集是开集,那么下面的概念基本都是以集合语言刻画的。
4.1 邻域、内点与内部
(1)定义:设 A A A是拓扑空间 X X X的一个子集,点 x ∈ A x \in A x∈A。如果存在开集 U U U,使得 x ∈ U ⊂ A x \in U \subset A x∈U⊂A,则称 x x x是A的一个内点,A是 x x x的一个邻域。A的所有内点的集合称为A的内部,记做 A 。 A^。 A。
(2)常用性质
one:若 A ⊂ B A \subset B A⊂B,则 A 。 ⊂ B 。 A^。\subset B^。 A。⊂B。;
two: A 。 A^。 A。是包含在A中的所有开集的并集,因此是包含在A中的最大开集。
three: A 。 = A ⟺ A^。=A \iff A。=A⟺A是开集;
four: ( A ⋂ B ) 。 = A 。 ⋂ B 。 (A \bigcap B)^。= A^。\bigcap B^。 (A⋂B)。=A。⋂B。
five: ( A ⋃ B ) 。 ⊃ A 。 ⋃ B 。 (A \bigcup B)^。\supset A^。\bigcup B^。 (A⋃B)。⊃A。⋃B。
4.2 聚点与闭包
啊这,这个是真的很重要,证明老出了,还跟数分上差别较大。
(1)定义:设A是拓扑空间 X X X的子集。 x ∈ X x \in X x∈X,如果 x x x的每个邻域都含有 A \ { x } A \backslash \lbrace x \rbrace A\{x}中的点,则称 x x x为A的聚点。A的所有聚点的集合称为A的导集,记做 A ′ A' A′。称集合 A ‾ : = A ⋃ A ′ \overline{A}:=A \bigcup A' A:=A⋃A′为A的闭包。
由定义不难推出: x ∈ A ‾ ⟺ x \in \overline{A} \iff x∈A⟺ x x x的任一邻域与A都有交点。
这里要注意, x x x是 ∈ X \in X ∈X的,所以它的每个邻域 U U U是 ⊂ X \subset X ⊂X的而非 ⊂ A \subset A ⊂A。
eg: 设 X = { a , b , c } X=\lbrace a,b,c \rbrace X={a,b,c},规定拓扑 τ = { X , ∅ , { a } } \tau = \lbrace X,\varnothing,\lbrace a \rbrace \rbrace τ={X,∅,{a}},则当 A = { a } A = \lbrace a \rbrace A={a}时, x = b , c x=b,c x=b,c,其邻域为 U = X U=X U=X,而 U \ x U\backslash x U\x显然含 a a a,即 x = b , c x=b,c x=b,c每个邻域 U ⋂ A \ { x } ≠ ∅ U \bigcap A\backslash \lbrace x \rbrace \not= \varnothing U⋂A\{x}=∅,即 x x x的每个邻域均含有 A \ { x } A\backslash \lbrace x \rbrace A\{x}的点,故 x = b , c x=b,c x=b,c为 A = { a } A=\lbrace a \rbrace A={a}的聚点。
(2)常用性质:
one:若 A ⊂ B A \subset B A⊂B,则 A ‾ ⊂ B ‾ \overline{A} \subset \overline{B} A⊂B;
two: A ‾ \overline{A} A是所有包含A闭集的交集,所以是包含A的最小的闭集;
three: A ‾ = A ⟺ \overline{A}=A \iff A=A⟺A是闭集;
four: A ⋃ B ‾ = A ‾ ⋃ B ‾ \overline{A \bigcup B} = \overline{A} \bigcup \overline{B} A⋃B=A⋃B;
five:: A ⋂ B ‾ ⊂ A ‾ ⋂ B ‾ \overline{A \bigcap B} \subset \overline{A} \bigcap \overline{B} A⋂B⊂A⋂B;
这里给出two的证明:设 { U β ∣ β ∈ λ } \lbrace U_{\beta}|\beta\in \lambda \rbrace {Uβ∣β∈λ}是包含A的所有闭集构成的子集族。
4.3 稠密与可分拓扑空间
如果拓扑空间X的子集A,满足 A ‾ = X \overline{A}=X A=X,则称A是稠密的。如果X有可数的稠密子集,则称X是可分拓扑空间。

( R , τ f (R,\tau_f (R,τf)为余有限拓扑, ( R , τ c ) (R,\tau_{c}) (R,τc)为余可数拓扑
4.4 序列收敛
这个我们只要了解其定义即可。
设 { x n } \lbrace x_n \rbrace {xn}是拓扑空间 X X X中点的序列,如果点 x 0 ∈ X x_0 \in X x0∈X的任一邻域U都包含 { x n } \lbrace x_n \rbrace {xn}的几乎所有项(即只有有限个 x n x_n xn不在U中;或者说存在正整数N,使得当 n > N n > N n>N时, x n ∈ U x_n \in U xn∈U,则说 { x n } \lbrace x_n \rbrace {xn}收敛到 x 0 x_0 x0,记做 x n → x 0 x_n\rightarrow x_0 xn→x0。
要注意的是与数分不一样的地方,序列可能收敛到多个点。
例如 ( R , τ f ) (R,\tau_f) (R,τf)中,只要 { x n } \lbrace x_n \rbrace {xn}的项两两不同,则任一点 x ∈ R x \in R x∈R的邻域(有限集的余集)包含 { x n } \lbrace x_n \rbrace {xn}的几乎所有项,从而 x n → x x_n\rightarrow x xn→x。
