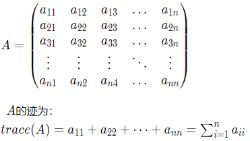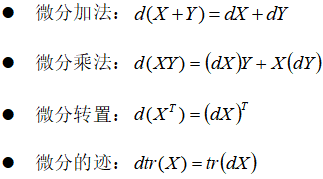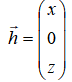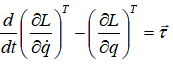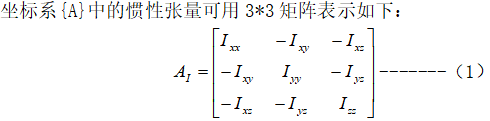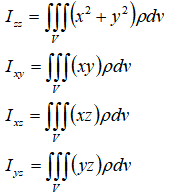(8)机器人动力学

目录

一、相关数学内容：

1、迹：

2、反对称矩阵：

3、矩阵微分和迹的性质：

二、质点动力学：

1、牛顿第二定律：

2、质点的能量：

 3、质点动力学的拉格朗日推导：

三、单刚体动力学：

1、转动惯量：

2、惯性矩：

3、惯性积：

 4、惯性张量：

 5、牛顿方程：

6、欧拉方程：

7、刚体动力学：

---

（说明：博客中的很多内容都是学习笔记的整理和记录，非原创，如有涉及侵权请联系删除，谢谢。）

机器人是一个具有多输入多输出的复杂动力学系统，存在严重的非线性，需要非常系统的方法对机器人进行动力学研究。常用的机器人动力学建模方法有：Lagrange（拉格朗日）动力学方法、Newton-Euler（牛顿-欧拉）动力学方法、Gauss（高斯）动力学方法、Kane（凯恩）动力学方法等。

机器人动力学研究的是机器人的运动和作用力之间的关系。机器人的动力学问题包括动力学正问题和动力学逆问题。动力学正问题是对于给定的关节驱动力/力矩，求解机器人对应的运动。需要求解非线性微分方程组，计算复杂，主要用于机器人的运动仿真。动力学逆问题是已知机器人的运动，计算对应的关节驱动力/力矩，即计算实现预定运动需要施加的力/力矩。不需要求解非线性方程组，计算相对简单，主要用于机器人的运动控制。

机器人动力学的用途主要有一下三个方面：

①、为机器人设计提供依据：能计算出实现预定运动所需的力/力矩；

②、机器人的动力学仿真：能根据连杆质量、负载、传动结构进行动态性能仿真；

③、实现机器人的最优控制：能优化性能指标和动态性能，调整伺服增益；

这里主要介绍利用Lagrange（拉格朗日）动力学方法、Newton-Euler（牛顿-欧拉）动力学方法去建立机械臂的动力学模型。

为了能更好的理解这些内容，这里先介绍一些基础内容点：

一、相关数学内容：

1、迹：

在线性代数中一个方阵的对角元素之和称为迹。

 迹是方阵的一个非常重要的特征：①相似矩阵的迹相同；②迹是矩阵的特征值之和；

2、反对称矩阵：

我们把满足的n阶方阵A称为反对称矩阵；若A是反对称矩阵，则根据定义有如果则可以得到，说明反对称矩阵的一个性质即主对角线上的元素为0。

 在matlab中skew()命令可以将一个向量（一维或三维）变成一个反对称矩阵如下：

 

 利用反对称矩阵可以实现将两个向量的叉积变为矩阵与向量的点积。

 

则： 。

3、矩阵微分和迹的性质：

 

二、质点动力学：

为了研究机器人的动力学，先要了解一下质点动力学，然后是单刚体动力学，最后多刚体动力学，这样一个由浅入深的过程是比较好的。

1、牛顿第二定律：

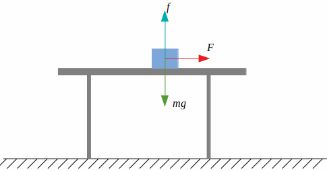
质点动力学方程最为简单和直观它就是牛顿第二定律：合外力等于质量乘以加速度。如下图所示在光滑桌面上有个滑块在运动。

 先来做一下受力分析，滑块受到重力mg，与重力平衡的支持力f，水平方向的推力F。由于桌面光滑，没有摩擦力。因此滑块的合外力为F，选择向右和向上为正方向，那么根据牛顿第二定律有：

 这个就是质点的动力学方程了。

2、质点的能量：

对于运动的质点包含了两部分的能量即动能和势能。势能定义为：

 这里采用建立坐标系加矢量运算的方式来求解势能，建立如下图所示坐标系：

 

 

 

 然后定义：

可知L是一个标量，这个方程就是拉格朗日函数，对质点而言拉格朗日的形式是非常简洁的。

 3、质点动力学的拉格朗日推导：

前面以及得到了质点的拉格朗日函数，下面给出机器人学中的拉格朗日方程定义如下：

 

 

 可以看出，这一项的结果对应的质点的重力。因此对于质点而言它的拉格朗日方程实际上是：

 我们知道合外力是指质点所受到的所有力（包括重力、支持力、推力）的合力。那么合外力减去重力是什么呢？其实就是除了重力以外所有力（包括支持力、推力，如果桌面不光滑还会有摩擦力）的合力。西西里安诺的机器人学建模规划与控制一书中有这样的描述：代表的是广义坐标对应的广义力，它的每个分量由非保守力给出。而重力属于保守力（实际上这是我们在机器人动力学中唯一接触到的保守力，其他的如电场力等用不到），所以在广义力中剔除了重力项。而摩擦力、支持力、推力都是非保守力。

 

 我们可以发现最终又回到了牛顿第二定律，所以拉格朗日方程和牛顿第二定律是等价的，只是在形式上会有所不同。

三、单刚体动力学：

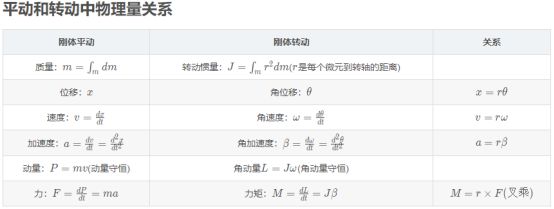
相对于质点而言，刚体的复杂性在于它本身质量的分布特性。即刚体本身是有形状的，而且它的质量并不是集中在一点上。因此，对于一个刚体我们除了要考虑它的平移运动还要考虑他的转动。

1、转动惯量：

物理意义：转动惯量是表征刚体转动惯性大小的物理量，衡量刚体抵抗旋转运动的惯性的物理量。它与刚体的质量以及质量相对于转轴的分布有关。

 

2、惯性矩：

 

3、惯性积：

 4、惯性张量：

在单自由度系统中，常常要考虑刚体的质量。对于定轴转动的情况，经常用到惯量矩这个概念。对一个可以在三维空间自由运动的刚体来说，可能存在无穷多个旋转轴。在一个刚体绕任意轴做旋转运动时，我们需要一种能够表征刚体质量分布的方法。这里需要引入惯性张量，它可以看做是对物体惯量的广义度量。

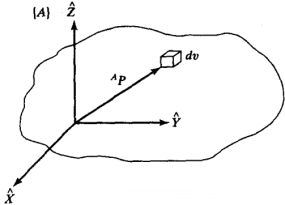
定义一组参量，给出刚体质量在参考坐标系中分布的信息。下图表示一个刚体，坐标系建立在刚体上。惯性张量可以在任何坐标系中定义，但一般在固连于刚体上的坐标系中定义惯性张量（为了简化惯性参数）。

 

矩阵中各元素为： 

 

 

转动惯量是描述刚体绕定轴转动惯性的量，而惯性张量则是描述刚体绕定点转动的惯性的量。

假设我们以刚体上的某一点建立了三维直角坐标系：

如果刚体只绕x轴旋转，并且我们只考虑刚体绕x轴的旋转运动惯性，那么我们只需要用一个量就能描述，这就是刚体围绕x轴的转动惯量，也就是惯性张量里面的这个量。如果刚体还是只绕x轴旋转，但是我们还需要考虑刚体绕x轴旋转时，对y轴和z轴的运动会产生什么影响，那么就需要另外两个量，也就是。 

再如果，刚体不仅仅绕x轴转动，还绕z和y轴旋转，那么就需要更多的量，一共就是9个量，所以就是惯性张量中的9个元素。

另外，转动惯量是惯性张量在对角线上的元素，也就是惯性矩；惯性积是惯性张量在非对角线上的元素。

 5、牛顿方程：

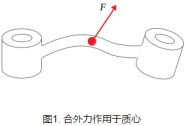
对于刚体而言牛顿第二定律依然能够用于描述刚体质心的运动。由于作用在刚体上的任意复杂力系都可以等价为作用于质心的合外力以及合外力矩。如下图1描述的是合外力F作用于刚体质心处。那么刚体线加速度和合外力之间的关系如下：。

 

6、欧拉方程：

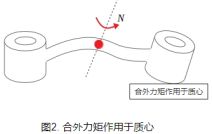
作用在刚体上的任意复杂力系最终都能等价为作用于质心的合外力以及合外力矩。合外力用于产生刚体质心加速度，合外力矩用于产生角加速度。如下图2描述的是合外力矩N作用于刚体质心处。根据欧拉方程给出的定义，刚体所受合外力矩与角加速度之间的关系如下（注意这个公式要求惯性系的原点必须与质心重合，原因将在欧拉方程的推导中介绍）：

即这个公式要求惯性系在刚体的质心上。如果惯性系不在刚体的质心上则欧拉公式为，其中​​​​​​​为质心在惯性系下的位置。

 

 

 要理解这个公式需要进行一些推导，过程比较繁琐，这里就不推导了，对于工程做到明白、理解和应用即可。

7、刚体动力学：

下面我们分析一个刚体的受力，并得到它的动力学方程，如下是连杆i的受力分析：

 下面先解释下图中各物理量的含义，且图中各物理量都是在连杆的质心坐标系下描述的：

 

 以上便是单刚体动力学方程。对于多连杆的串联机器人来说本质上也是逐个分析其中的每个连杆。但是对机器人来说如何求解各个连杆的速度、加速度、角速度、角加速度在其质心坐标系下的表达式才是基于牛顿欧拉法的机器人动力学真正难的地方。