位姿描述和坐标变换
引子
想象我们用手去拿起桌子上的杯子,我们会观察杯子所处的状态调整我们的手的状态。我们观察杯子状态是观察杯子的位姿,调整手状态也为调整手的位姿。位姿包括位置和姿态。调整手状态的过程即为坐标变换,将一个位姿转换为另一个位姿。那么位姿和坐标变换如何表达呢?

首先考虑刚体具有几个自由度?
1. 刚体描述
二维平面的刚体描述
如上图所示,对于二维平面的刚体,其可以沿着X轴和Y轴移动,可以绕着某个垂直平面的固定轴转动。因此二维平面刚体具有三个自由度:
- 两个自由度的移动
- 一个自由度的转动
三维空间的刚体描述
三维空间需要三个相互垂直的X、Y和Z坐标轴描述。三维平面的刚体可以沿着X轴、Y轴和Z轴移动,也可以绕着三维空间的X轴、Y轴和Z轴旋转。因此三维空间刚体具有六个自由度:
- 三个自由度的移动
- 三个自由度的转动
三维空间的刚体的三自由度移动和三自由度转动如何描述呢?如下图所示:
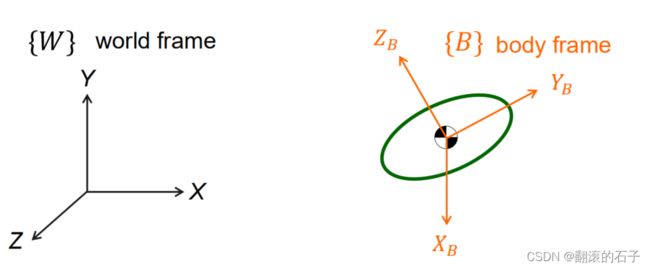
- 其移动可以使用坐标系原点位置判定
- 其转动可以使用坐标系姿态判定
使用什么描述刚体的位姿,即移动和转动呢?
2. 位姿描述
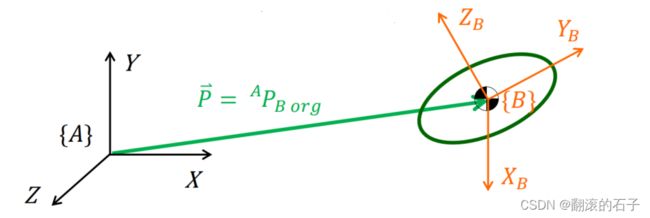
首先建立参考坐标系 { A } \{ A \} {A}和刚体坐标系 { B } \{ B \} {B}。
位置描述
刚体位置可以使用含有三个元素的位置矢量进行表示,如下图所示。
A P B O R G = [ P x P y P z ] ^{A}\textrm{P}_{BORG} = \begin{bmatrix} P_x\\ P_y\\ P_z \end{bmatrix} APBORG=⎣⎡PxPyPz⎦⎤
姿态描述
刚体姿态可以使用刚体坐标系 { B } \{ B \} {B}相对于参考坐标系 { A } \{ A \} {A}的主轴矢量 A X ^ B ^{A}\hat{X}_{B} AX^B、 A Y ^ B ^{A}\hat{Y}_{B} AY^B和 A Z ^ B ^{A}\hat{Z}_{B} AZ^B进行表示。通过将刚体坐标系 { B } \{ B \} {B}的主轴矢量 X ^ B \hat{X}_{B} X^B、 Y ^ B \hat{Y}_{B} Y^B和 Z ^ B \hat{Z}_{B} Z^B投影到参考坐标系 { A } \{ A \} {A}的主轴向量 X ^ A \hat{X}_{A} X^A、 Y ^ A \hat{Y}_{A} Y^A和 Z ^ A \hat{Z}_{A} Z^A得到。因此刚体姿态可以使用旋转矩阵表示:
B A R = ( A X ^ B , A Y ^ B , A Z ^ B ) = [ X ^ B ⋅ X ^ A Y ^ B ⋅ X ^ A Z ^ B ⋅ X ^ A X ^ B ⋅ Y ^ A Y ^ B ⋅ Y ^ A Z ^ B ⋅ Y ^ A X ^ B ⋅ Z ^ A Y ^ B ⋅ Z ^ A Z ^ B ⋅ Z ^ A ] _{B}^{A}\textrm{R} = (^{A}\hat{X}_{B}, ^{A}\hat{Y}_{B}, ^{A}\hat{Z}_{B})= \begin{bmatrix} \hat{X}_{B} \cdot \hat{X}_{A} & \hat{Y}_{B} \cdot \hat{X}_{A} & \hat{Z}_{B} \cdot \hat{X}_{A} \\ \hat{X}_{B} \cdot \hat{Y}_{A} & \hat{Y}_{B} \cdot \hat{Y}_{A} & \hat{Z}_{B} \cdot \hat{Y}_{A} \\ \hat{X}_{B} \cdot \hat{Z}_{A} & \hat{Y}_{B} \cdot \hat{Z}_{A} & \hat{Z}_{B} \cdot \hat{Z}_{A} \end{bmatrix} BAR=(AX^B,AY^B,AZ^B)=⎣⎡X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Z^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅Z^A⎦⎤
进一步观察,参考坐标系 { A } \{ A \} {A}相对于刚体坐标系 { B } \{ B \} {B}的姿态表示为:
A B R = [ B X ^ A B Y ^ A B Z ^ A ] = [ X ^ A ⋅ X ^ B X ^ A ⋅ Y ^ B X ^ A ⋅ Z ^ B Y ^ A ⋅ X ^ B Y ^ A ⋅ Y ^ B Y ^ A ⋅ Z ^ B Z ^ A ⋅ X ^ B Z ^ A ⋅ Y ^ B Z ^ A ⋅ Z ^ B ] A B R = B A R T _{A}^{B}\textrm{R} = \begin{bmatrix} ^{B}\hat{X}_{A}\\ ^{B}\hat{Y}_{A}\\ ^{B}\hat{Z}_{A} \end{bmatrix} = \begin{bmatrix} \hat{X}_{A} \cdot \hat{X}_{B} & \hat{X}_{A} \cdot \hat{Y}_{B} & \hat{X}_{A} \cdot \hat{Z}_{B} \\ \hat{Y}_{A} \cdot \hat{X}_{B} & \hat{Y}_{A} \cdot \hat{Y}_{B} & \hat{Y}_{A} \cdot \hat{Z}_{B} \\ \hat{Z}_{A} \cdot \hat{X}_{B} & \hat{Z}_{A} \cdot \hat{Y}_{B} & \hat{Z}_{A} \cdot \hat{Z}_{B} \end{bmatrix} \\ _{A}^{B}\textrm{R} = _{B}^{A}\textrm{R}^{T} ABR=⎣⎡BX^ABY^ABZ^A⎦⎤=⎣⎡X^A⋅X^BY^A⋅X^BZ^A⋅X^BX^A⋅Y^BY^A⋅Y^BZ^A⋅Y^BX^A⋅Z^BY^A⋅Z^BZ^A⋅Z^B⎦⎤ABR=BART
位姿描述
刚体坐标系 { B } \{ B \} {B}的位姿表示为:
{ B } = { B A R , A P B O R G } \{B\}=\{ _{B}^{A}\textrm{R}, ^{A}\textrm{P}_{BORG} \} {B}={BAR,APBORG}
如何描述坐标系 { B } \{ B \} {B}相对于坐标系 { A } \{ A \} {A}的关系呢?
3. 坐标变换
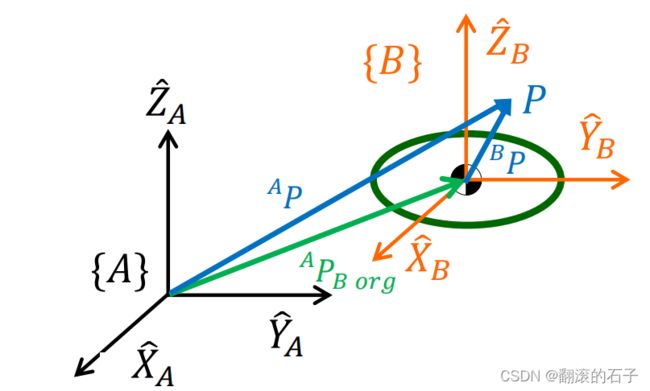
位置矢量和旋转矩阵不但可以描述刚体位姿,还可以用来表示对矢量或者点进行移动变换和旋转变换:
A P = B A R B P + A P B O R G [ A P 1 ] = [ B A R A P B O R G 0 1 ] ⋅ [ B P 1 ] ^{A}\textrm{P}=_{B}^{A}\textrm{R}^{B}\textrm{P}+^{A}\textrm{P}_{BORG} \\ \begin{bmatrix} ^{A}\textrm{P}\\ 1 \end{bmatrix}=\begin{bmatrix} _{B}^{A}\textrm{R} & ^{A}\textrm{P}_{BORG} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} ^{B}\textrm{P}\\ 1 \end{bmatrix} AP=BARBP+APBORG[AP1]=[BAR0APBORG1]⋅[BP1]
可以进一步定义变换矩阵:
B A T = [ B A R A P B O R G 0 1 ] A P = B A T B P _{B}^{A}\textrm{T}=\begin{bmatrix} _{B}^{A}\textrm{R} & ^{A}\textrm{P}_{BORG} \\ 0 & 1 \end{bmatrix} \\ ^{A}\textrm{P}=_{B}^{A}\textrm{T}^{B}\textrm{P} BAT=[BAR0APBORG1]AP=BATBP
位姿(坐标变换)具有六个自由度,坐标变换矩阵 T T T具有四个基础矩阵:
- 1个位移矩阵:
T r a n s ( p x , p y , p z ) = [ 1 0 0 p x 0 1 0 p y 0 0 1 p z 0 0 0 1 ] Trans(p_x, p_y, p_z) = \begin{bmatrix} 1 & 0 & 0 & p_x\\ 0 & 1 & 0 & p_y\\ 0 & 0 & 1 & p_z\\ 0 & 0 & 0 & 1 \end{bmatrix} Trans(px,py,pz)=⎣⎢⎢⎡100001000010pxpypz1⎦⎥⎥⎤
- 三个旋转矩阵扩展为变换矩阵:
R o t ( x , α ) = [ 1 0 0 0 0 c o s ( α ) s i n ( α ) 0 0 − s i n ( α ) c o s ( α ) 0 0 0 0 1 ] R o t ( y , α ) = [ c o s ( α ) 0 − s i n ( α ) 0 0 1 0 0 s i n ( α ) 0 c o s ( α ) 0 0 0 0 1 ] R o t ( z , α ) = [ c o s ( α ) s i n ( α ) 0 0 − s i n ( α ) c o s ( α ) 0 0 0 0 0 0 0 0 0 1 ] Rot(x,\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & cos(\alpha) & sin(\alpha) & 0\\ 0 & -sin(\alpha) & cos(\alpha) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \\ Rot(y,\alpha) = \begin{bmatrix} cos(\alpha) & 0 & -sin(\alpha) & 0\\ 0 & 1 & 0 & 0\\ sin(\alpha) & 0 & cos(\alpha) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \\ Rot(z,\alpha) = \begin{bmatrix} cos(\alpha) & sin(\alpha) & 0 & 0\\ -sin(\alpha) & cos(\alpha) & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} Rot(x,α)=⎣⎢⎢⎡10000cos(α)−sin(α)00sin(α)cos(α)00001⎦⎥⎥⎤Rot(y,α)=⎣⎢⎢⎡cos(α)0sin(α)00100−sin(α)0cos(α)00001⎦⎥⎥⎤Rot(z,α)=⎣⎢⎢⎡cos(α)−sin(α)00sin(α)cos(α)0000000001⎦⎥⎥⎤
坐标系 { B } \{ B \} {B}与坐标系 { A } \{ A \} {A}的相对关系如何转换?
4. 逆变换
已知坐标系 { B } \{ B \} {B}相对于坐标系 { A } \{ A \} {A},即 B A T _{B}^{A}\textrm{T} BAT已知,计算坐标系 { A } \{ A \} {A}相对于坐标系 { B } \{ B \} {B}的变换矩阵 A B T _{A}^{B}\textrm{T} ABT。
旋转矩阵为:
A B R = B A R T _{A}^{B}\textrm{R} = _{B}^{A}\textrm{R}^{T} ABR=BART
将 A P B O R G ^{A}\textrm{P}_{BORG} APBORG转换为坐标系 { B } \{ B \} {B}的描述为:
B ( A P B O R G ) = A B R A P B O R G + B P A O R G ^{B}(^{A}\textrm{P}_{BORG})=_{A}^{B}\textrm{R}^{A}\textrm{P}_{BORG}+^{B}\textrm{P}_{AORG} B(APBORG)=ABRAPBORG+BPAORG
公式左边为0,可得:
B P A O R G = − A B R A P B O R G = − B A R T A P B O R G ^{B}\textrm{P}_{AORG} = -_{A}^{B}\textrm{R}^{A}\textrm{P}_{BORG}=-_{B}^{A}\textrm{R}^{T}{^{A}\textrm{P}_{BORG}} BPAORG=−ABRAPBORG=−BARTAPBORG
坐标系 { A } \{ A \} {A}相对于坐标系 { B } \{ B \} {B}的变换矩阵 A B T _{A}^{B}\textrm{T} ABT为:
A B T = [ B A R T − B A R T A P B O R G 0 1 ] A B T = B A T − 1 _{A}^{B}\textrm{T}=\begin{bmatrix} _{B}^{A}\textrm{R}^{T} & -_{B}^{A}\textrm{R}^{T}{^{A}\textrm{P}_{BORG}} \\ 0 & 1 \end{bmatrix} \\ _{A}^{B}\textrm{T} = _{B}^{A}\textrm{T}^{-1} ABT=[BART0−BARTAPBORG1]ABT=BAT−1
参考
台大林沛群机器人:https://www.bilibili.com/video/BV1v4411H7ez?spm_id_from=333.851.header_right.fav_list.click