矩阵求导常用公式
矩阵求导常用公式
- 1 引言
- 2 向量的导数
-
- 2.1 向量对标量求导 Vector-by-scalar
- 2.2 标量对向量求导 Scalar-by-vector
- 2.3 向量对向量求导 Vector-by-vector
- 3 矩阵的导数
-
- 3.1 矩阵对标量求导 Matrix-by-scalar
- 3.2 标量对矩阵求导 Scalar-by-matrix
- 4 常用求导公式
-
- 4.1 向量对向量求导
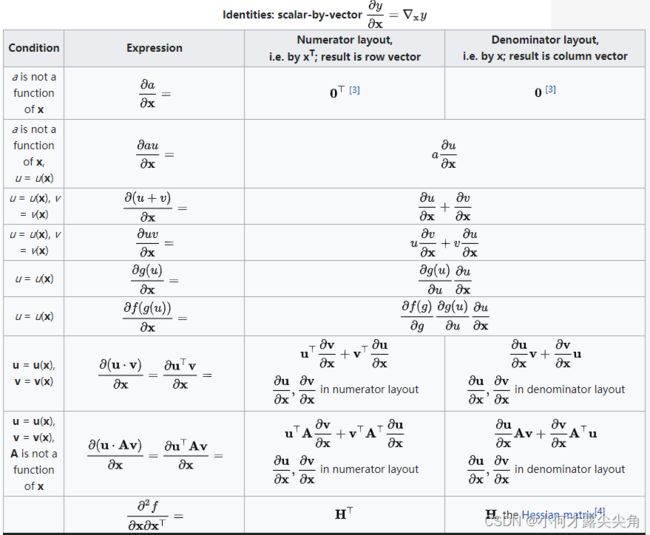
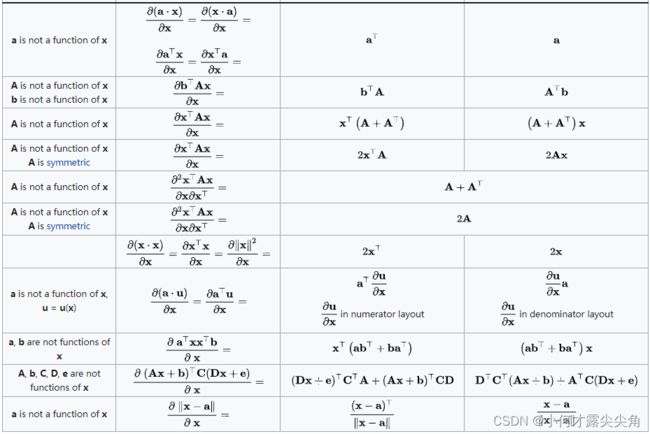
- 4.2 标量对向量求导
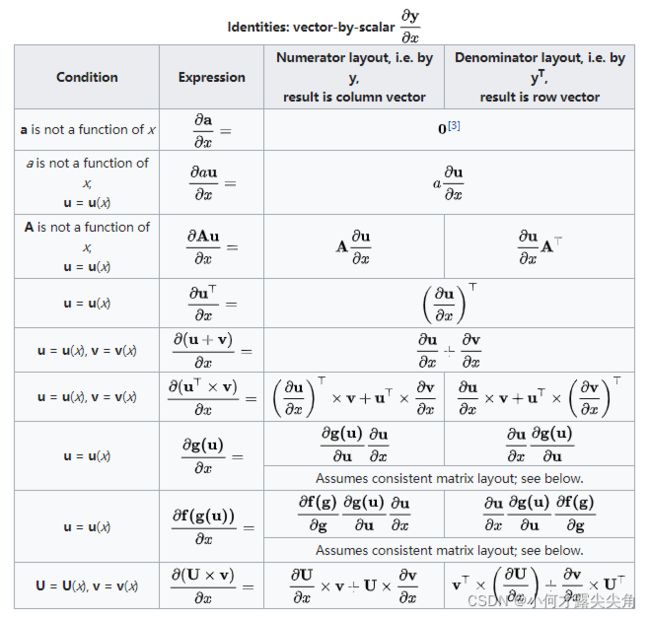
- 4.3 向量对标量求导
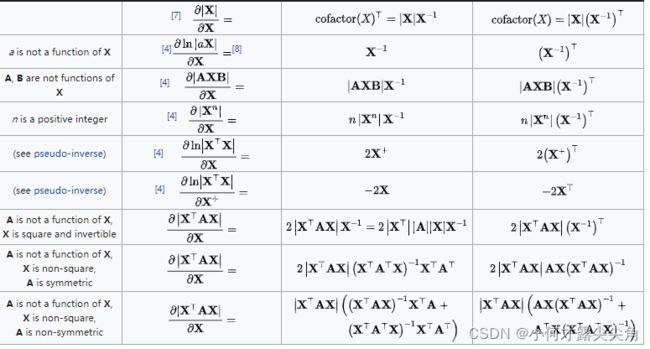
- 4.4 标量对矩阵求导
- 4.5 矩阵对标量求导
- 4.6 标量对标量求导
- 参考
1 引言
常见的求导有,标量对标量求导,向量对标量,矩阵对标量,标量对向量,向量对向量,标量对矩阵。求导的几种形式:

字符标示:
A 大写粗体表示矩阵
a 小写粗体表示向量
a 小写粗体表示标量
tr(X) 表示迹,主对角线之和
det(X) or |X| 表示
字母表前面部分表示常量(如 a,b,c…),字母表后面部分表示变量(如 t,x,y,…)
2 向量的导数
2.1 向量对标量求导 Vector-by-scalar
y 向量为 y = [ y 1 y 2 ⋯ y m ] T {\displaystyle \mathbf {y} ={\begin{bmatrix}y_{1}&y_{2}&\cdots &y_{m}\end{bmatrix}}^{\mathsf {T}}} y=[y1y2⋯ym]T, 对 x 求导,结果为列
∂ y ∂ x = [ ∂ y 1 ∂ x ∂ y 2 ∂ x ⋮ ∂ y m ∂ x ] {\displaystyle {\frac {\partial \mathbf {y} }{\partial x}}={\begin{bmatrix}{\frac {\partial y_{1}}{\partial x}}\\{\frac {\partial y_{2}}{\partial x}}\\\vdots \\{\frac {\partial y_{m}}{\partial x}}\\\end{bmatrix}}} ∂x∂y=⎣⎢⎢⎢⎡∂x∂y1∂x∂y2⋮∂x∂ym⎦⎥⎥⎥⎤
2.2 标量对向量求导 Scalar-by-vector
y 为标量,对向量 x = [ x 1 x 2 ⋯ x n ] T {\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}^{\mathsf {T}}} x=[x1x2⋯xn]T 求导,结果为行

2.3 向量对向量求导 Vector-by-vector
输出向量为 y = [ y 1 y 2 ⋯ y m ] T {\displaystyle \mathbf {y} ={\begin{bmatrix}y_{1}&y_{2}&\cdots &y_{m}\end{bmatrix}}^{\mathsf {T}}} y=[y1y2⋯ym]T,
输入向量为 x = [ x 1 x 2 ⋯ x n ] T {\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}^{\mathsf {T}}} x=[x1x2⋯xn]T
神经网络中全连接层的形式就是如此

这种矩阵也称为雅各布矩阵
3 矩阵的导数
3.1 矩阵对标量求导 Matrix-by-scalar
3.2 标量对矩阵求导 Scalar-by-matrix
4 常用求导公式
字符标示:
a, b, c, d, and e 为常量, 标量 u, and v 由 x, x, or X中的一个计算而来;
a, b, c, d, and e 为常量向量, 向量 u, and v 由 x, x, or X中的一个计算而来;
A, B, B, D, and E 为常量矩阵, 向量 U, and V 由 x, x, or X中的一个计算而来;
4.1 向量对向量求导
4.2 标量对向量求导
4.3 向量对标量求导
4.4 标量对矩阵求导
4.5 矩阵对标量求导
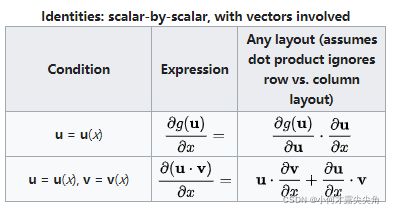
4.6 标量对标量求导
参考
Matrix calculus