实验三、图像复原

1.  实验目的

(1) 理解退化模型。

(2) 掌握常用的图像复原方法。

2.  实验内容

(1) 模拟噪声的行为和影响的能力是图像复原的核心。 示例 1 ：使用 imnoise 添加噪声。

J = imnoise(I,'gaussian')  将方差为 0.01  的零均值高斯白噪声添加到灰度图像 I。 J = imnoise(I,'gaussian',m)  添加高斯白噪声，均值为 m ，方差为 0.01。

J = imnoise(I,'gaussian',m,var_gauss)  添加高斯白噪声，均值为 m ，方差为 var_gauss。 J = imnoise(I,'localvar',var_local)  添加局部方差为 var_local  的零均值高斯白噪声。

J = imnoise(I,'localvar',intensity_map,var_local)  添加零均值高斯白噪声。噪声的局部方差 var_local 是 I 中图像强度值的函数。图像强度值到噪声方差的映射由向量 intensity_map 指定。

J = imnoise(I,'poisson')  从数据中生成泊松噪声，而不是向数据中添加人为噪声。有关详 细信息，请参阅算法。

J = imnoise(I,'salt & pepper')  添加椒盐噪声，默认噪声密度为 0.05。这会影响大约 5%  的 像素。示例 J = imnoise(I,'salt & pepper',d)  添加椒盐噪声，其中 d 是噪声密度。这会影响 大约 d*numel(I)  个像素。

J = imnoise(I,'speckle')使用方程 J = I+n*I  添加乘性噪声，其中 n 是均值为 0、方差为 0.05 的均匀分布随机噪声。

J = imnoise(I,'speckle',var_speckle)  添加方差为 var_speckle  的乘性噪声。

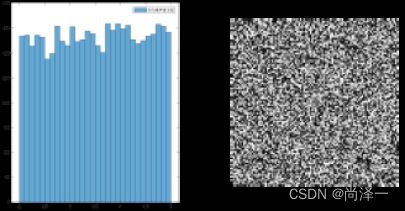
示例 2 ：使用指定的分布产生空间随机噪声。

均匀噪声实例z = a + (b 一 a) xU(0, 1)

 

clear

clc

a=2;

b=5;

noise= a + (b - a) * rand(100, 100) ;

blackIm=zeros( 100, 100);

noisedIm=noise + blackIm;

subplot(1,2, 1);histogram(noisedIm);

subplot(1,2,2);imshow(noisedIm,[])

示例 3 ：自编程实现指定噪声与周期噪声 (见资料 imnoise2.m, imnoise3.m  文件)

例：利用椒盐噪声污染图像

[M,N]=size(f);

R=imnoise2('salt & pepper',M,N,0. 1,0);

gp=f;

gp(R==0)=0;

subplot(1,2, 1),imshow(f);

subplot(1,2,2),imshow(gp);

%图像是被概率只有 0. 1 的胡椒噪声污染的 uint8 类图像，图像上出现大量黑点 (胡椒状)。

[M,N]=size(f);

R=imnoise2('salt & pepper',M,N,0,0. 1);

gp=f;

gp(R==1)=255;

figure

subplot(121),imshow(f);

subplot(122),imshow(gp);

%图像是被概率只有 0. 1 的盐粒噪声污染的 uint8 类图像，图像上出现大量白点 (盐粒状)。

注意，由椒盐噪声生成的噪声数组有三个值：对应于胡椒噪声的 0 ，对应于盐粒噪 声的 1 ，以及对应于无噪声的 0.5。为了使这个数组有用，还需要对他进—步的处理。椒 盐噪声污染图像时，需要找到 R 中所有的 0 值坐标，把相应原图像的坐标位置置为最小 灰度值，找到 R 中值为 1 的坐标，把相应原图像的坐标位置置为最大灰度值。

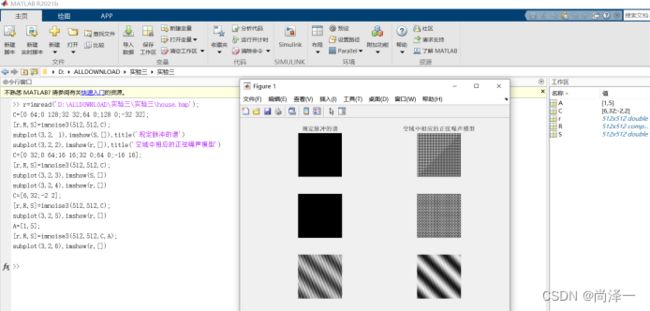
例：利用周期噪声污染图像

 

C=[0 64;0 128;32 32;64 0;128 0;-32 32];

[r,R,S]=imnoise3(512,512,C);

subplot(3,2, 1),imshow(S,[]),title('规定脉冲的谱')

subplot(3,2,2),imshow(r,[]),title('空域中相应的正弦噪声模型')

C=[0 32;0 64;16 16;32 0;64 0;-16 16];

[r,R,S]=imnoise3(512,512,C);

subplot(3,2,3),imshow(S,[])

subplot(3,2,4),imshow(r,[])

C=[6,32;-2 2];

[r,R,S]=imnoise3(512,512,C);

subplot(3,2,5),imshow(r,[])

A=[1,5];

[r,R,S]=imnoise3(512,512,C,A);

subplot(3,2,6),imshow(r,[])

注意：图像出现周期噪声通常源于电气，电机的干扰，通常通过在频域滤波来处理。

周期噪声的噪声模型是—个离散的二维正弦波，方程为：

r (x, y ) = Asin 【2xp0 (x + Bx )/ M + 2xv0 (y + By ) / N】 

其中，x=0, 1,2 ，… ，M-1 且 y=0, 1,2, … ,N- 1 ；A 是振幅，u0 和 v0 分别确定了关于 x 轴和 y 轴的正弦频率。Bx 和 By 分别是关于原点的相移。定义—个 M 函数接受任意数量的脉 冲位置 (频率坐标)，每个脉冲位置都有自己的振幅，频率和相移参数。该函数还能够

输出各个正弦波之和的傅里叶变换以及谱。

C 是具有 K 对频率的 K×2 矩阵。定义频率中脉冲位置的域坐标(u, v) 。这些位置相对于 频率矩形中心在(floor(M/2) + 1, floor(N/2) + 1) 。脉冲位置被指定为相对于中心的增量。 例如，如果 M = N = 512 ，则中心位于 (257, 257) 。要指定 (280, 300)  处的脉冲，我们 指定对 (23, 43)；即 257 + 23 = 280 和 257 + 43 = 300 。每个脉冲只需要一对坐标。

(2) 空域滤波

help imfilter

imfilter -  多维图像的 N  维滤波

此 MATLAB  函数 使用多维滤波器 h  对多维数组 A 进行滤波，并在 B  中返回 结果。

B = imfilter(A,h)

B = imfilter(A,h,options,...)

h = fspecial(type)

type -  滤波器的类型

'average' | 'disk' | 'gaussian' | 'laplacian' | 'log' | 'motion' | 'prewitt' | 'sobel'

help medfilt2

medfilt2 -  二维中位数滤波

此 MATLAB  函数 对图像 I  执行二维中位数滤波。每个输出像素包含输入图像中 对应像素周围 3×3  邻域的中位数值。

J = medfilt2(I)

J = medfilt2(I,[m n])

J = medfilt2(___,padopt)

实验一

1. 1 产生至少 2 种不同类型的噪声，并绘制原图像、加噪后图像及对应直方图于 一个图形窗口中[subplot(m,n,p)]。

1.2 对有椒盐噪声图像进行 5×5 方形窗口中值滤波。

附加内容： 自编程实现均值、中值、 自适应中值滤波器

(2) — 幅退化的图像可以近似地用方程 g=Hf+n 表示 ，其中 g 为图像，H 为变形算子 ，又称为点扩散函数 (PSF)，f 为原始的真实图像，n 为附加噪声， 它在图像捕获过程中产生并且使图像质量变坏。其中，PSF 是—个很重要的因素， 它的值直接影响到恢复后图像的质量。

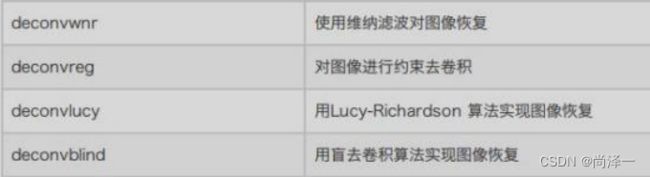
MATLAB工具箱中有 4 个图像恢复函数。这 4 个函数都以—个 PSF 和模糊 图像作为主要变量。deconvwnr 函数使用维纳滤波对图像恢复，求取最小二乘解， deconvreg 函数实现约束去卷积，求取有约束的最小二乘解，可以设置对输出图 像的约束。deconvlucy 函数实现了—个加速衰减的 Lucy-Richardson 算法。该函 数采用优化技术和泊松统计量进行多次迭代。使用该函数，不需要提供有关模糊 图像中附加噪声的信息。deconvblind 函数使用的是盲去卷积算法，它在不知道 PSF 的情况下进行恢复。调用deconvblind 函数时，将 PSF 的初值作为—个变量 进行传递。该函数除了返回—个修复后的图像以外，还返回—个修复后的 PSF。

 

示例：使用维纳滤波恢复图像

J=deconvwnr(I,psf,nsr)使用 Wiener 滤波算法对图像 I 进行反卷积，从而返回去模糊后的 图像 J 。psf 是 I 进行卷积的点扩散函数(PSF) 。nsr 是加性噪声的噪信功率比。在估计图 像与真实图像之间的最小均方误差意义上，该算法是最优的。

J = deconvwnr(I,psf,ncorr,icorr)对图像I 进行反卷积，其中ncorr 是噪声的自相关函数，icorr 是原始图像的自相关函数。

J = deconvwnr(I,psf)使用 Wiener 滤波算法对图像 I 进行反卷积，无估计噪声。在不含噪 情况下，Wiener 滤波等效于理想的逆滤波。

%读取图片到工作区

I = im2double(imread('cameraman.tif'));

imshow(I);

title('Original Image (courtesy of MIT)');

%模拟一个运动模糊

LEN = 21;

THETA = 11;

PSF = fspecial('motion', LEN, THETA);

blurred = imfilter(I, PSF, 'conv', 'circular');

figure, imshow(blurred)

%模拟加性噪声

noise_mean = 0;

noise_var = 0.0001;

blurred_noisy = imnoise(blurred, 'gaussian', noise_mean, noise_var);

figure, imshow(blurred_noisy)

title('Simulate Blur and Noise')

%假定噪声为 0 ，恢复图像

estimated_nsr = 0;

wnr2 = deconvwnr(blurred_noisy, PSF, estimated_nsr);

figure, imshow(wnr2)

title('Restoration of Blurred, Noisy Image Using NSR = 0')

%使用最佳噪声/信号功率比恢复图像

estimated_nsr = noise_var / var(I(:));

wnr3 = deconvwnr(blurred_noisy, PSF, estimated_nsr);

figure, imshow(wnr3)

title('Restoration of Blurred, Noisy Image Using Estimated NSR');

实验二（选做其一）

2. 1  选择一幅清晰的灰度图像，对该图像进行模糊化处理，然后分别采用逆滤波、 维纳滤波和约束最小二乘方滤波对模糊图像进行复原，比较各种图像复原方法的 复原效果。

2.2  选择一幅清晰的灰度图像，对该图像进行模糊化处理并加入不同强度的高斯 噪声，然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对退化图像进行复 原，比较各种图像复原方法的复原效果。

附加内容： 自编程实现不同截至频率的逆滤波并比较其复原效果。

Matlab help 图像去模糊_长笛人倚楼Gloria_新浪博客 (sina.com.cn)