BZOJ 1927 星际竞速(最小费用最大流)
题目链接:http://61.187.179.132/JudgeOnline/problem.php?id=1927
题意:一个图,n个点。对于给出的每条边 u,v,w,表示u和v中编号小的那个到编号大的那个的时间为w。另外有n个值Ai,表示从任何一个点到达i点的时间为Ai。初始时你在n个点之外的一个 点上,我们称其为初始点B。要求从B出发,遍历n个点每个点一次,求最小时间。显然开始你只能使用Ai从B到达n个点中的某个点,因为B到n个点中没有其 他的边。
思路:因为最后停在了某个点上,那么从B出 发其实一共走过了n条边,n个点中每个点都有一个1的入度,n个点中有n-1个点有一个1的出度。那么,我们将n个点拆成两个点,出度点和入读点,源点S 向每个出度点连边<1,0>(流量1,费用0),每个入度点向汇点T连边<1,0>。S向每个入度点连 边<1,Ai>,每个出度点向入度点连边<1,w>(这两个点有边的话,且只能从小的向大的连),那么样例中的数据得到的图为:
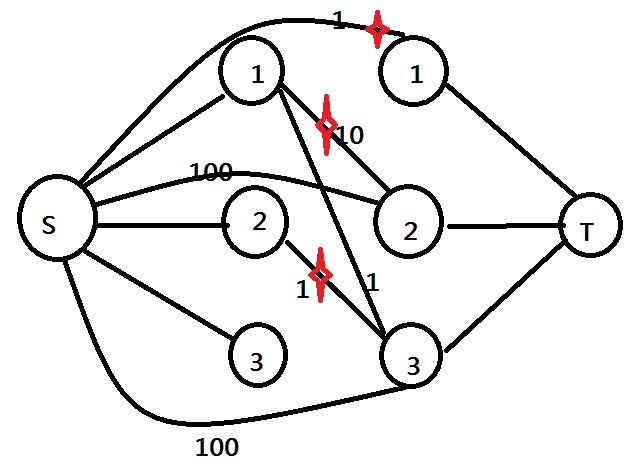
其中红色的为最后最小费用最大流中的边。因 为每个入度点到T的流为1,所以到达这个点的要么从S要么从出度点,且只有一条,保证了一共有n条边,从S出发的至少有一条,就等价于从B出发的一条,那 么若还有其他从S出发的,那么必然存在有些出度点没有到入度点的边,那么从S出发的可以看做从这个出度点经过Ai到达相应的入度点。
struct node
{
int u,v,flow,cost,next;
};
node edges[N*100];
int head[N],e;
void add(int u,int v,int flow,int cost)
{
edges[e].u=u;
edges[e].v=v;
edges[e].cost=cost;
edges[e].flow=flow;
edges[e].next=head[u];
head[u]=e++;
}
void Add(int u,int v,int flow,int cost)
{
add(u,v,flow,cost);
add(v,u,0,-cost);
}
int C[N],F[N],pre[N],s,t;
int visit[N];
int SPFA(int s,int t)
{
clr(pre,-1);
queue<int> Q;
Q.push(s);
int i;
FOR0(i,t+1) C[i]=INF,F[i]=0,visit[i]=0;
int u,v,c,f;
C[s]=0; F[s]=INF;
while(!Q.empty())
{
u=Q.front();
Q.pop();
visit[u]=0;
for(i=head[u];i!=-1;i=edges[i].next)
{
v=edges[i].v;
c=edges[i].cost;
f=edges[i].flow;
if(f>0&&C[v]>C[u]+c)
{
C[v]=C[u]+c;
F[v]=min(F[u],f);
pre[v]=i;
if(!visit[v])
{
Q.push(v);
visit[v]=1;
}
}
}
}
return F[t];
}
int MCMF(int s,int t)
{
int ans=0,i,temp,x;
while(temp=SPFA(s,t))
{
for(i=t;i!=s;i=edges[pre[i]].u)
{
x=pre[i];
ans+=temp*edges[x].cost;
edges[x].flow-=temp;
edges[x^1].flow+=temp;
}
}
return ans;
}
int n,m;
int main()
{
RD(n,m); s=0; t=n+n+1; clr(head,-1); e=0;
int i,x,y,z;
FOR1(i,n) RD(x),Add(s,n+i,1,x);
FOR1(i,m)
{
RD(x,y,z);
if(x>y) swap(x,y);
Add(x,n+y,1,z);
}
FOR1(i,n)
{
Add(s,i,1,0);
Add(n+i,t,1,0);
}
PR(MCMF(s,t));
}