最短路径—Dijkstra算法和Floyd算法
Dijkstra算法
1、概述
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法。
注意该算法要求图中不存在负权边。
问题描述:
在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
2、算法描述
2.1 算法思想:
(1)设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组;
(2)第一组为已求出最短路径的顶点集合(用S表示),初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法结束;
(3)第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2.2 算法步骤:
(1)初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则
(2)从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
(4)重复步骤b和c直到所有顶点都包含在S中。
3、演示
给出一个无向图

用Dijkstra算法找出以A为起点的单源最短路径步骤如下:

4、算法实现(python)
"""
Dijkstra 算法:
计算指定点 v0 到图 G 中任意点的最短路径的距离
基本思想:
(1) 每次找到离源点最近的一个顶点,然后以该顶点为中间点进行扩展;
(2) 最终得到源点到其余所有点的最短路径;
(3) 该算法是一种贪婪算法
其中:
INF 为设定的无限远距离值
此方法不能解决负权值边的图
"""
def Dijkstra(G, v0, INF=999):
# S为已求出最短路径的顶点集合
S = set()
minv = v0
# 源顶点到其余各顶点的初始路程
dis = dict((k, INF) for k in G.keys())
dis[v0] = 0
while len(S) < len(G):
# minv设为中间点
S.add(minv)
# 从中间点minv开始向后找:找到最短距离并更新距离字典
for w in G[minv]:
# 如果dis(开始,中间点) + (中间点,连接点) < 已知最短距离
if dis[minv] + G[minv][w] < dis[w]:
# 对已知最短距离进行更新
dis[w] = dis[minv] + G[minv][w]
# 从剩下的未确定顶点集合U中选择最小距离点作为新的扩散点
new_node = INF
for v in dis.keys():
# 跳过已确定最短距离的点
if v in S: continue
if dis[v] < new_node:
new_node = dis[v]
# 求最小距离点,作为新的扩散点
minv = v
return dis
if __name__ == '__main__':
G = {1:{1:0, 2:1, 3:12},
2:{2:0, 3:9, 4:3},
3:{3:0, 5:5},
4:{3:4, 4:0, 5:13, 6:15},
5:{5:0, 6:4},
6:{6:0}}
dis = Dijkstra(G,v0=1)
for item in dis:
print("从1点到", item, "点最短距离为:", dis[item])
运行结果:
从1点到 1 点最短距离为: 0
从1点到 2 点最短距离为: 1
从1点到 3 点最短距离为: 8
从1点到 4 点最短距离为: 4
从1点到 5 点最短距离为: 13
从1点到 6 点最短距离为: 17
Floyd算法
1、算法特点:
弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。 Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
2、算法思想:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
3、算法过程:
通过Floyd计算图G=(V,E)中各个顶点的最短路径时,需要引入两个矩阵,矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j]记录路径,表示顶点i到顶点j经过了b[i][j]记录的顶点。
(1)假设图G中顶点个数为N,则需要对矩阵D和矩阵P进行N次更新;
(2)初始时,矩阵D中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞,矩阵P的值为顶点b[i][j]的j的值。
(3)接下来开始对矩阵D进行N次更新。第1次更新时,如果”a[i][j]的距离” > “a[i][0]+a[0][j]”(a[i][0]+a[0][j]表示”i与j之间经过第1个顶点的距离”),则更新a[i][j]为”a[i][0]+a[0][j]”, 更新b[i][j]=b[i][0]。
(4)同理,第k次更新时,如果”a[i][j]的距离” > “a[i][k-1]+a[k-1][j]”,则更新a[i][j]为”a[i][k-1]+a[k-1][j]”,b[i][j]=b[i][k-1]。
(5)更新N次之后,操作完成!
4、图示:

第一步,我们先初始化两个矩阵,得到下图两个矩阵:


第二步,以v1为中介点,更新两个矩阵: 发现,a[1][0]+a[0][6] < a[1][6] 和a[6][0]+a[0][1] < a[6][1],所以我们只需要矩阵D和矩阵P,结果如下:
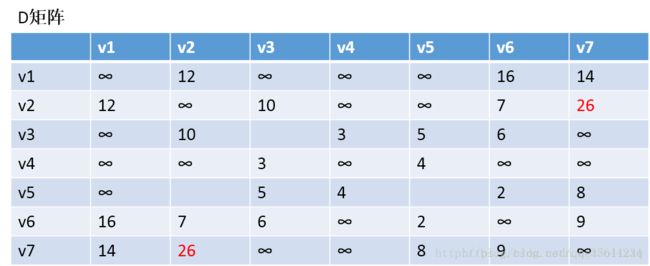
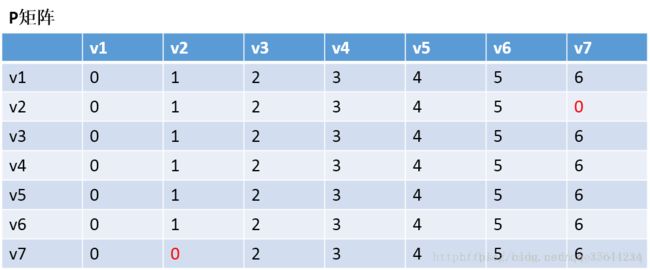
通过矩阵P,我发现v2–v7的最短路径是:v2–v1–v7 第三步:以v2作为中介点,来更新我们的两个矩阵,使用同样的原理,扫描整个矩阵,得到如下图的结果:
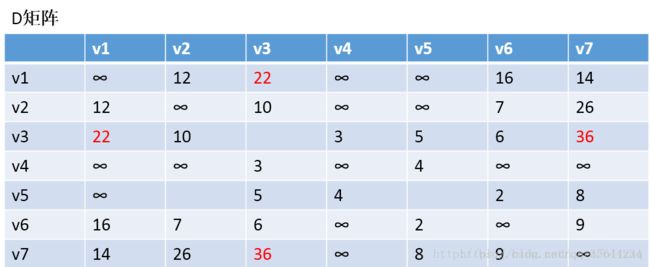

Floyd算法每次都会选择一个中介点k,然后,遍历整个矩阵,查找需要更新的值。
5、算法实现:
"""
Floyd算法:
"""
## 表示无穷大
INF_val = 9999
class Floyd_Path():
def __init__(self, node, node_map, path_map):
self.node = node
self.node_map = node_map
self.node_length = len(node_map)
self.path_map = path_map
self._init_Floyd()
def __call__(self, from_node, to_node):
self.from_node = from_node
self.to_node = to_node
return self._format_path()
def _init_Floyd(self):
for k in range(self.node_length):
for i in range(self.node_length):
for j in range(self.node_length):
tmp = self.node_map[i][k] + self.node_map[k][j]
if self.node_map[i][j] > tmp:
self.node_map[i][j] = tmp
self.path_map[i][j] = self.path_map[i][k]
print('_init_Floyd is end')
def _format_path(self):
node_list = []
temp_node = self.from_node
obj_node = self.to_node
print("the shortest path is:", self.node_map[temp_node][obj_node])
node_list.append(self.node[temp_node])
while True:
node_list.append(self.node[self.path_map[temp_node][obj_node]])
temp_node = self.path_map[temp_node][obj_node]
if temp_node == obj_node:
break
return node_list
def set_node_map(node_map, node, node_list, path_map):
for i in range(len(node)):
## 对角线为0
node_map[i][i] = 0
for x, y, val in node_list:
node_map[node.index(x)][node.index(y)] = node_map[node.index(y)][node.index(x)] = val
path_map[node.index(x)][node.index(y)] = node.index(y)
path_map[node.index(y)][node.index(x)] = node.index(x)
if __name__ == "__main__":
node = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 9), ('A', 'B', 10), ('A', 'G', 15), ('B', 'F', 2),
('G', 'F', 3), ('G', 'E', 12), ('G', 'C', 10), ('C', 'E', 1),
('E', 'D', 7)]
## node_map[i][j] 存储i到j的最短距离
node_map = [[INF_val for val in range(len(node))] for val in range(len(node))]
## path_map[i][j]=j 表示i到j的最短路径是经过顶点j
path_map = [[0 for val in range(len(node))] for val in range(len(node))]
## set node_map
set_node_map(node_map, node, node_list, path_map)
## select one node to obj node, e.g. A --> D(node[0] --> node[3])
from_node = node.index('A')
to_node = node.index('E')
Floydpath = Floyd_Path(node, node_map, path_map)
path = Floydpath(from_node, to_node)
print(path)
运行结果:
_init_Floyd is end
the shortest path is: 23
['A', 'F', 'G', 'C', 'E']
参考:
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
https://blog.csdn.net/qq_35644234/article/details/60875818
