金融风控-- ＞申请评分卡模型-- ＞特征工程（特征分箱，WOE编码）

这篇博文主要讲在申请评分卡模型中常用的一些特征工程方法，申请评分卡模型最多的还是logsitic模型。

先看数据，我们现在有三张表：

已加工成型的信息：

Master表
idx:每一笔贷款的unique key,可以与另外2个文件里的idx相匹配。
UserInfo_:借款人特征字段
WeblogInfo_:Info网络行为字段
Education_Info*:学历学籍字段
ThirdParty_Info_PeriodN_:第三方数据时间段N字段
SocialNetwork_:社交网络字段
ListingInfo:借款成交时间
Target:违约标签(1 = 贷款违约,0 = 正常还款)

需要衍生的信息

借款人的登陆信息表
ListingInfo:借款成交时间
LogInfo1:操作代码
LogInfo2:操作类别
LogInfo3:登陆时间
idx:每一笔贷款的unique key

客户在不同的时间段内有着不同的操作，故我们最好做个时间切片，在每个时间切片内统计一些特征。从而衍生出一些特征。

时间切片:

两个时刻间的跨度

例: 申请日期之前30天内的登录次数
申请日期之前第30天至第59天内的登录次数

基于时间切片的衍生

申请日期之前180天内,平均每月(30天)的登录次数

常用的时间切片

(1、2个)月,(1、2个)季度,半年,1年,1年半,2年

时间切片的选择

不能太长:保证大多数样本都能覆盖到
不能太短:丢失信息

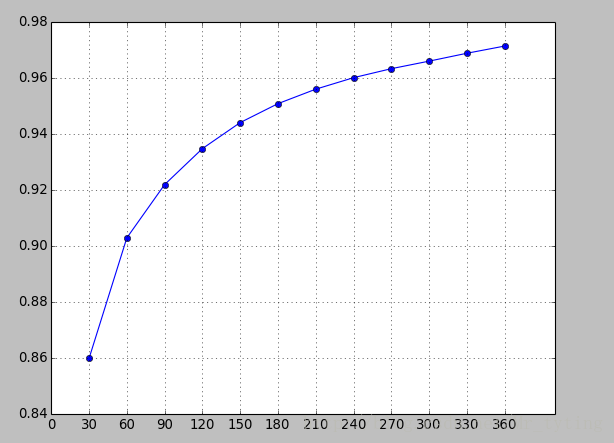
我们希望最大时间切片不能太长，都是最好又能包含大部分信息。那么最大切片应该多大呢？

#coding:utf-8
import pandas as pd
import datetime
import collections
import numpy as np
import random

import matplotlib.pyplot as plt

def TimeWindowSelection(df, daysCol, time_windows):
    '''
    :param df: the dataset containg variabel of days
    :param daysCol: the column of days
    :param time_windows: the list of time window，可分别取30,60,90,,,360
    :return:
    '''
    freq_tw = {}
    for tw in time_windows:
        freq = sum(df[daysCol].apply(lambda x: int(x<=tw))) ##统计在tw时间切片内客户操作的总次数
        freq_tw[tw] = freq/float(len(df))　##tw时间切片内客户总操作数占总的操作数比例
    return freq_tw


data1 = pd.read_csv('PPD_LogInfo_3_1_Training_Set.csv', header = 0)
### Extract the applying date of each applicant
data1['logInfo'] = data1['LogInfo3'].map(lambda x: datetime.datetime.strptime(x,'%Y-%m-%d'))
data1['Listinginfo'] = data1['Listinginfo1'].map(lambda x: datetime.datetime.strptime(x,'%Y-%m-%d'))
data1['ListingGap'] = data1[['logInfo','Listinginfo']].apply(lambda x: (x[1]-x[0]).days,axis = 1)
timeWindows = TimeWindowSelection(data1, 'ListingGap', range(30,361,30))
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.plot(list(timeWindows.keys()),list(timeWindows.values()),marker='o')
ax.set_xticks([0,30,60,90,120,150,180,210,240,270,300,330,360])
ax.grid()
plt.show()

由上图可以看出，在0-180天的时间切片内的操作数占总的操作数的95%，180天以后的覆盖度增长很慢。所以我们选择180天为最大的时间切片。凡是不超过180天的时间切片，都可以用来做个特征衍生。

选取[7,30,60,90,120,150,180]做为不同的切片,衍生变量。

那么我们来选择提取哪些有用的特征：

• 统计下LogInfo1和LogInfo2在每个时间切片内被操作的次数m1。
• 统计下LogInfo1和LogInfo2在每个时间切片内不同的操作次数m2。
• 统计下LogInfo1和LogInfo2在每个时间切片内m1/m2的值。

time_window = [7, 30, 60, 90, 120, 150, 180]
var_list = ['LogInfo1','LogInfo2']
data1GroupbyIdx = pd.DataFrame({'Idx':data1['Idx'].drop_duplicates()})
for tw in time_window:
    data1['TruncatedLogInfo'] = data1['Listinginfo'].map(lambda x: x + datetime.timedelta(-tw))
    temp = data1.loc[data1['logInfo'] >= data1['TruncatedLogInfo']]
    for var in var_list:
        #count the frequences of LogInfo1 and LogInfo2
        count_stats = temp.groupby(['Idx'])[var].count().to_dict()
        data1GroupbyIdx[str(var)+'_'+str(tw)+'_count'] = data1GroupbyIdx['Idx'].map(lambda x: count_stats.get(x,0))
        # count the distinct value of LogInfo1 and LogInfo2
        Idx_UserupdateInfo1 = temp[['Idx', var]].drop_duplicates()
        uniq_stats = Idx_UserupdateInfo1.groupby(['Idx'])[var].count().to_dict()
        data1GroupbyIdx[str(var) + '_' + str(tw) + '_unique'] = data1GroupbyIdx['Idx'].map(lambda x: uniq_stats.get(x,0))
        # calculate the average count of each value in LogInfo1 and LogInfo2
        data1GroupbyIdx[str(var) + '_' + str(tw) + '_avg_count'] = data1GroupbyIdx[[str(var)+'_'+str(tw)+'_count',str(var) + '_' + str(tw) + '_unique']].\
            apply(lambda x: x[0]*1.0/x[1], axis=1)
            

数据清洗

对于类别型变量

		删除缺失率超过50%的变量
		剩余变量中的缺失做为一种状态

对于连续型变量

		删除缺失率超过30%的变量
		利用随机抽样法对剩余变量中的缺失进行补缺

注:连续变量中的缺失也可以当成一种状态

特征分箱（连续变量离散化或类别型变量使其更少类别）
分箱的定义

• 将连续变量离散化
• 将多状态的离散变量合并成少状态

分箱的重要性及其优势

0. 离散特征的增加和减少都很容易，易于模型的快速迭代；
1. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
2. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
3. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
4. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
5. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
6. 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。
7. 可以将缺失作为独立的一类带入模型。
8. 将所有变量变换到相似的尺度上。

特征分箱的方法
　

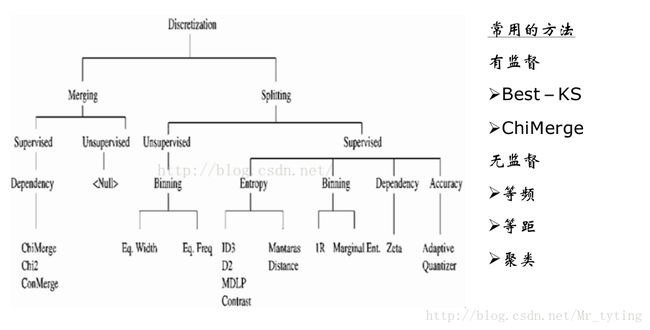
这里我们主要讲有监督的卡方分箱法(ChiMerge)。

自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
　　基本思想:对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。

分箱步骤：

这里需要注意初始化时需要对实例进行排序，在排序的基础上进行合并。

卡方阈值的确定：

根据显著性水平和自由度得到卡方值
　　自由度比类别数量小1。例如：有3类,自由度为2，则90%置信度(10%显著性水平)下，卡方的值为4.6。

阈值的意义

类别和属性独立时,有90%的可能性,计算得到的卡方值会小于4.6。
　　大于阈值4.6的卡方值就说明属性和类不是相互独立的，不能合并。如果阈值选的大,区间合并就会进行很多次,离散后的区间数量少、区间大。
　　
注:
1,ChiMerge算法推荐使用0.90、0.95、0.99置信度,最大区间数取10到15之间.
2,也可以不考虑卡方阈值,此时可以考虑最小区间数或者最大区间数。指定区间数量的上限和下限,最多几个区间,最少几个区间。
3,对于类别型变量,需要分箱时需要按照某种方式进行排序。

按照最大区间数进行分箱代码：

def Chi2(df, total_col, bad_col, overallRate):
    '''
    :param df: the dataset containing the total count and bad count
    :param total_col: total count of each value in the variable
    :param bad_col: bad count of each value in the variable
    :param overallRate: the overall bad rate of the training set
    :return: the chi-square value
    '''
    df2 = df.copy()
    df2['expected'] = df[total_col].apply(lambda x: x*overallRate)
    combined = zip(df2['expected'], df2[bad_col])
    chi = [(i[0]-i[1])**2/i[0] for i in combined]
    chi2 = sum(chi)
    return chi2


### ChiMerge_MaxInterval: split the continuous variable using Chi-square value by specifying the max number of intervals
def ChiMerge_MaxInterval_Original(df, col, target, max_interval = 5):
    '''
    :param df: the dataframe containing splitted column, and target column with 1-0
    :param col: splitted column
    :param target: target column with 1-0
    :param max_interval: the maximum number of intervals. If the raw column has attributes less than this parameter, the function will not work
    :return: the combined bins
    '''
    colLevels = set(df[col])
    # since we always combined the neighbours of intervals, we need to sort the attributes
    colLevels = sorted(list(colLevels))　## 先对这列数据进行排序，然后在计算分箱
    N_distinct = len(colLevels)
    if N_distinct <= max_interval:  #If the raw column has attributes less than this parameter, the function will not work
        print "The number of original levels for {} is less than or equal to max intervals".format(col)
        return colLevels[:-1]
    else:
        #Step 1: group the dataset by col and work out the total count & bad count in each level of the raw column
        total = df.groupby([col])[target].count()
        total = pd.DataFrame({'total':total})
        bad = df.groupby([col])[target].sum()
        bad = pd.DataFrame({'bad':bad})
        regroup =  total.merge(bad,left_index=True,right_index=True, how='left')##将左侧，右侧的索引用作其连接键。
        regroup.reset_index(level=0, inplace=True)
        N = sum(regroup['total'])
        B = sum(regroup['bad'])
        #the overall bad rate will be used in calculating expected bad count
        overallRate = B*1.0/N　##　统计坏样本率
        # initially, each single attribute forms a single interval
        groupIntervals = [[i] for i in colLevels]## 类似于[[1],[2],[3,4]]其中每个[.]为一箱
        groupNum = len(groupIntervals)
        while(len(groupIntervals)>max_interval):   #the termination condition: the number of intervals is equal to the pre-specified threshold
            # in each step of iteration, we calcualte the chi-square value of each atttribute
            chisqList = []
            for interval in groupIntervals:
                df2 = regroup.loc[regroup[col].isin(interval)]
                chisq = Chi2(df2, 'total','bad',overallRate)
                chisqList.append(chisq)
            #find the interval corresponding to minimum chi-square, and combine with the neighbore with smaller chi-square
            min_position = chisqList.index(min(chisqList))
            if min_position == 0:## 如果最小位置为0,则要与其结合的位置为１
                combinedPosition = 1
            elif min_position == groupNum - 1:
                combinedPosition = min_position -1
            else:## 如果在中间，则选择左右两边卡方值较小的与其结合
                if chisqList[min_position - 1]<=chisqList[min_position + 1]:
                    combinedPosition = min_position - 1
                else:
                    combinedPosition = min_position + 1
            groupIntervals[min_position] = groupIntervals[min_position]+groupIntervals[combinedPosition]
            # after combining two intervals, we need to remove one of them
            groupIntervals.remove(groupIntervals[combinedPosition])
            groupNum = len(groupIntervals)
        groupIntervals = [sorted(i) for i in groupIntervals]　## 对每组的数据安从小到大排序
        cutOffPoints = [i[-1] for i in groupIntervals[:-1]]　## 提取出每组的最大值，也就是分割点
        return cutOffPoints

以卡方阈值作为终止分箱条件：

def ChiMerge_MinChisq(df, col, target, confidenceVal = 3.841):
    '''
    :param df: the dataframe containing splitted column, and target column with 1-0
    :param col: splitted column
    :param target: target column with 1-0
    :param confidenceVal: the specified chi-square thresold, by default the degree of freedom is 1 and using confidence level as 0.95
    :return: the splitted bins
    '''
    colLevels = set(df[col])
    total = df.groupby([col])[target].count()
    total = pd.DataFrame({'total':total})
    bad = df.groupby([col])[target].sum()
    bad = pd.DataFrame({'bad':bad})
    regroup =  total.merge(bad,left_index=True,right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)
    N = sum(regroup['total'])
    B = sum(regroup['bad'])
    overallRate = B*1.0/N
    colLevels =sorted(list(colLevels))
    groupIntervals = [[i] for i in colLevels]
    groupNum  = len(groupIntervals)
    while(1):   #the termination condition: all the attributes form a single interval; or all the chi-square is above the threshould
        if len(groupIntervals) == 1:
            break
        chisqList = []
        for interval in groupIntervals:
            df2 = regroup.loc[regroup[col].isin(interval)]
            chisq = Chi2(df2, 'total','bad',overallRate)
            chisqList.append(chisq)
        min_position = chisqList.index(min(chisqList))
        if min(chisqList) >=confidenceVal:
            break
        if min_position == 0:
            combinedPosition = 1
        elif min_position == groupNum - 1:
            combinedPosition = min_position -1
        else:
            if chisqList[min_position - 1]<=chisqList[min_position + 1]:
                combinedPosition = min_position - 1
            else:
                combinedPosition = min_position + 1
        groupIntervals[min_position] = groupIntervals[min_position]+groupIntervals[combinedPosition]
        groupIntervals.remove(groupIntervals[combinedPosition])
        groupNum = len(groupIntervals)
    return groupIntervals

无监督分箱法:

等距划分、等频划分

等距分箱
　　从最小值到最大值之间,均分为 N 等份, 这样, 如果 A,B 为最小最大值, 则每个区间的长度为 W=(B−A)/N , 则区间边界值为A+W,A+2W,…A+(N−1)W 。这里只考虑边界，每个等份里面的实例数量可能不等。
　　
等频分箱
　　区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。
　　
以上两种算法的弊端
　　比如,等宽区间划分,划分为5区间,最高工资为50000,则所有工资低于10000的人都被划分到同一区间。等频区间可能正好相反,所有工资高于50000的人都会被划分到50000这一区间中。这两种算法都忽略了实例所属的类型,落在正确区间里的偶然性很大。

我们对特征进行分箱后，需要对分箱后的每组（箱）进行woe编码，然后才能放进模型训练。

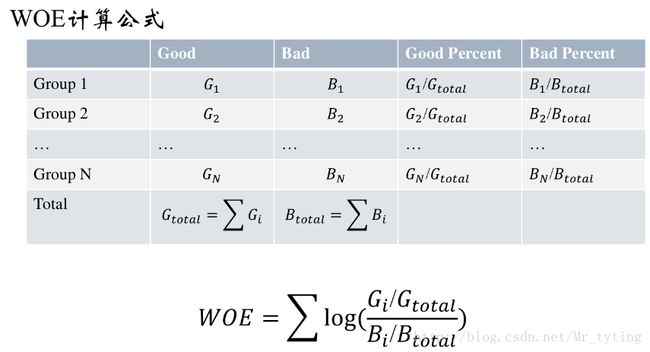
WOE编码

WOE(weight of evidence, 证据权重)

一种有监督的编码方式,将预测类别的集中度的属性作为编码的数值

优势
　　将特征的值规范到相近的尺度上。
　　(经验上讲,WOE的绝对值波动范围在0.1~3之间)。
　　具有业务含义。
　　
缺点
　　需要每箱中同时包含好、坏两个类别。

特征信息度

IV(Information Value), 衡量特征包含预测变量浓度的一种指标

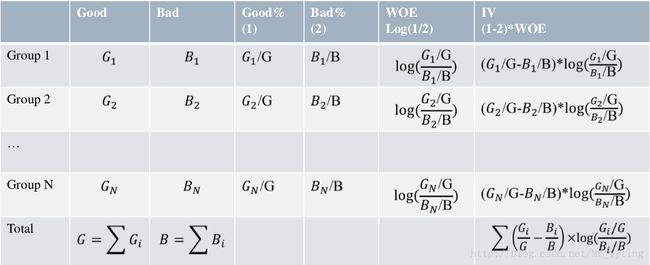
　特征信息度解构：
　
　其中Gi,Bi表示箱i中好坏样本占全体好坏样本的比例。
　WOE表示两类样本分布的差异性。
　(Gi-Bi)：衡量差异的重要性。

特征信息度的作用
　选择变量：

• 非负指标
• 高IV表示该特征和目标变量的关联度高
• 目标变量只能是二分类
• 过高的IV,可能有潜在的风险
• 特征分箱越细,IV越高
• 常用的阈值有:
  <=0.02: 没有预测性,不可用
  0.02 to 0.1: 弱预测性
  0.1 to 0.2: 有一定的预测性
  0.2 +: 高预测性

注意上面说的IV是指一个变量里面所有箱的IV之和。

计算WOE和IV代码：

def CalcWOE(df, col, target):
    '''
    :param df: dataframe containing feature and target
    :param col: 注意col这列已经经过分箱了，现在计算每箱的WOE和总的IV。
    :param target: good/bad indicator
    :return: 返回每箱的WOE(字典类型）和总的IV之和。
    '''
    total = df.groupby([col])[target].count()
    total = pd.DataFrame({'total': total})
    bad = df.groupby([col])[target].sum()
    bad = pd.DataFrame({'bad': bad})
    regroup = total.merge(bad, left_index=True, right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)
    N = sum(regroup['total'])
    B = sum(regroup['bad'])
    regroup['good'] = regroup['total'] - regroup['bad']
    G = N - B
    regroup['bad_pcnt'] = regroup['bad'].map(lambda x: x*1.0/B)
    regroup['good_pcnt'] = regroup['good'].map(lambda x: x * 1.0 / G)
    regroup['WOE'] = regroup.apply(lambda x: np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1)
    WOE_dict = regroup[[col,'WOE']].set_index(col).to_dict(orient='index')
    IV = regroup.apply(lambda x: (x.good_pcnt-x.bad_pcnt)*np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1)
    IV = sum(IV)
    return {"WOE": WOE_dict, 'IV':IV}

那么可能有人会问，以上都是有监督的分箱，有监督的WOE编码，如何能将这些有监督的方法应用到预测集上呢？
　　
　　我们观察下有监督的卡方分箱法和有监督的woe编码的计算公式不难发现，其计算结果都是以一个比值结果呈现（卡方分箱法：(坏样本数量-期望坏样本数量)/期望坏样本数量的比值形式；有监督的woe类似），比如我们发现预测集里面好坏样本不平衡，需要对坏样本进行一个欠采样或者是好样本进行过采样，只要是一个均匀采样，理论上这个有监督的卡方分箱的比值结果是不变的，其woe的比值结果也是不变的。即预测集上的卡方分组和woe编码和训练集上一样。
　　
　　那么，在训练集中我们对一个连续型变量进行分箱以后，对照这这个连续型变量每个值，如果这个值在某个箱中，那么就用这个箱子的woe编码代替他放进模型进行训练。

在预测集中类似，但是预测集中的这个连续型变量的某个值可能不在任一个箱中，比如在训练集中我对[x1,x2]分为一箱，[x3,x4]分为一箱，预测集中这个连续变量某个值可能为(x2+x3)/2即不在任意一箱中，如果把[x1,x2]分为一箱，那么这一箱的变量应该是x1<=x< x2；第二箱应该是x2<=x< x4等等。***即预测集中连续变量某一个值大于等于第i-1个箱的最大值，小于第ｉ个箱子的最大值，那么这个变量就应该对应第ｉ个箱子。***这样分箱就覆盖所有训练样本外可能存在的值。预测集中任意的一个值都可以找到对应的箱，和对应的woe编码。

def AssignBin(x, cutOffPoints):
    '''
    :param x: the value of variable
    :param cutOffPoints: 每组的最大值，也就是分割点
    :return: bin number, indexing from 0
    for example, if cutOffPoints = [10,20,30], if x = 7, return Bin 0. If x = 35, return Bin 3
    '''
    numBin = len(cutOffPoints) + 1
    if x<=cutOffPoints[0]:
        return 'Bin 0'
    elif x > cutOffPoints[-1]:
        return 'Bin {}'.format(numBin-1)
    else:
        for i in range(0,numBin-1):
            if cutOffPoints[i] < x <=  cutOffPoints[i+1]:
                return 'Bin {}'.format(i+1)

如果我们发现分箱以后能完全能区分出好坏样本，那么得注意了这个连续变量会不会是个事后变量。

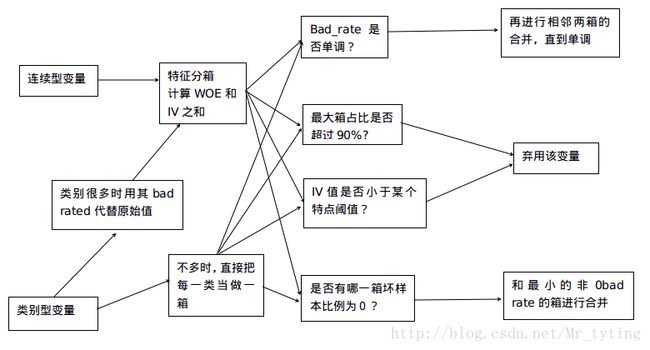
分箱的注意点

对于连续型变量做法:

• 使用ChiMerge进行分箱
• 如果有特殊值，把特殊值单独分为一组，例如把-1单独分为一箱。
• 计算这个连续型变量的每个值属于那个箱子，得出箱子编号。以所属箱子编号代替原始值。

def AssignBin(x, cutOffPoints):
    '''
    :param x: the value of variable
    :param cutOffPoints: the ChiMerge result for continous variable
    :return: bin number, indexing from 0
    for example, if cutOffPoints = [10,20,30], if x = 7, return Bin 0. If x = 35, return Bin 3
    '''
    numBin = len(cutOffPoints) + 1
    if x<=cutOffPoints[0]:
        return 'Bin 0'
    elif x > cutOffPoints[-1]:
        return 'Bin {}'.format(numBin-1)
    else:
        for i in range(0,numBin-1):
            if cutOffPoints[i] < x <=  cutOffPoints[i+1]:
                return 'Bin {}'.format(i+1)

• 检查分箱以后每箱的bad_rate的单调性，如果不满足，那么继续进行相邻的两箱合并，知道bad_rate单调为止。(可以放宽到U型)

## determine whether the bad rate is monotone along the sortByVar
def BadRateMonotone(df, sortByVar, target):
	# df[sortByVar]这列数据已经经过分箱
    df2 = df.sort([sortByVar])
    total = df2.groupby([sortByVar])[target].count()
    total = pd.DataFrame({'total': total})
    bad = df2.groupby([sortByVar])[target].sum()
    bad = pd.DataFrame({'bad': bad})
    regroup = total.merge(bad, left_index=True, right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)
    combined = zip(regroup['total'],regroup['bad'])
    badRate = [x[1]*1.0/x[0] for x in combined]
    badRateMonotone = [badRate[i]

上述过程是收敛的,因为当箱数为2时,bad rate自然单调

• 检查最大箱，如果最大箱里面数据数量占总数据的90%以上，那么弃用这个变量

def MaximumBinPcnt(df,col):
    N = df.shape[0]
    total = df.groupby([col])[col].count()
    pcnt = total*1.0/N
    return max(pcnt)

对于类别型变量：

• 当类别数较少时,原则上不需要分箱
• 否则，当类别较多时，以bad rate代替原有值，转成连续型变量再进行分箱计算。

def BadRateEncoding(df, col, target):
    '''
    :param df: dataframe containing feature and target
    :param col: the feature that needs to be encoded with bad rate, usually categorical type
    :param target: good/bad indicator
    :return: the assigned bad rate to encode the categorical fature
    '''
    total = df.groupby([col])[target].count()
    total = pd.DataFrame({'total': total})
    bad = df.groupby([col])[target].sum()
    bad = pd.DataFrame({'bad': bad})
    regroup = total.merge(bad, left_index=True, right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)
    regroup['bad_rate'] = regroup.apply(lambda x: x.bad*1.0/x.total,axis = 1)
    br_dict = regroup[[col,'bad_rate']].set_index([col]).to_dict(orient='index')
    badRateEnconding = df[col].map(lambda x: br_dict[x]['bad_rate'])
    return {'encoding':badRateEnconding, 'br_rate':br_dict}

• 否则， 检查最大箱，如果最大箱里面数据数量占总数据的90%以上，那么弃用这个变量

• 当某个或者几个类别的bad rate为0时,需要和最小的非0bad rate的箱进行合并。

### If we find any categories with 0 bad, then we combine these categories with that having smallest non-zero bad rate
def MergeBad0(df,col,target):
    '''
     :param df: dataframe containing feature and target
     :param col: the feature that needs to be calculated the WOE and iv, usually categorical type
     :param target: good/bad indicator
     :return: WOE and IV in a dictionary
     '''
    total = df.groupby([col])[target].count()
    total = pd.DataFrame({'total': total})
    bad = df.groupby([col])[target].sum()
    bad = pd.DataFrame({'bad': bad})
    regroup = total.merge(bad, left_index=True, right_index=True, how='left')
    regroup.reset_index(level=0, inplace=True)
    regroup['bad_rate'] = regroup.apply(lambda x: x.bad*1.0/x.total,axis = 1)
    regroup = regroup.sort_values(by = 'bad_rate')
    col_regroup = [[i] for i in regroup[col]]
    for i in range(regroup.shape[0]):
        col_regroup[1] = col_regroup[0] + col_regroup[1]
        col_regroup.pop(0)
        if regroup['bad_rate'][i+1] > 0:
            break
    newGroup = {}
    for i in range(len(col_regroup)):
        for g2 in col_regroup[i]:
            newGroup[g2] = 'Bin '+str(i)
    return newGroup

• 当该变量可以完全区分目标变量时,需要认真检查该变量的合理性。（可能是事后变量）

单变量分析

• 用IV检验该变量有效性（一般阈值区间在(0.0.2，0.8)）

iv_threshould = 0.02
## k,v分别表示col,col对应的这列的IV值。
varByIV = [k for k, v in var_IV.items() if v > iv_threshould]
## WOE_dict字典中包含字典。
WOE_encoding = []
for k in varByIV:
    if k in trainData.columns:
        trainData[str(k)+'_WOE'] = trainData[k].map(lambda x: WOE_dict[k][x]['WOE'])
        WOE_encoding.append(str(k)+'_WOE')
    elif k+str('_Bin') in trainData.columns:
        k2 = k+str('_Bin')
        trainData[str(k) + '_WOE'] = trainData[k2].map(lambda x: WOE_dict[k][x]['WOE'])
        WOE_encoding.append(str(k) + '_WOE')
    else:
        print "{} cannot be found in trainData"

• 连续变量bad rate的单调性(可以放宽到U型)
• 单一区间的占比不宜过高（一般不能超过90%，如果超过则弃用这个变量）

多变量分析

变量的两两相关性，当相关性高时,只能保留一个:

• 可以选择IV高的留下
• 或者选择分箱均衡的留下（后期评分得分会均匀）

#### we can check the correlation matrix plot
col_to_index = {WOE_encoding[i]:'var'+str(i) for i in range(len(WOE_encoding))}
#sample from the list of columns, since too many columns cannot be displayed in the single plot
corrCols = random.sample(WOE_encoding,15)
sampleDf = trainData[corrCols]
for col in corrCols:
    sampleDf.rename(columns = {col:col_to_index[col]}, inplace = True)
scatter_matrix(sampleDf, alpha=0.2, figsize=(6, 6), diagonal='kde')

#alternatively, we check each pair of independent variables, and selected the variabale with higher IV if they are highly correlated
compare = list(combinations(varByIV, 2))## 从varByIV随机的进行两两组合
removed_var = []
roh_thresould = 0.8
for pair in compare:
    (x1, x2) = pair
    roh = np.corrcoef([trainData[str(x1)+"_WOE"],trainData[str(x2)+"_WOE"]])[0,1]
    if abs(roh) >= roh_thresould:
        if var_IV[x1]>var_IV[x2]:## 选IV大的留下
            removed_var.append(x2)
        else:
            removed_var.append(x1)

多变量分析：变量的多重共线性
　通常用VIF来衡量，要求VIF<10:
　

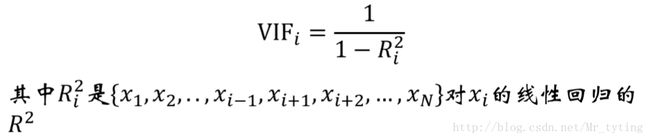
import numpy as np
from sklearn.linear_model  import LinearRegression


selected_by_corr=[i for i in varByIv if i not in removed_var]
for i in range(len(selected_by_corr)):
    x0=trainData[selected_by_corr[i]+'_WOE']
    x0=np.array(x0)
    X_Col=[k+'_WOE' for k in selected_by_corr if k!=selected_by_corr[i]]
    X=trainData[X_Col]
    X=np.array(X)
    regr=LinearRegression()
    clr=regr.fit(X,x0)
    x_pred=clr.predit(X)
    R2=1-((x_pred-x0)**2).sum()/((x0-x0.mean())**2).sum()
    vif=1/(1-R2)
    print "The vif for {0} is {1}".format(selected_by_corr[i],vif)

当发现vif>10时，需要逐一剔除变量，当剔除变量Xk时，发现vif<10时，此时剔除{Xi,Xk}中IV小的那个变量。
通常情况下，计算vif这一步不是必须的，在进行单变量处理以后，放进逻辑回归模型进行训练预测，如果效果非常不好时，才需要做多变量分析，消除多重共线性。

本篇博文总结：