算法学习24-哈希表&&设计RandomPool结构&&认识布隆过滤器&&认识一致性哈希&&岛问题&&认识并查集结构

题目一：哈希表相关基础知识

什么是哈希表？

哈希表（Hash table，也叫散列表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

记录的存储位置=f(关键字)

这里的对应关系f称为散列函数，又称为哈希（Hash函数），采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表或哈希表（Hash table）。

哈希表hashtable(key，value) 就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里。（或者：把任意长度的输入（又叫做预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。）
而当使用哈希表进行查询的时候，就是再次使用哈希函数将key转换为对应的数组下标，并定位到该空间获取value，如此一来，就可以充分利用到数组的定位性能进行数据定位。

数组的特点是：寻址容易，插入和删除困难；

而链表的特点是：寻址困难，插入和删除容易。

那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表，哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法——拉链法，我们可以理解为“链表的数组”，如图：

左边很明显是个数组，数组的每个成员包括一个指针，指向一个链表的头，当然这个链表可能为空，也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去，也是根据这些特征，找到正确的链表，再从链表中找出这个元素。

Hash的应用

1、Hash主要用于信息安全领域中加密算法，它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说，Hash就是找到一种数据内容和数据存放地址之间的映射关系。

2、查找：哈希表，又称为散列，是一种更加快捷的查找技术。我们之前的查找，都是这样一种思路：集合中拿出来一个元素，看看是否与我们要找的相等，如果不等，缩小范围，继续查找。而哈希表是完全另外一种思路：当我知道key值以后，我就可以直接计算出这个元素在集合中的位置，根本不需要一次又一次的查找！

举一个例子，假如我的数组A中，第i个元素里面装的key就是i，那么数字3肯定是在第3个位置，数字10肯定是在第10个位置。哈希表就是利用利用这种基本的思想，建立一个从key到位置的函数，然后进行直接计算查找。

3、Hash表在海量数据处理中有着广泛应用。

Hash Table的查询速度非常的快，几乎是O(1)的时间复杂度。

hash就是找到一种数据内容和数据存放地址之间的映射关系。

散列法：元素特征转变为数组下标的方法。

我想大家都在想一个很严重的问题：“如果两个字符串在哈希表中对应的位置相同怎么办？”,毕竟一个数组容量是有限的，这种可能性很大。解决该问题的方法很多，我首先想到的就是用“链表”。我遇到的很多算法都可以转化成链表来解决，只要在哈希表的每个入口挂一个链表，保存所有对应的字符串就OK了。

散列表的查找步骤
当存储记录时，通过散列函数计算出记录的散列地址
当查找记录时，我们通过同样的是散列函数计算记录的散列地址，并按此散列地址访问该记录

关键字——散列函数（哈希函数）——散列地址

优点：一对一的查找效率很高；

缺点：一个关键字可能对应多个散列地址；需要查找一个范围时，效果不好。

散列冲突：不同的关键字经过散列函数的计算得到了相同的散列地址。

好的散列函数=计算简单+分布均匀（计算得到的散列地址分布均匀）

哈希表是种数据结构，它可以提供快速的插入操作和查找操作。

优缺点

优点：不论哈希表中有多少数据，查找、插入、删除（有时包括删除）只需要接近常量的时间即0(1）的时间级。实际上，这只需要几条机器指令。

哈希表运算得非常快，在计算机程序中，如果需要在一秒种内查找上千条记录通常使用哈希表（例如拼写检查器)哈希表的速度明显比树快，树的操作通常需要O(N)的时间级。哈希表不仅速度快，编程实现也相对容易。

如果不需要有序遍历数据，并且可以提前预测数据量的大小。那么哈希表在速度和易用性方面是无与伦比的。

缺点：它是基于数组的，数组创建后难于扩展，某些哈希表被基本填满时，性能下降得非常严重，所以程序员必须要清楚表中将要存储多少数据（或者准备好定期地把数据转移到更大的哈希表中，这是个费时的过程）。

元素特征转变为数组下标的方法就是散列法。散列法当然不止一种，下面列出三种比较常用的：

1，除法散列法
最直观的一种，上图使用的就是这种散列法，公式：
index = value % 16
学过汇编的都知道，求模数其实是通过一个除法运算得到的，所以叫“除法散列法”。

2，平方散列法
求index是非常频繁的操作，而乘法的运算要比除法来得省时（对现在的CPU来说，估计我们感觉不出来），所以我们考虑把除法换成乘法和一个位移操作。公式：
index = (value * value) >> 28 （右移，除以2^28。记法：左移变大，是乘。右移变小，是除。）
如果数值分配比较均匀的话这种方法能得到不错的结果，但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题，value如果很大，value * value不会溢出吗？答案是会的，但我们这个乘法不关心溢出，因为我们根本不是为了获取相乘结果，而是为了获取index。

3，斐波那契（Fibonacci）散列法

平方散列法的缺点是显而易见的，所以我们能不能找出一个理想的乘数，而不是拿value本身当作乘数呢？答案是肯定的。

1，对于16位整数而言，这个乘数是40503
2，对于32位整数而言，这个乘数是2654435769
3，对于64位整数而言，这个乘数是11400714819323198485

这几个“理想乘数”是如何得出来的呢？这跟一个法则有关，叫黄金分割法则，而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列，即如此形式的序列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610， 987, 1597, 2584, 4181, 6765, 10946，…。另外，斐波那契数列的值和太阳系八大行星的轨道半径的比例出奇吻合。

对我们常见的32位整数而言，公式： 
        index = (value * 2654435769) >> 28

如果用这种斐波那契散列法的话，那上面的图就变成这样了：

注：用斐波那契散列法调整之后会比原来的取摸散列法好很多。

适用范围
快速查找，删除的基本数据结构，通常需要总数据量可以放入内存。

基本原理及要点
hash函数选择，针对字符串，整数，排列，具体相应的hash方法。
碰撞处理，一种是open hashing，也称为拉链法；另一种就是closed hashing，也称开地址法，opened addressing。

散列冲突的解决方案：

1.建立一个缓冲区，把凡是拼音重复的人放到缓冲区中。当我通过名字查找人时，发现找的不对，就在缓冲区里找。

2.进行再探测。就是在其他地方查找。探测的方法也可以有很多种。

（1）在找到查找位置的index的index-1，index+1位置查找，index-2，index+2查找，依次类推。这种方法称为线性再探测。

（2）在查找位置index周围随机的查找。称为随机在探测。

（3）再哈希。就是当冲突时，采用另外一种映射方式来查找。

这个程序中是通过取模来模拟查找到重复元素的过程。对待重复元素的方法就是再哈希：对当前key的位置+7。最后，可以通过全局变量来判断需要查找多少次。我这里通过依次查找26个英文字母的小写计算的出了总的查找次数。显然，当总的查找次数/查找的总元素数越接近1时，哈希表更接近于一一映射的函数，查找的效率更高。

扩展
d-left hashing中的d是多个的意思，我们先简化这个问题，看一看2-left hashing。2-left hashing指的是将一个哈希表分成长度相等的两半，分别叫做T1和T2，给T1和T2分别配备一个哈希函数，h1和h2。在存储一个新的key时，同 时用两个哈希函数进行计算，得出两个地址h1[key]和h2[key]。这时需要检查T1中的h1[key]位置和T2中的h2[key]位置，哪一个 位置已经存储的（有碰撞的）key比较多，然后将新key存储在负载少的位置。如果两边一样多，比如两个位置都为空或者都存储了一个key，就把新key 存储在左边的T1子表中，2-left也由此而来。在查找一个key时，必须进行两次hash，同时查找两个位置。

问题实例（海量数据处理）
我们知道hash 表在海量数据处理中有着广泛的应用，下面，请看另一道百度面试题：
题目：海量日志数据，提取出某日访问百度次数最多的那个IP。
方案：IP的数目还是有限的，最多2^32个，所以可以考虑使用hash将ip直接存入内存，然后进行统计。

题目二：设计RandomPool结构

题目 及其要求

设计一种结构，在该结构中有如下三个功能： 
1.insert(key)：将某个key加入到该结构，做到不重复加入。 
2.delete(key)：将原本在结构中的某个key移除。 
3.getRandom()：等概率随机返回结构中的任何一个key。 

要求

Insert、delete和getRandom方法的时间复杂度都是 O(1)

算法实现

• 用两个哈希表，存入时同时存人到哈希表中
• 删除数据时，及通过key去寻找value值
• 要做到绝对的随机，及用 rand() % size

代码实现

#include 
#include 
#include 

class RandomPool {
public:
    std::unordered_map keyIndexMap;
    std::unordered_map indexKeyMap;
    int size;
    RandomPool(): size(0) {}   // default constructor

    void insertKey(std::string key) {
        if (keyIndexMap.find(key) == keyIndexMap.end()) {   // if don't have key
            keyIndexMap.emplace(key, size);  // we can also insert({key, size}) instead
            indexKeyMap.emplace(size, key);
            size++;
        }
    }

    void deleteKey(std::string key) {
        if (keyIndexMap.find(key) != keyIndexMap.end()) {  // if we have key
            int deleteIndex = keyIndexMap.at(key);  // find we we want to delete the index
            int lastIndex = --size;  // last index
            std::string lastKey = indexKeyMap.at(lastIndex);    // find the last key
            keyIndexMap.erase(key);
            keyIndexMap.erase(lastKey);
            indexKeyMap.erase(deleteIndex);
            indexKeyMap.erase(lastIndex);
            keyIndexMap.emplace(lastKey, deleteIndex);
            indexKeyMap.emplace(deleteIndex, lastKey);
        }
    }

    std::string getRandomKey() {
        int random = rand() % size;     // get [0, size-1]
        return indexKeyMap.at(random);  // we can also use indexKeyMap[random] instead
    }
};
int main()
{
    RandomPool randomPool;
    randomPool.insertKey("A");
    randomPool.insertKey("B");
    randomPool.insertKey("C");
    std::cout << "===================Insert key===================" << std::endl;
    std::cout << "keyIndexMap: " << std::endl;
    for (auto& it: randomPool.keyIndexMap) {
        std::cout << it.first << ": " << it.second << std::endl;
    }
    std::cout << "indexKeyMap: " << std::endl;
    for (auto it = randomPool.indexKeyMap.begin(); it != randomPool.indexKeyMap.end(); ++it) {
        std::cout << it->first << ": " << it->second << std::endl;
    }
    std::cout << "===================Random key===================" << std::endl;
    std::string randomKey1 = randomPool.getRandomKey();
    std::string randomKey2 = randomPool.getRandomKey();
    std::string randomKey3 = randomPool.getRandomKey();
    std::cout << "key1: " << randomKey1 << "\n" << "key2: "
              << randomKey2 << "\n" <<  "key3: " << randomKey3 << std::endl;

    std::cout << "===================Delete key===================" << std::endl;
    randomPool.deleteKey("A");  // delete "A"
    std::cout << "keyIndexMap: " << std::endl;
    for (auto& it: randomPool.keyIndexMap) {
        std::cout << it.first << ": " << it.second << std::endl;
    }
    std::cout << "indexKeyMap: " << std::endl;
    for (auto it = randomPool.indexKeyMap.begin(); it != randomPool.indexKeyMap.end(); ++it) {
        std::cout << it->first << ": " << it->second << std::endl;
    }
    std::cout << "==================After delete random key========" << std::endl;
    std::string randomKey11 = randomPool.getRandomKey();
    std::string randomKey22 = randomPool.getRandomKey();
    std::string randomKey33 = randomPool.getRandomKey();
    std::cout << "key1: " << randomKey11 << "\n" << "key2: "
              << randomKey22 << "\n" <<  "key3: " << randomKey33 << std::endl;
    return 0;
}

题目三：认识布隆过滤器

布隆过滤器用来做什么

布隆过滤器可用来判定一个元素是否属于一个集合，更严谨的讲是：它能100%确定一个元素不属于某个集合，但不能100%确定一个元素属于某个集合。
关于其使用场景，第一想到的是用来判定“是否需要执行高昂的操作”，比如访问网络或者磁盘上的某些资源。比如Google 的BitTable 和Apach HBase都使用布隆过滤器判断查询的数据是否存，来确定是否需要继续读取磁盘。再比如，用爬虫抓取网页时，有些网页会相互链接或者多个网页含有同一网页链接，所以使用布隆过滤器判断url是否爬取过了，来确定是否继续发起该url的访问。

布隆过滤器是怎么实现和使用的

布隆过滤器由两个部分组成：一个位数组和一组散列函数。为了初始化布隆过滤器，我们将位数组中的所有位设置为零。

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

当为集合增加一个元素时，我们将元素作为输入提供给散列函数。 每个散列函数将输出一个数组索引。 假设将字符串“hello”传递给两个散列函数f1，f2，这两个散列函数给出索引0和4，我们将位数组中的相应位设置为1：

[1, 0, 0, 0, 1, 0, 0, 0, 0, 0]

当查询一个元素时，我们将元素传给两个散列函数，获得两个索引后，检查数组中相应位的值：

• 如果两个值中有0，可能的索引值组合有（0，0）、（0，1）、（1，0），即可判定该元素不在集合中。所以，不一定需要检查所有函数返回位的值，如果发现至少有一个值是0，那么即可判定该元素不在集合中。比如我们要查询“word”是否属于集合，假设两个函数返回的索引是1和5。因为两个索引位值都是0，所以检查其中任意一个位都可以得出“word不属于集合“的结论。
• 如果两个值都是1，只可判定为“该元素可能在集合中”，因为散列函数可能会产生冲突。比如我们使用两个函数获取“bloom”的索引可能为1和9，获取“filter”的索引可能为5和7，而此时再去查询“word”，会因为1和9已被“bloom”和“filter”已经设置为1而产出冲突。因此，我们不能100%确定查询的元素在集合中。

​ 当去除一个元素集合时，因为“散列函数可能产生冲突”的问题，如果我们要重置希望删除元素的相应位，可能会误删具有相同索引位的其他元素，所以此时不需要（不容易）对位数组进行处理。

为什么布隆过滤器效率比较高

时间复杂度

• 添加元素时，由于不需要迭代位数组，而是简单的设置索引位的值，所以操作所花费的时间仅取决于散列函数的个数，所以对于对于k个哈希函数的布隆过滤器，添加元素的时间复杂度为O(k) 。
• 查询元素时，对于k个哈希函数的布隆过滤器，只需要在位数组中检查的索引数量有一个不变的上界，所以查询元素的时间复杂度也为O(k)。

空间复杂度

​ 由于不需要存储元素，只需依赖一定长度的位数组判断是否存在，并且数组长度的大小不也取决于集合中元素的多少，可以在误判率变大或效率变低的代价下减少存储（位数组）。

布隆过滤器有哪些缺点

主要缺点是有一定的误判率和删除比较困难，所以随着存入集合的元素的增加，误判率也随之增加。误判率大小和三个指标有关：位数组长度m、集合长度n、散列函数个数k，其之间关系可以参考文献 ，该文献证明了对于给定的m、n，当 k = ln(2)* m/n 时误判率是最小的。

题目四：认识一致性哈希

直到现在为止，一致性哈希也没有一个非常明确的定义，多数文献还是从其应用场景之上对一致性哈希进行描述。“哈希”想必大家都已经了解，问题是何为“一致性”？

一致性

在讨论一致性哈希之前，先认识下“非一致性哈希”，显然HashMap属于此列。

当使用HashMap时，key被均匀地映射到数组之上，映射方法就是利用key的hash与数组长度取模(通过&运算)。

当put的数据超过负载因子loadFactor×2Len时，HashMap会按照2被的容量扩容。新put进来的数据会通过与新数组的长度取模的方式进行映射。那之前已经映射的数据该怎么办？通过查看HashMap代码的resize方法会发现，每次扩容都会把之前的key重新映射。

所以对HashMap而言要想获得较好的性能必须要提前估计所放数据集合的大小，以设计合适的初始化容量和负载因子。

定义

但不是每个场景都像HashMap这么简单，比如在大型的P2P网络中存在上百万台Server，资源与Server的关系是以Key的形式映射而成，也就是说是一个大的HashMap，维护着每个Key在哪个Server之上，如果有新的节点加入或退出P2P网络，跟HashMap一样，也会导致映射关系的变化，显然不可能把所有的Key与Server的映射关系都调整一遍。这就需要一种方法，在哈希项发生变化是，不需要调整所有的节点，而达到继续维护哈希映射的关系。因此一致性哈希定义为：

“Consistent hashing is a scheme that provides hash table functionality in a way that the addition or removal of one slot does not significantly change the mapping of keys to slots”.

就是说，”一致性哈希，就是提供一个hashtable,它能在节点加入离开时不会导致映射关系的重大变化“。

实现

一致性哈希的定义除了描述一个定义或者一种想法并没有给出任何实现方面的描述，所有细化的问题都留给开发者去思考。但一般的实现思路如下：

• 假定哈希的均匀Key分布在一个环上，比如所有节点都通过SHA-1或MD5进行哈希映射
• 所有的节点也都分布在同一环上（比如Server的IP地址经过SHA-1）
• 每个节点只负责一部分Key，当节点加入、退出时只影响加入退出的节点和其邻居节点或者其他节点只有少量的Key受影响

假如有n个节点，m个key，当节点增加时大约有O(m/n)的节点需要移动。但一般一致性哈希需要满足下面几个条件才对实际系统有意义：

• 平衡性(Balance)：就是指哈希算法要均匀分布，不能有明显的映射规律，这对一般的哈希实现也是必须的
• 单调性(Monotonicity)：就是指有新节点加入时，已经存在的映射关系不能发生变化
• 分散性(Spread)：就是避免不同的内容映射到相同的位置和相同的内容映射到不同的位置

其实一致性哈希（哈希）有个明显的优点就是负载均衡，只要哈希函数设计得当，每个点就是对等的可以均匀地分布系统负载。

Memcached

看了上面的定义和实现可能还是比较迷茫，那就举个实际例子。

Memcached对大家应该不陌生，通过把Key映射到Memcached Server上，实现快速读取。我们可以动态对其节点增加，并未影响之前已经映射到内存的Key与memcached Server之间的关系，这就是因为使用了一致性哈希。

因为Memcached的哈希策略是在其客户端实现的，因此不同的客户端实现也有区别，以Spymemcache、Xmemcache为例，都是使用了KETAMA作为其实现。

KETAMA实现方式如下：

• 把Server的IP地址和端口进行MD5哈希，MD5的结果为一个160bit的数字，取其前32位作为一个Integer
• 把缓存对象的Key做MD5哈希，同样得到一个整数
• 可以设想，Server的整数会根据大小形成一个数字环，而Key的哈希则分布在这些数字上或中间
• 如果Server的哈希等于Key的哈希，则把Key存放在该Server上；否则，寻找第一个大于Key哈希的Server，用于存放Key
• 但有Server增加、删除时，只要变动周边的Server映射关系即可，不用全部重新哈希。之所以有这样优良的特性是因为，Server和Key采用了同样的值域

但是这样做的效果并不理想，原因是哈希虽然是随机的，但往往随机的不如人意，尤其是在Server节点数量上的情况下，Server不会均匀分布在哈希环上，这会导致哈希不均匀，某些Server会承担很多的Key，而另一些会很少，如图：

绝大多数Key会映射到Server1，因此KETAMA引入了虚节点的概念，就是假象每个Server映射到N个节点（根据测试N在100～200时较优化），但Key的哈希映射到这N个节点时实际都有该Server来托管。这样做的意义在于，使因为实际节点少而导致大片未被映射的区别有虚节点去填充，从而使实节点有了处理本不属于自己区间的Key。有虚节点后的环如下：

新增的同名节点即为虚节点。

还有最后一个问题，虚节点是如何产生的呢？也非常简单，就是在每个Server加个后缀，在做MD5哈希，取其32位。

题目五:岛问题

题目 及其要求

一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右 四个位置相连，如果有一片1连在一起，这个部分叫做一个岛，求一个 矩阵中有多少个岛？

举例：

0 0 1 0 1 0 
1 1 1 0 1 0 
1 0 0 1 0 0 
0 0 0 0 0 0 

这个矩阵中有三个岛。

算法实现

简单的遍历即可，在处理是否被包围的时候，只需要判断该数的上，下，左右，是否都大于等于1，即有1包围即可。

代码实现

#include 
using namespace std;

int island[100][100];
int Number;

int jude(int x, int y)
{
//判断行
    int tmp = 0;
    for (int i = 0; i < y; i++)
        tmp += island[x][i];
    if (tmp < 1)
        return 0;
    else{
        tmp = 0;
        for (int i = y; i < Number; i++)
            if (i == y)
                continue;
            else
            {
                tmp += island[x][i];
            }
        if (tmp < 1)
            return 0;
    }
    
    tmp = 0;
    for (int i = 0; i < x; i++)
        tmp += island[i][y];
    if (tmp < 1)
        return 0;
    else{
        tmp = 0;
        for (int i = x; i < Number; i++)
            if (i == x)
                continue;
            else
            {
                tmp += island[i][y];
            }
        if (tmp < 1)
            return 0;
    }
    return 1;
}
int main()
{
    cin >> Number;
    int Temps;
    int count = 0;
    int i = 0;
    getchar();
    for (i = 0; i < Number; i++)
        for (int j = 0; j < Number; j++)
            cin >> island[i][j];
    int ares = 0;
    for (i = 0; i < Number; i++)
        for (int j = 0; j < Number; j++)
        {
            if (island[i][j] == 0)
            {
                if (jude(i, j))
                    ares++;
            }
        }
    cout << ares<

题目六:认识并查集结构

如何有趣的理解并查集结构

话说江湖上散落着各式各样的大侠，有上千个之多。他们没有什么正当职业，整天背着剑在外面走来走去，碰到和自己不是一路人的，就免不了要打一架。但大侠们有一个优点就是讲义气，绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”，只要是能通过朋友关系串联起来的，不管拐了多少个弯，都认为是自己人。

这样一来，江湖上就形成了一个一个的群落，通过两两之间的朋友关系串联起来。而不在同一个群落的人，无论如何都无法通过朋友关系连起来，于是就可以放心往死了打。但是两个原本互不相识的人，如何判断是否属于一个朋友圈呢？

我们可以在每个朋友圈内推举出一个比较有名望的人，作为该圈子的代表人物，这样，每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人，就可以确定敌友关系了。 但是还有问题啊，大侠们只知道自己直接的朋友是谁，很多人压根就不认识队长，要判断自己的队长是谁，只能漫无目的的通过朋友的朋友关系问下去：“你是不是队长？你是不是队长？” 这样一来，队长面子上挂不住了，而且效率太低，还有可能陷入无限循环中。

于是队长下令，重新组队。队内所有人实行分等级制度，形成树状结构，我队长就是根节点，下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候，只要一层层向上问，直到最高层，就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通，至于他们是如何连通的，以及每个圈子内部的结构是怎样的，甚至队长是谁，并不重要。所以我们可以放任队长随意重新组队，只要不搞错敌友关系就好了。于是，门派产生了。

——博客：数据结构4——并查集（入门）

什么是并查集

**并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。**一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

使用并查集时，首先会存在一组不相交的动态集合[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RipHRman-1581951045790)(https://math.jianshu.com/math?formula=S%20%3D%20%5Cleft%5C%7B%20%7B%7BS_1%7D%2C%7BS_2%7D%2C%20%5Ccdots%20%2C%7BS_k%7D%7D%20%5Cright%5C%7D)]，一般都会使用一个整数表示集合中的一个元素。

每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表，称为集合的代表元。

每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级的。

---

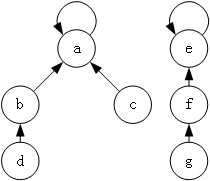
并查集的实现原理也比较简单，就是使用树来表示集合，树的每个节点就表示集合中的一个元素，树根对应的元素就是该集合的代表元，如图 1 所示。

图中有两棵树，分别对应两个集合，其中第一个集合为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C3qm9ndP-1581951045791)(https://math.jianshu.com/math?formula=%5Cleft%5C%7B%20a%2C%20b%2C%20c%2C%20d%20%5Cright%5C%7D)]，代表元素是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PYyut0pm-1581951045792)(https://math.jianshu.com/math?formula=a)]；第二个集合为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WpqQ8DxQ-1581951045793)(https://math.jianshu.com/math?formula=%5Cleft%5C%7B%20e%2C%20f%2C%20g%20%5Cright%5C%7D)]，代表元素是 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lVt9Rx2A-1581951045794)(https://math.jianshu.com/math?formula=e)]。

并查集的基本操作有三个：

• makeSet(s)：建立一个新的并查集，其中包含 s 个单元素集合。【初始化】
• unionSet(x, y)：把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。【合并】
• find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。【查找】

这也就是为什么叫并查集的原因，顾名思义，就是为了进行查和并操作。

并查集的初始化操作

树的节点表示集合中的元素，指针表示指向父节点的指针，根节点的指针指向自己，表示其没有父节点。

#define N 105
int parent[N];// 树型结构的根节点
int r[N];// 树的秩 

//初始化
int init(int n)     //对n个结点初始化
{
    for(int i = 0; i < n; i++)
    {
        parent[i] = i;     // 每个结点的上级都是自己
        r[i] = 0;    // 每个结点构成的树的秩为0
    }
}

并查集的查找操作

沿着每个结点的父节点不断向上查找，最终就可以找到该树的根结点，即该集合的代表元素。

int find_parent(int x) // 查找结点x的根结点
{
    if(parent[x] == x) // 递归出口：x的上级为x本身，即x为根结点
    {        
        return x;      
    }
    return find_parent(parent[x]);// 递归查找
}

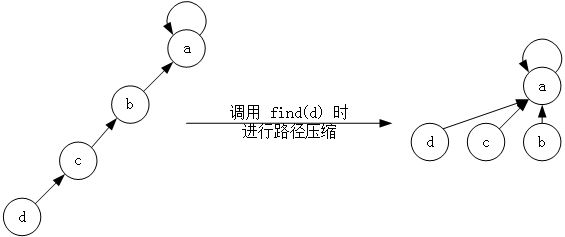
通过下面的图，我们发现，普通的查找过程相对较麻烦，例如寻找d结点的根节点，我们需要通过**[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SF43E3C3-1581951045795)(https://math.jianshu.com/math?formula=d-%3Ec-%3Eb-%3Ea)]**才能最终找到。

但是，如果我们使用路径压缩算法，那么只需要查找一次，就能确定d结点的结点，即**[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rR3Gu8S9-1581951045796)(https://math.jianshu.com/math?formula=d-%3Ea)]。**

//【递归版本】
// 改进查找算法：完成路径压缩，将x的上级直接变为根结点，那么树的高度就会大大降低
int find_parent(int x) // 查找结点x的根结点
{
    if(parent[x] == x) // 递归出口：x的上级为x本身，即x为根结点
    {        
        return x;      
    }
    return parent[x] = find_parent(parent[x]);// 递归查找，此代码相当于先找到根结点rootx，然后pre[x]=rootx
}

//【路径压缩的另一种写法】
//【个人更偏向于这种写法】 
int find_parent(int x)
{
    if(parent[x]!=x)parent[x]=find_parent(parent[x]);
    return parent[x];
} 

并查集的合并操作

朴素合并

并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根。

void unite(int x,int y)
{
    int root_x, root_y;
    root_x = find_parent(x);
    root_y = find_parent(y);
    if(root_x!=root_y)parent[root_y]=root_x;
}

按秩合并

也可以采用一种优化方法——按秩合并，注意初始化的时候需要将[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PkoIPNDA-1581951045798)(https://math.jianshu.com/math?formula=r%E6%95%B0%E7%BB%84)]全部置0。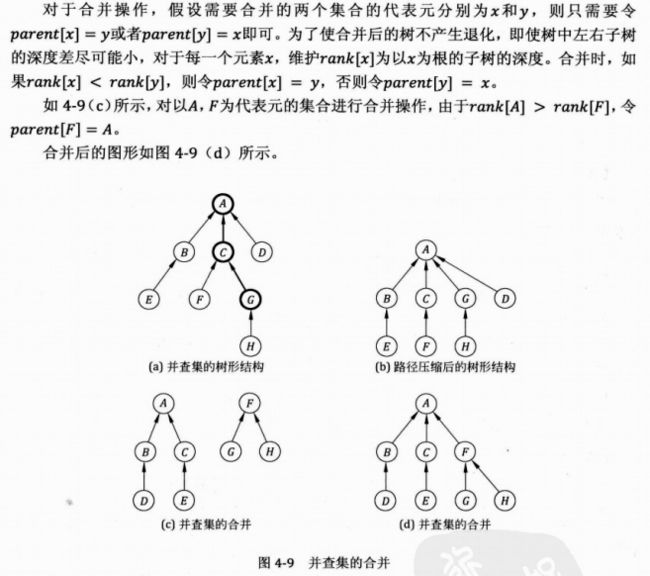

void unite(int x,int y)
{
    int root_x, root_y;
    root_x = find_parent(x);
    root_y = find_parent(y);
    // 属于同一个集合 
    if(root_x == root_y)return;
    // 属于不同集合 
    //令 y的根结点的上级为 root_x
    if(r[root_x] > r[root_y])parent[root_y] = root_x;         
    else
    {
        // 秩相等，合并之后秩需要加 1 
        if(r[root_x] == r[root_y])r[root_y]++;
        parent[root_x] = root_y;
    }
}

并查集的分析与用法：

时空复杂度

时间复杂度：

同时使用路径压缩、按秩（rank）合并优化的程序每个操作的平均时间仅为[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S2bJIaAU-1581951045800)(https://math.jianshu.com/math?formula=O(%5Calpha(n)]))，其中[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GxsLC0bF-1581951045800)(https://math.jianshu.com/math?formula=%5Calpha(n)])是[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6NuyLybY-1581951045801)(https://math.jianshu.com/math?formula=n%3Df(x)]%3DA(x%2Cx))的反函数，[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FwZ9hwCQ-1581951045802)(https://math.jianshu.com/math?formula=A)]是急速增加的阿克曼函数。因为[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-J6CNW3lq-1581951045802)(https://math.jianshu.com/math?formula=%5Calpha(n)])是其反函数，故**[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LyUQ9La0-1581951045803)(https://math.jianshu.com/math?formula=%5Calpha(n)])在[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w40f2NXx-1581951045803)(https://math.jianshu.com/math?formula=n)]十分巨大时还是小于 5。**因此，**平均运行时间是一个极小的常数。**实际上，这是渐近最优算法：Fredman 和 Saks 在 1989 年解释了[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FqypcjYz-1581951045804)(https://math.jianshu.com/math?formula=%5COmega(%5Calpha(n)]))的平均时间内可以获得任何并查集。

空间复杂度

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KtRadJz2-1581951045804)(https://math.jianshu.com/math?formula=O(n)])（n为元素个数）
按秩合并会多一个保存秩的辅助空间，即[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wtRfrBhG-1581951045805)(https://math.jianshu.com/math?formula=%E6%95%B0%E7%BB%84r)]。

——《维基百科：并查集》

用途：

• 判断是否是同一类：
  这个很简单，给定要判定的两个节点，find_parent()一下就可以了
• 判断有多少个类/是否连通：
  这个就基本上要遍历一下所有的节点，然后再把它们的父亲节点加入到set集合里，然后再统计一下个数即可。
• 最小生成树：Kruskal算法
  _parent()一下就可以了
• 判断有多少个类/是否连通：
  这个就基本上要遍历一下所有的节点，然后再把它们的父亲节点加入到set集合里，然后再统计一下个数即可。
• 最小生成树：Kruskal算法

参考资料

• 博客：算法模板学习专栏之并查集(一)入门（文字来源）
• 博客：数据结构4——并查集（入门）（图片、文字来源）【讲解很有意思的一篇博客】
• 博客：并查集（图片、文字来源）【推荐】
• 维基百科：并查集（文字来源）