AcWing 1170 排队布局

题目描述：

当排队等候喂食时，奶牛喜欢和它们的朋友站得靠近些。

农夫约翰有 N 头奶牛，编号从 1 到 N，沿一条直线站着等候喂食。

奶牛排在队伍中的顺序和它们的编号是相同的。

因为奶牛相当苗条，所以可能有两头或者更多奶牛站在同一位置上。

如果我们想象奶牛是站在一条数轴上的话，允许有两头或更多奶牛拥有相同的横坐标。

一些奶牛相互间存有好感，它们希望两者之间的距离不超过一个给定的数 L。

另一方面，一些奶牛相互间非常反感，它们希望两者间的距离不小于一个给定的数 D。

给出 ML 条关于两头奶牛间有好感的描述，再给出 MD 条关于两头奶牛间存有反感的描述。

你的工作是：如果不存在满足要求的方案，输出-1；如果 1 号奶牛和 N 号奶牛间的距离可以任意大，输出-2；否则，计算出在满足所有要求的情况下，1 号奶牛和 N 号奶牛间可能的最大距离。

输入格式

第一行包含三个整数 N,ML,MD。

接下来 ML 行，每行包含三个正整数 A,B,L，表示奶牛 A 和奶牛 B 至多相隔 L 的距离。

再接下来 MD 行，每行包含三个正整数 A,B,D，表示奶牛 A 和奶牛 B 至少相隔 D 的距离。

输出格式

输出一个整数，如果不存在满足要求的方案，输出-1；如果 1 号奶牛和 N 号奶牛间的距离可以任意大，输出-2；否则，输出在满足所有要求的情况下，1 号奶牛和 N 号奶牛间可能的最大距离。

数据范围

2≤N≤1000,
11≤ML,MD≤10^4,
1≤L,D≤10^6

输入样例：

4 2 1
1 3 10
2 4 20
2 3 3

输出样例：

27

分析：

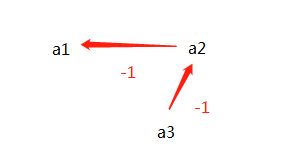
 本题同样是差分约束的问题，要求1到n之间可能的最大的距离，这使得我们更加深刻的理解了差分约束的思想。在AcWing 1169 糖果里，仔细的讲解了差分约束的基本思想，以及求不等式组的最大解需要求最短路，求最小解需要求最长路，这里不等式解的最大最小都是相对而言的。比如a2 <= a1 + 1,a3 <= a2 + 1，求最短路和最长路的建图如下图所示：

对于最短路而言，设起点a1 = 0，求得a2的最大值是1，a3的最大值是2；对于最长路而言，设a3 = 0，则a2的最小值是-1，a1的最小值是-2，所以所谓的最值都是相对的，本题求1到n之间的最大距离很能够体现这种相对的关系。下面梳理下已知的结论：对于同一个不等式组，最短路和最长路建图是完全不同的，边的大小互为相反数，方向相反，如果不等式组无解，即没有合法的一组解使得所有的不等式都成立，那么建立的最短路图中一定存在负环，建立的最长路的图中一定存在正环。如果不等式组有解，最短路求得的是最大解，最长路求得的是最小解。

要求1到n之间的距离，不妨设1号点的坐标就是0，从0出发到达终点n，要想距离最大，则n号点的解就要最大，所以需要求最短路。当然如果将n的坐标设置为0，也可以通过求最长路来使得1到n之间的距离最大。本题的约束条件有三个，ai-1 <= ai；ai - aj <= L；ai - aj >= D。暂且不去分析具体的约束条件，先讨论一个问题，什么情况下起点到终点的距离可以无限大。关于这个问题，很多博客仅仅给出了必要条件，比如说从起点到达不了终点，图中的两点间没有可达的路径，没有约束距离就无限大，但这仅仅是必要条件而非充分条件。比如下面的不等式组：a1 <= a2 - 1，a2 <= a3 - 1，最短路建图如下：

从a3是可以到达a1的，图中没有孤立的点，a3 = 0时，a1就可以无限小，他们的距离就无限大。这个简单的例子可以看出，差分约束的不等式组对应的图如果没有环，起点和终点的距离是可以无限大的。要想两点间距离有限，需要图中有一个适当的环，来约束解的范围。上图的不等式组可以推出a1 <= a3 - 2，那么我再加上一个不等式约束a1 >= a3 - 4,，就成功的将a1到a3之间的距离限制在4个单位以内了。对应图中的表现不过是a1到a3连一条边权为4的边，我们分析此时环的长度4 - 1 - 1 = 2是大于0的。所以我们可以得出下面的结论：最短路的图中如果存在负环，差分约束问题无合法解，如果存在正环，则正环上任意两点间的距离都是有限的，不存在环的图上任意两点间的距离都可以是无限大的。这个结论可以类比到最长路的图中。换一种表达形式的话就是如果要图中的两点间距离有限，只需要存在一个正环，且这两个点都在环上。那么本题我们是否需要判断了负环还要判断正环呢？实际上是不需要的。

第一个约束条件ai >= ai-1，构建的最短路图中an可以到达an-1,an-1可以到达an-2,...。所以an可以到达每一点，包括a1。我们先以an为起点，求一遍最短路，如果存在负环，则不等式组无解，如果不存在负环，那么不等式组肯定有解，下面要判断的就是an - a1的结果是否可以无限大。在确定了不等式组有解的情况下，我们以a1为起点再求一遍最短路，当然a1不一定能够到达每一点，如果a1到达不了an，说明不存在一个环，环上同时包含a1到an。如果a1出发可以到达an，则一定存在由a1、an构成的正环。从ai出发可以到达an，an出发可以到达a1，这个条件保证了环的存在。第一次以an为起点求最短路时不存在负环，说明这个环一定不是负环，那么就是正环了（即使环的长度为0也是有解的）。根据我们上一段推出的结论可知，此时a1和an之间的距离是有限的，并且第二次求最短路过程中a1是起点，求得的an是最大值，所以此时的an就是我们要求的最大距离了。

最后再总结下本题给我们的经验（仅仅是个人经验总结）。最短路存在负环，差分约束问题无解，最短路存在正环，环上任意两点之间距离有限，最短路不存在环，任意两点间距离可以是无穷大；最长路存在正环，差分约束问题无解，最长路存在负环，环上任意两点之间距离有限，最长路不存在环，任意两点间距离可以是无穷大。总的代码如下：

#include 
#include 
#include 
using namespace std;
const int N = 1005,M = 21005;
int idx,h[N],e[M],ne[M],w[M];
int n,cnt[N],d[N],q[N];
bool st[N];
void add(int a,int b,int c){
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
bool spfa(int s){
    memset(cnt,0,sizeof cnt);
    memset(st,false,sizeof st);
    memset(d,0x3f,sizeof d);
    d[s] = 0;
    q[0] = s;
    st[s] = true;
    int hh = 0,tt = 1;
    while(hh != tt){
        int u = q[hh++];
        st[u] = false;
        if(hh == N) hh = 0;
        for(int i = h[u];~i;i = ne[i]){
            int j = e[i];
            if(d[j] > d[u] + w[i]){
                d[j] = d[u] + w[i];
                cnt[j] = cnt[u] + 1;
                if(cnt[j] >= n) return false;;
                if(!st[j]){
                    st[j] = true;
                    q[tt++] = j;
                    if(tt == N) tt = 0;
                }
            }
        }
    }
    return true;
}
int main(){
    int ml,md,a,b,l;
    scanf("%d%d%d",&n,&ml,&md);
    memset(h,-1,sizeof h);
    for(int i = 2;i <= n;i++){
        add(i,i - 1,0);//最短路建图
    }
    while(ml--){
        scanf("%d%d%d",&a,&b,&l);
        if(a > b)   swap(a,b);
        add(a,b,l);
    }
    while(md--){
        scanf("%d%d%d",&a,&b,&l);
        if(a > b)   swap(a,b);
        add(b,a,-l);
    }
    if(!spfa(n))    puts("-1");//从n出发，存在负环，不等式无解
    else{
        spfa(1);
        if(d[n] == 0x3f3f3f3f)   puts("-2");//从1出发不能到达n，距离无限制
        else    printf("%d\n",d[n]);//存在正环，距离有限
    }
    return 0;
}