共轭梯度法
最速下降法
1.最速下降方向
函数f(x)在点x处沿方向d的变化率可用方向导数来表示。对于可微函数,方向导数等于梯度与方向的内积,即:
Df(x;d) = ▽f(x)Td,
因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下列非线性规划:
min ▽f(x)Td
s.t. ||d|| ≤ 1
当 d = -▽f(x) / ||▽f(x)||
时等号成立。因此,在点x处沿上式所定义的方向变化率最小,即负梯度方向为最速下降方向。
2.最速下降算法
最速下降法的迭代公式是
x(k+1) = x(k) + λkd(k) ,
其中d(k)是从x(k)出发的搜索方向,这里取在x(k)处的最速下降方向,即
d = -▽f(x(k)).
λk是从x(k)出发沿方向d(k)进行一维搜索的步长,即λk满足
f(x(k) + λkd(k)) = min f(x(k)+λd(k)) (λ≥0).
计算步骤如下:
(1)给定初点x(1) ∈ Rn,允许误差ε> 0, 置k = 1。
(2)计算搜索方向d = -▽f(x(k))。
(3)若||d(k)|| ≤ ε,则停止计算;否则,从x(k)出发,沿d(k)进行一维搜索,求λk,使
f(x(k) + λkd(k)) = min f(x(k)+λd(k)) (λ≥0).
(4)令x(k+1) = x(k) + λkd(k) ,置k = k + 1,转步骤(2)。
共轭梯度法
1.共轭方向
无约束问题最优化方法的核心问题是选择搜索方向。
以正定二次函数为例,来观察两个方向关于矩阵A共轭的几何意义。
设有二次函数:
f(x) = 1/2 (x - x*)TA(x - x*) ,
其中A是n×n对称正定矩阵,x*是一个定点,函数f(x)的等值面
1/2 (x - x*)TA(x - x*) = c
是以x*为中心的椭球面,由于
▽f(x*) = A(x - x*) = 0,
A正定,因此x*是f(x)的极小点。
设x(1)是在某个等值面上的一点,该等值面在点x(1)处的法向量
▽f(x(1)) = A(x(1) - x*)。
又设d(1)是这个等值面在d(1)处的一个切向量。记作
d(2) = x* - x(1)。
自然,d(1)与▽f(x(1))正交,即d(1)T▽f(x(1)) = 0,因此有
d(1)TAd(2) = 0,
即等值面上一点处的切向量与由这一点指向极小点的向量关于A共轭。
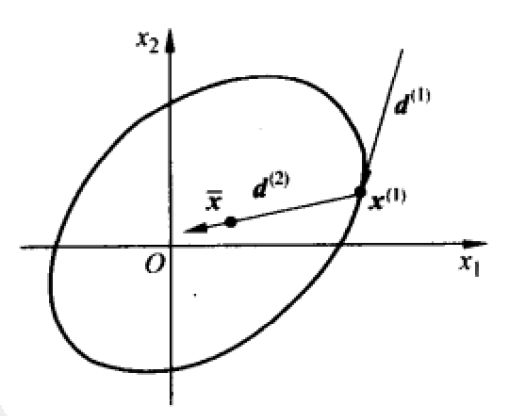
由此可知,极小化式所定义的二次函数,若依次沿着d(1)和d(2)进行一维搜索,则经两次迭代必达到极小点。
1.共轭梯度法
共轭梯度法最初由Hesteness和Stiefel于1952年为求解线性方程组而提出的。后来,人们把这种方法用于求解无约束最优化问题,使之成为一种重要的最优化方法。
Fletcher-Reeves共轭梯度法,简称FR法。
共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜素,求出目标函数的极小点。根据共轭方向基本性质,这种方法具有二次终止性。
对于二次凸函数的共轭梯度法:
min f(x) = 1/2 xTAx + bTx + c,
其中x∈ Rn,A是对称正定矩阵,c是常数。
具体求解方法如下:
首先,任意给定一个初始点x(1),计算出目标函数f(x)在这点的梯度,若||g1|| = 0,则停止计算;否则,令
d(1) = -▽f(x(1)) = -g1。
沿方向d(1)搜索,得到点x(2)。计算在x(2)处的梯度,若||g2|| ≠ 0,则利用-g2和d(1)构造第2个搜索方向d(2),在沿d(2)搜索。
一般地,若已知点x(k)和搜索方向d(k),则从x(k)出发,沿d(k)进行搜索,得到
x(k+1) = x(k) + λkd(k) ,
其中步长λk满足
f(x(k) + λkd(k)) = min f(x(k)+λd(k))。
此时可求出λk的显示表达

计算f(x)在x(k+1)处的梯度。若||gk+1|| = 0,则停止计算;否则,用-gk+1和d(k)构造下一个搜索方向d(k+1),并使d(k+1)和d(k)关于A共轭。按此设想,令
d(k+1) = -gk+1 + βkd(k),
上式两端左乘d(k)TA,并令
d(k)TAd(k+1) = -d(k)TAgk+1 + βkd(k)TAd(k) = 0,
由此得到
βk = d(k)TAgk+1 / d(k)TAd(k)。
再从x(k+1)出发,沿方向d(k+1)搜索。
在FR法中,初始搜索方向必须取最速下降方向,这一点决不可忽视。因子βk可以简化为:βk = ||gk+1||2 / ||gk||2。
3.非线性共轭梯度
当目标函数是高于二次的连续函数(即目标函数的梯度存在)时,其对应的解方程是非线性方程,非线性问题的目标函数可能存在局部极值,并且破坏了二次截止性,共轭梯度法需要在两个方面加以改进后,仍然可以用于实际的反演计算,但共轭梯度法不能确保收敛到全局极值。
(1)首先是共轭梯度法不能在n维空间内依靠n步搜索到达极值点,需要重启共轭梯度法,继续迭代,以完成搜索极值点的工作。
(2)在目标函数复杂,在计算时,由于需要局部线性化,需计算Hessian矩阵A,且计算工作量比较大,矩阵A也有可能是病态的。Fletcher和Reeves的方案最为常用,抛弃了矩阵A的计算,具体形式如下:

式中gk-1和gk分别为第k-1和第k次搜索是计算出来的目标函数的梯度。