伸展树
伸展树是一种相对简单的树结构,它保证从空树开始任意M次对树的操作最多花费O(MlogN)的时间。
这种保证并不能排除某次操作的时间为O(N)的可能,但是能保证每次操作平均的时间为O(logN)。对于一系列的操作,有的可能花费时间多些,有的少些。
伸展树基于这样的一个事实:
“对于时间花费为O(N}的二叉树操作是可以接受的,只要这种操作相对比较不频繁发生。”
对于一个二叉查找树,可能有的操作的时间为O(N),但是只要任意连续的M次操作的时间花费为O(MlogN),那么这种情况就是好的。
如果任意的一个操作可能有最坏的时间界(O(N)),那么如果我们仍要保持O(logN)的摊派时间的话,那么我们必须要移动访问过的结点。因为据经验,访问过的结点会有很大的可能被再次访问。因此如果访问了一个比较深的结点后,如果不移动它的话,那么结下来若干次的访问这个深结点,将会花掉大量的时间。
伸展树的basic idea:
“只要一个节点被访问过,那么就用AVL树的旋转方法把这个节点移动到根节点。”
如果一个节点比较深的话,那么会把很多相对较深的点一起移动到比较浅的位置。
伸展树不需要注意平衡信息以及高度问题,这是与AVL树不同的。
展开:
思想:沿着访问路径自底向上对节点进行旋转。若X(non-root)为访问的结点,
(1)如果X的父节点是root,那么我们只旋转root和X
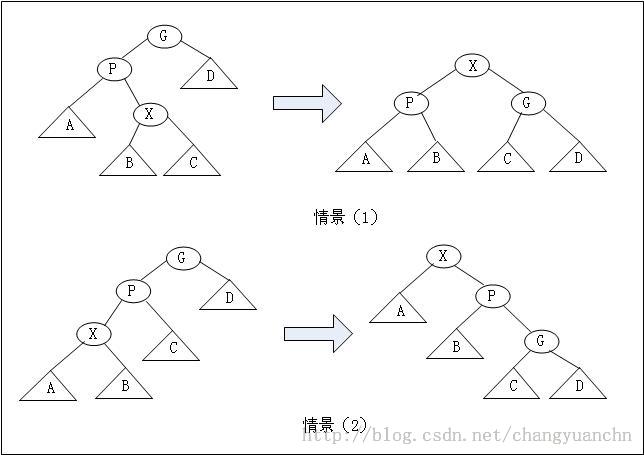
(2)否则的话,另X的父节点为X,祖父为G,那么就有2种情况需要考虑(如果算上对称的话,就是有4种情况)。
如果X是右节点,P是左节点,那么要做双旋转
如果X是左节点,P是左节点,那么要做单旋转
需要注意的是:AVL树的目的是平衡,而SPLAY树的目的是把访问节点移动到根节点,不需要考虑平衡的问题。
展开操作不仅可以将访问的结点移动到root,而且可以减小树的深度(大约每次以一半的效率),这个在小样本中不太明显,当节点比较多时,比较容易看到,如下图所示。因此展开树也是一个很神奇的东西。