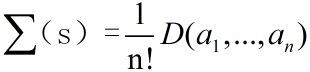线性代数(十八) : 行列式的几何意义

通过几何的视角理解行列式会更加清晰,理解行列式的性质也更容易。

1 有序单纯形

定义：R^n中的有序单纯形是一个具有n+1个顶点的多面体取其中一个顶点为原点并将其余点记做a1,...,an，则称0，a1,...,an为一个有序单纯形的顶点。

(i)顶点的顺序很重要。如：0，a1，a2，a3和0,a1,a3,a2是两个不同的单纯形

(ii)如果一个单纯形位于某个n-1维的空间上，则称之为退化的单纯形。

(iii)下边是一个三维空间下的单纯形(一个四面体)：

2 单纯形的定向性

对于一个非退化有序单形s=(0,a1,...,an)只可能有两种定向：正或者负，如果S可以连续并且非退化的变为标准有序单形(0,e1,...,en) 其中ej是标准基中的第j个向量

这个连续并且非退化的变化可以简单的理解为将单形做旋转伸缩等变化 但是保留顶点的相对位置,并且在变化的任意时刻单形都是非退化的。

(i)比如三维空间中的一个单形s=(0,e2,e1,e3) 就不能线序非退化的变为(0,e1,e2,e3)，因为在变化的过程中会有一刻s的前两个顶点会重合，这样s就变为退化的单形了。

(ii)从数论的角度出发如果顶点序列做奇置换为负,偶置换单形为正向。

3 单纯形体积与行列式

(i)对于非退化的有序单形S ，正向和负向时分别定义O(S)为+1和-1，当S为退化的单形的时候定义O(S)为零，下边给出单形体积的公式：

其中基表示S的一个n-1维的面

(ii)矩阵的行列式和有序单形的带符号体积有下边的关系D表示以a1,...,an为列的行列式。

(iii)可以根据该体积的几何性质推断出行列式的性质,从而确定行列式.