hdu 4888 2014多校第三场1002 Redraw Beautiful Drawings 网络流
思路:一开始以为是高斯消元什么的,想让队友搞,结果队友说不好搞,可能是网络流,我恍然,思路立马就有了。
我们建一个二部图,左边是行,右边是列,建个源点与行建边,容量是该行的和,列与新建的汇点建边,容量是该列的和,最后每行与每列建边,容量为题意中的k。建边如图:
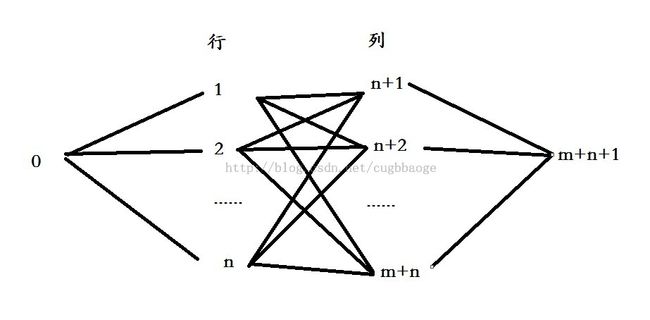
跑一遍最大流,如果最大流等于行的和且等于列的和,那么就是有解的,否则无解。这样我们得到了一组解,行i到列j的流量即为i行j列的大小。之后便是判断是否有多种情况了。基本思路是这样的,我们看下图:
有多解的情况一定可以找到这样的4个位置:AB同行,CD同行,AC同列,BD同列,并且他们符合一下两种情况的其中一种:
1、AD未达到k(可变大),BC不是0(可减小)
2、AD不是0(可减小),BC未达到k(可变大)
我们建一个二部图,左边是行,右边是列,建个源点与行建边,容量是该行的和,列与新建的汇点建边,容量是该列的和,最后每行与每列建边,容量为题意中的k。建边如图:

跑一遍最大流,如果最大流等于行的和且等于列的和,那么就是有解的,否则无解。这样我们得到了一组解,行i到列j的流量即为i行j列的大小。之后便是判断是否有多种情况了。基本思路是这样的,我们看下图:
有多解的情况一定可以找到这样的4个位置:AB同行,CD同行,AC同列,BD同列,并且他们符合一下两种情况的其中一种:
1、AD未达到k(可变大),BC不是0(可减小)
2、AD不是0(可减小),BC未达到k(可变大)
不过枚举的话复杂度太高了,这里需要优化下。我建了一个二维数组cc[i][j],代表之前行是否有第i个可变大,第j个可减小的情况。这里枚举每一行,每一行再枚举两个位置i和j,如果当前行有i和j使得第i可以减小、第j个可以变大并且cc[i][j]为1,那么一定有多解。这里如果cc[i][j]为0,那么继续,同时cc[j][i]赋为1。这样的话就避免了最坏O(400^4)的复杂度,而变成了最多O(400^3)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<cmath>
#define maxn 1<<29
using namespace std;
struct edge
{
int from,to,cap,flow;
};
vector<int>g[888];
vector<edge>edges;
int m,n,ma;
bool vis[888];
int d[888];
int cur[888];
int fl[444][444];
bool cc[444][444];
void init()
{
edges.clear();
int mm=m+n+1;
for(int i=0;i<=mm;i++)g[i].clear();
}
void add(int u,int v,int c)
{
edges.push_back((edge){u,v,c,0});
g[u].push_back(edges.size()-1);
edges.push_back((edge){v,u,0,0});
g[v].push_back(edges.size()-1);
}
bool bfs(int s,int t)
{
memset(vis,0,sizeof(vis));
queue<int>q;
q.push(s);
d[s]=0;
vis[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
int size=g[u].size();
for(int i=0;i<size;i++)
{
edge &e=edges[g[u][i]];
if(!vis[e.to]&&e.cap>e.flow)
{
vis[e.to]=1;
d[e.to]=d[u]+1;
q.push(e.to);
}
}
}
return vis[t];
}
int dfs(int u,int t,int mi)
{
if(u==t||mi==0)return mi;
int flow=0,f;
int size=g[u].size();
for(int &i=cur[u];i<size;i++)
{
edge &e=edges[g[u][i]];
if(d[u]+1==d[e.to]&&(f=dfs(e.to,t,min(mi,e.cap-e.flow)))>0)
{
e.flow+=f;
edges[g[u][i]^1].flow-=f;
flow+=f;
mi-=f;
if(mi==0)break;
}
}
return flow;
}
int dinic(int s,int t)
{
int flow=0;
while(bfs(s,t))
{
memset(cur,0,sizeof(cur));
flow+=dfs(s,t,maxn);
}
return flow;
}
bool go()
{
for(int i=1;i<=n;i++)
{
int size=g[i].size();
for(int j=0;j<size;j++)
{
edge &e=edges[g[i][j]];
if(e.to>n&&e.to<=m+n)
{
//cout<<e.from<<" "<<e.to<<" "<<e.flow<<endl;
fl[i][e.to-n]=e.flow;
}
}
}
memset(cc,0,sizeof(cc));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
for(int k=j+1;k<=m;k++)
{
bool v1=0,v2=0;
if(fl[i][j]!=ma&&fl[i][k]!=0)
{
if(cc[k][j])return true;
v1=1;
}
if(fl[i][j]!=0&&fl[i][k]!=ma)
{
if(cc[j][k])return true;
v2=1;
}
if(v1)cc[j][k]=1;
if(v2)cc[k][j]=1;
}
}
}
return false;
}
int main()
{
int u,v,c;
int s1,s2;
while(scanf("%d%d%d",&n,&m,&ma)!=EOF)
{
init();
s1=s2=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&c);
add(0,i,c);
s1+=c;
for(int j=1;j<=m;j++)
{
add(i,n+j,ma);
}
}
for(int i=1;i<=m;i++)
{
scanf("%d",&c);
add(n+i,m+n+1,c);
s2+=c;
}
int ans=dinic(0,m+n+1);
if(ans!=s1||ans!=s2)printf("Impossible\n");
else if(go())printf("Not Unique\n");
else
{
printf("Unique\n");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
printf("%d",fl[i][j]);
if(j==m)printf("\n");
else printf(" ");
}
}
}
}
return 0;
}