RBM

Restricted Boltzmann Machine - Short Tutorial

I have read a lot of papers on RBM and it seems to be difficult to grasp all the implementation details.
So, I want to share my experience with people facing the same problems. My tutorial is based on variant of RBM-s named Continuous Restricted Boltzmann Machine or CRBM for short. CRBM have very close implementation to original RBM with binomial neurons (0,1) as possible values of activation. At the end of the article I provide some code in Python. No guarantee is given that this implementation is correct so let me know of any bugs found.
First you may have a look at the original papers that describe theory behind RBM neural networks:

RBM application to Netflix challenge

Boltzmann Machine - Scholarpedia

Continuous RBM

WHAT IS A RESTRICTED BOLTZMANN MACHINE

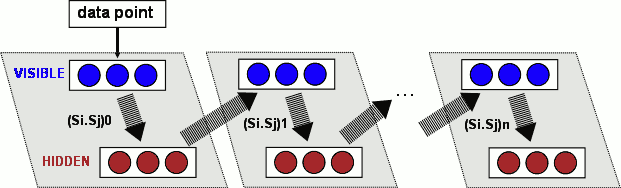
Restricted Boltzmann Machine is a stochastic neural network (that is a network of neurons where each neuron have some random behavior when activated). It consist of one layer of visible units (neurons) and one layer of hidden units. Units in each layer have no connections between them and are connected to all other units in other layer (fig.1). Connections between neurons are bidirectional and symmetric . This means that information flows in both directions during the training and during the usage of the network and that weights are the same in both directions.

fig.1 Restricted Boltzmann Machine

RBM Network works in the following way:
First the network is trained by using some data set and setting the neurons on visible layer to match data points in this data set.
After the network is trained we can use it on new unknown data to make classification of the data (this is known as unsupervised learning)

DATA SET

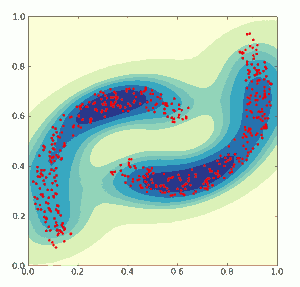
For purpose of this tutorial I will use artificially generated data set. It is 2D data that form a pattern shown in fig.2. I choose to use 500 data points for training. Because each data points is formed by to numbers between 0 and 1 neurons have to accept continuous values and I use Continuous RBM. I have tried different 2D patterns and this one seems to be relative difficult to be learned by CRBM.

fig. 2 Training data

LEARNING ALGORITHM

Training a RBM is performed by algorithm known as "Contrastive Divergence Learning".

More info on Contrastive Divergence 
Let W be the matrix of IxJ (I - number of visible neurons, J - number of hidden neurons) that represents
weights between neurons. Each neuron input is provided by connections from all neurons in other layer.
Current neuron state S is formed by multiplication of each input by weight, summation over all inputs and application of this sum as a argument of nonlinear sigmoidal function:
Sj = F( Sum( Si x Wij + N(0,sigma)) ) - here Si are all neurons in given layer plus one bias neuron that stays constantly set at 1.0
N(0,1) is random number from normal distribution with mean 0.0 and standard deviation sigma (I use sigma=0.2).
This nonlinear function in my case is:
F = lo + (hi - lo)/(1.0 + exp(-A*Sj))

Where lo and hi are the lower and higher bound of input values (in my case 0,1), so it
becomes: F = 1.0/(1.0 + exp(-A*Sj))
A - is some parameter that is determined during the learning process.

Contrastive divergence is a value that is computed (actually matrix of values) and that is used to adjust values of W matrix. Changing W incrementally lead to training of W values.

Let W0 be the initial matrix of weights that are set to some random small values. I use N(0, 0.1) for this.
Let CD = <Si.Sj>0 - <Si.Sj>n  - contrastive divergence
Then on each step (epoch) W is updated to new value W".:
W" = W + alpha*CD
Here alpha is some small step - "learning rate". There exist more complex ways for W update that involve
some "momentum" and "cost" of update to avoid W values to become very large.

CONTRASTIVE DIVERGENCE EXPLANATION

There seems to be big confusion what exactly Contrastive Divergence means and how to implement it.
I have spend a lot of time to understand it.
First of all CD as shown in the formula above is a matrix of size IxJ. So this formula have to be
computed for each combination of I and J.
<...> is a average over each data point in the data set.

Si.Sj is just a multiplication of current activation (state) of neuron I and neuron J (obviously :) ). Where Si is the state of a visible neuron, and Sj is the state of a hidden neuron.
Indexes after <...> mean that average is taken after 0 or N-th reconstruction step performed.

fig. 2 Training Restricted Boltzmann Machine

How is the reconstruction performed?

1. get one data point from data set.
2. use values of this data point to set state of visible neurons Si
3. compute Sj for each hidden neuron based on formula above and states of visible neurons Si
4. now Si and Sj values can be used to compute (Si.Sj)0 - here (...) means just values not average
5. on visible neurons compute Si using the Sj computed in step3. This is known as ".reconstruction"
6. compute state of hidden neurons Sj again using Si from 5 step.
7. now use Si and Sj to compute (Si.Sj)1 (fig.3)
8. repeating multiple times steps 5,6 and 7 compute (Si.Sj)n. Where n is small number and can increase with learning steps to achieve better accuracy.

The algorithm as a whole is:

• For each epoch do:
  • For each data point in data set do:
    • CDpos =0, CDneg=0 (matrices)
    • perform steps 1...8
    • accumulate CDpos = CDpos + (Si.Sj)0
    • accumulate CDneg = CDneg + (Si.Sj)n
  • At the end compute average of CDpos and CDneg by dividing them by number of data points.
  • Compute CD = < Si.Sj >0 - < Si.Sj >n = CDpos - CDneg
  • Update weights and biases W" = W + alpha*CD (biases are just weights to neurons that stay always 1.0)
  • Compute some "error function" like sum of squared difference between Si in 1) and Si in 5)
    e.g between data and reconstruction.
• repeat for the next epoch until error is small or some fixed number of epoch.

The value of parameter A for visible units stay constant and for hidden unit is adjusted
by the same CD calculation but instead of formula above the following formula is used:
CD = (<Sj.Sj>0 - <Sj.Sj>n)/(Aj.Aj)

In my code i use n=20 initially and gradually increase it to 50.
Most of the steps in the algorithm can be performed by some simple matrix multiplication.

RBM USAGE

After the RBM learning process finishes it can be shown how well it performs on new data points.
I use set of 500 data points that are random and uniformly distributed in the 2D interval (0..1, 0..1).
Visible layer neurons states are set with values of each data point and steps 1) 2) 3) 5) are repeated
multiple times. Number of repetitions is the max number of "n". used in the learning process.

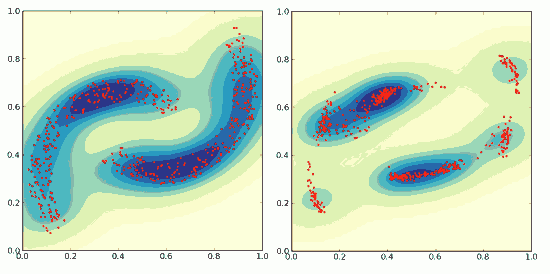
At the end of n-th step, neurons states in visible layer represent a data reconstruction. This is repeated for each data point. All the reconstruction points form a 2D image pattern that can be compared with initial image.

PYTHON IMPLEMENTATION OF CRBM

At the end of this article I provide some implementation of Continuous Restricted Boltzmann Machine in Python. Most of the steps are performed by matrix operations using NumPy library. I used PyLab and SciPy to make some nice visualizations. Images of data that are shown (fig.4) are interpolated with Gaussian kernel in order to have some "feeling" of the density of data points and reconstructed data points.

fig. 4 Training data and reconstruction.

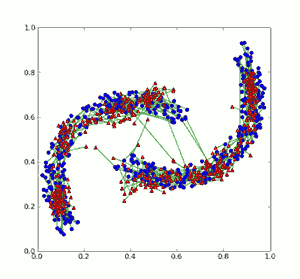
Next image shows initial data set and reconstructed data superimposed. Initial data is in blue, reconstructed in red and green line connects each data point with reconstructed one.

Fig. 5 Training data (blue) and reconstruction (red) superimposed.

Main difficulty I observed is to fine tune the set of learning parameters.

I used the following parameters and if somebody is able to find better values - let me know.
sigma=0.2
A=0.1 (on visible neurons)
Learning Rate W = 0.5
Learning Rate A = 0.5
Learning Cost = 0.00001
Learning Moment = 0.9

RBM architecture is 2 visible neurons for 2D data points and 8 hidden neurons. On some experiments with simple patterns 4 neurons are enough to reconstruct pattern successfully.

Boltzmann machine

Geoffrey E. Hinton (2007), Scholarpedia, 2(5):1668.

doi:10.4249/scholarpedia.1668

revision #91075 [link to/cite this article]

Curator and Contributors

1.00 - Geoffrey E. Hinton

• Dr. Geoffrey E. Hinton, University of Toronto, CANADA

A Boltzmann machine is a network of symmetrically connected, neuron-like units that make stochastic decisions about whether to be on or off. Boltzmann machines have a simple learning algorithm (Hinton & Sejnowski, 1983) that allows them to discover interesting features that represent complex regularities in the training data. The learning algorithm is very slow in networks with many layers of feature detectors, but it is fast in "restricted Boltzmann machines" that have a single layer of feature detectors. Many hidden layers can be learned efficiently by composing restricted Boltzmann machines, using the feature activations of one as the training data for the next.

Boltzmann machines are used to solve two quite different computational problems. For a search problem, the weights on the connections are fixed and are used to represent a cost function. The stochastic dynamics of a Boltzmann machine then allow it to sample binary state vectors that have low values of the cost function.

For a learning problem, the Boltzmann machine is shown a set of binary data vectors and it must learn to generate these vectors with high probability. To do this, it must find weights on the connections so that, relative to other possible binary vectors, the data vectors have low values of the cost function. To solve a learning problem, Boltzmann machines make many small updates to their weights, and each update requires them to solve many different search problems.

The stochastic dynamics of a Boltzmann machine

When unit  i  is given the opportunity to update its binary state, it first computes its total input,  zi ,  which is the sum of its own bias,  bi ,  and the weights on connections coming from other active units:

zi=bi+∑jsjwij(1)

where  wij  is the weight on the connection between  i  and  j ,  and  sj  is  1  if unit  j  is on and  0  otherwise. Unit  i  then turns on with a probability given by the logistic function:

prob(si=1)  =  11+e−zi(2)

If the units are updated sequentially in any order that does not depend on their total inputs, the network will eventually reach a Boltzmann distribution (also called its equilibrium or stationary distribution) in which the probability of a state vector,  v ,  is determined solely by the "energy" of that state vector relative to the energies of all possible binary state vectors:

P(v)=e−E(v)/∑ue−E(u)(3)

As in Hopfield nets, the energy of state vector  v  is defined as

E(v)=−∑isvibi−∑i<jsvisvjwij(4)

where  svi  is the binary state assigned to unit  i  by state vector  v .

If the weights on the connections are chosen so that the energies of state vectors represent the cost of those state vectors, then the stochastic dynamics of a Boltzmann machine can be viewed as a way of escaping from poor local optima while searching for low-cost solutions. The total input to unit  i ,   zi ,  represents the difference in energy depending on whether that unit is off or on, and the fact that unit  i  occasionally turns on even if  zi  is negative means that the energy can occasionally increase during the search, thus allowing the search to jump over energy barriers.

The search can be improved by using simulated annealing. This scales down all of the weights and energies by a factor,  T ,  which is analogous to the temperature of a physical system. By reducing T from a large initial value to a small final value, it is possible to benefit from the fast equilibration at high temperatures and still have a final equilibrium distribution that makes low-cost solutions much more probable than high-cost ones. At a temperature of  0  the update rule becomes deterministic and a Boltzmann machine turns into a Hopfield Network

Learning in Boltzmann machines

Learning without hidden units

Given a training set of state vectors (the data), learning consists of finding weights and biases (the parameters) that make those state vectors good. More specifically, the aim is to find weights and biases that define a Boltzmann distribution in which the training vectors have high probability. By differentiating Eq. (3) and using the fact that  ∂E(v)/∂wij=−svisvj  it can be shown that

⟨∂logP(v)∂wij⟩data=⟨sisj⟩data−⟨sisj⟩model(5)

where  ⟨⋅⟩data  is an expected value in the data distribution and  ⟨⋅⟩model  is an expected value when the Boltzmann machine is sampling state vectors from its equilibrium distribution at a temperature of 1. To perform gradient ascent in the log probability that the Boltzmann machine would generate the observed data when sampling from its equilibrium distribution,  wij  is incremented by a small learning rate times the RHS of Eq. (5). The learning rule for the bias,  bi ,  is the same as Eq. (5), but with  sj  ommitted.

If the observed data specifies a binary state for every unit in the Boltzmann machine, the learning problem is convex: There are no non-global optima in the parameter space. However, sampling from  ⟨⋅⟩model  may involve overcoming energy barriers in the binary state space.

Learning with hidden units

Learning becomes much more interesting if the Boltzmann machine consists of some "visible" units, whose states can be observed, and some "hidden" units whose states are not specified by the observed data. The hidden units act as latent variables (features) that allow the Boltzmann machine to model distributions over visible state vectors that cannot be modelled by direct pairwise interactions between the visible units. A surprising property of Boltzmann machines is that, even with hidden units, the learning rule remains unchanged. This makes it possible to learn binary features that capture higher-order structure in the data. With hidden units, the expectation  ⟨sisj⟩data  is the average, over all data vectors, of the expected value of  sisj  when a data vector is clamped on the visible units and the hidden units are repeatedly updated until they reach equilibrium with the clamped data vector.

It is surprising that the learning rule is so simple because  ∂logP(v)/∂wij  depends on all the other weights in the network. Fortunately, the locally available difference in the two correlations in Eq. (5) tells  wij  everthing it needs to know about the other weights. This makes it unnecessary to explicitly propagate error derivatives, as in the backpropagation algorithm.

Different types of Boltzmann machine

Higher-order Boltzmann machines

The stochastic dynamics and the learning rule can accommodate more complicated energy functions (Sejnowski, 1986). For example, the quadratic energy function in Eq. (4) can be replaced by an energy function whose typical term is  sisjskwijk .  The total input to unit  i  that is used in the update rule must then be replaced by  zi=bi+∑j<ksjskwijk .  The only change in the learning rule is that  sisj  is replaced by  sisjsk .

Conditional Boltzmann machines

Boltzmann machines model the distribution of the data vectors, but there is a simple extension for modeling conditional distributions (Ackley et. al. ,1985). The only difference between the visible and the hidden units is that, when sampling  ⟨sisj⟩data ,  the visible units are clamped and the hidden units are not. If a subset of the visible units are also clamped when sampling  ⟨sisj⟩model  this subset acts as "input" units and the remaining visible units act as "output" units. The same learning rule applies, but now it maximizes the log probabilities of the observed output vectors conditional on the input vectors.

Mean field Boltzmann machines

Instead of using units that have stochastic binary states, it is possible to use "mean field" units that have deterministic, real-valued states between 0 and 1, as in an analog Hopfield net. Eq. (2) is used to compute an "ideal" value for a unit's state given the current states of the other units and the actual value is moved towards the ideal value by some fraction of the difference. If this fraction is small, all the units can be updated in parallel. The same learning rules can be used by simply replacing the stochastic, binary values by the deterministic real-values (Petersen and Andersen, 1987), but the learning algorithm is hard to justify and mean field nets have problems modeling multi-modal distributions.

Non-binary units

The binary stochastic units used in Boltzmann machines can be generalized to "softmax" units that have more than 2 discrete values, Gaussian units whose output is simply their total input plus Gaussian noise, binomial units, Poisson units, and any other type of unit that falls in the exponential family (Welling et. al., 2005). This family is characterized by the fact that the adjustable parameters have linear effects on the log probabilities. The general form of the gradient required for learning is simply the change in the sufficient statistics caused by clamping data on the visible units.

The speed of learning

Learning is typically very slow in Boltzmann machines with many hidden layers because large networks can take a long time to approach their equilibrium distribution, especially when the weights are large and the equilibrium distribution is highly multimodal, as it usually is when the visible units are unclamped. Even if samples from the equilibrium distribution can be obtained, the learning signal is very noisy because it is the difference of two sampled expectations. These difficulties can be overcome by restricting the connectivity, simplifying the learning algorithm, and learning one hidden layer at a time.

Restricted Boltzmann machines

A restricted Boltzmann machine (Smolensky, 1986) consists of a layer of visible units and a layer of hidden units with no visible-visible or hidden-hidden connections. With these restrictions, the hidden units are conditionally independent given a visible vector, so unbiased samples from  ⟨sisj⟩data  can be obtained in one parallel step. To sample from  ⟨sisj⟩model  still requires multiple iterations that alternate between updating all the hidden units in parallel and updating all of the visible units in parallel. However, learning still works well if  ⟨sisj⟩model  is replaced by  ⟨sisj⟩reconstruction  which is obtained as follows:

1. Starting with a data vector on the visible units, update all of the hidden units in parallel.
2. Update all of the visible units in parallel to get a "reconstruction".
3. Update all of the hidden units again.

This efficient learning procedure does approximate gradient descent in a quantity called "contrastive divergence" and works well in practice (Hinton, 2002).

Learning deep networks by composing restricted Boltzmann machines

After learning one hidden layer, the activity vectors of the hidden units, when they are being driven by the real data, can be treated as "data" for training another restricted Boltzmann machine. This can be repeated to learn as many hidden layers as desired. After learning multiple hidden layers in this way, the whole network can be viewed as a single, multilayer generative model and each additional hidden layer improves a lower bound on the probability that the multilayer model would generate the training data (Hinton et. al., 2006).

Learning one hidden layer at a time is a very effective way to learn deep neural networks with many hidden layers and millions of weights. Even though the learning is unsupervised, the highest level features are typically much more useful for classification than the raw data vectors. These deep networks can be fine-tuned to be better at classification or dimensionality reduction using the backpropagation algorithm (Hinton & Salakhutdinov, 2006). Alternatively, they can be fine-tuned to be better generative models using a version of the "wake-sleep" algorithm (Hinton et. al., 2006).

Relationships to other models

Markov random fields and Ising models

Boltzmann machines are a type of Markov random field, but most Markov random fields have simple, local interaction weights which are designed by hand rather than being learned. Boltzmann machines are Ising models, but Ising models typically use random or hand-designed interaction weights.

Graphical models

The learning algorithm for Boltzmann machines was the first learning algorithm for undirected graphical models with hidden variables (Jordan 1998). When restricted Boltzmann machines are composed to learn a deep network, the top two layers of the resulting graphical model form an unrestricted Boltzmann machine, but the lower layers form a directed acyclic graph with directed connections from higher layers to lower layers (Hinton et. al. 2006).

Gibbs sampling

The search procedure for Boltzmann machines is an early example of Gibbs sampling, a Markov chain Monte Carlo method which was invented independently (Geman & Geman, 1984) and was also inspired by simulated annealing.

Conditional random fields

Conditional random fields (Lafferty et. al., 2001) can be viewed as simplified versions of higher-order, conditional Boltzmann machines in which the hidden units have been eliminated. This makes the learning problem convex, but removes the ability to learn new features.

References

• Ackley, D., Hinton, G., and Sejnowski, T. (1985). A Learning Algorithm for Boltzmann Machines. Cognitive Science, 9(1):147-169.

• Geman, S. and Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 6(6):721-741.

• Hinton, G. E. (2002). Training products of experts by minimizing contrastive divergence. Neural Computation, 14(8):1711-1800.

• Hinton, G. E, Osindero, S., and Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neural Computation, 18:1527-1554.

• Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313:504-507.

• Hinton, G. E. and Sejnowski, T. J. (1983). Optimal Perceptual Inference. Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Washington DC, pp. 448-453.

• Jordan, M. I. (1998) Learning in Graphical Models, MIT press, Cambridge Mass.

• Lafferty, J. and McCallum, A. and Pereira, F. (2001) Conditional random fields: Probabilistic models for segmenting and labeling sequence data. Proc. 18th International Conf. on Machine Learning, pages 282-289 Morgan Kaufmann, San Francisco, CA

• Peterson, C. and Anderson, J.R. (1987), A mean field theory learning algorithm for neural networks. Complex Systems, 1(5):995--1019.

• Sejnowski, T. J. (1986). Higher-order Boltzmann machines. AIP Conference Proceedings, 151(1):398-403.

• Smolensky, P. (1986). Information processing in dynamical systems: Foundations of harmony theory. In Rumelhart, D. E. and McClelland, J. L., editors, Parallel Distributed Processing: Volume 1: Foundations, pages 194-281. MIT Press, Cambridge, MA.

• Welling, M., Rosen-Zvi, M., and Hinton, G. E. (2005). Exponential family harmoniums with an application to information retrieval. Advances in Neural Information Processing Systems 17, pages 1481-1488. MIT Press, Cambridge, MA.

Internal references

• James Meiss (2007) Dynamical systems. Scholarpedia, 2(2):1629.
• Eugene M. Izhikevich (2007) Equilibrium. Scholarpedia, 2(10):2014.
• John J. Hopfield (2007) Hopfield network. Scholarpedia, 2(5):1977.

See also

Associative Memory, Boltzmann Distribution, Hopfield Network, Neural Networks, Simulated Annealing, Unsupervised Learning

Sponsored by: Eugene M. Izhikevich, Editor-in-Chief of Scholarpedia, the peer-reviewed open-access encyclopedia

Reviewed by: Anonymous

Reviewed by: Dr. Zoubin Ghahramani, Department of Engineering, University of Cambridge, UK, and Carnegie Mellon Univerisity, USA

Reviewed by: Dr. Barak Pearlmutter, Hamilton Institute, National University of Ireland Maynooth, Co. Kildare, Ireland

Accepted on: 2007-05-24 18:16:00 GMT

Categories: 

• Recurrent Neural Networks
• Computational Intelligence
• Computational Neuroscience