hdu 4862 费用流

官方题解：

最小K路径覆盖的模型，用费用流或者KM算法解决，构造二部图，X部有N*M个节点，源点向X部每个节点连一条边，流量1，费用0，Y部有N*M个节点，每个节点向汇点连一条边，流量1，费用0，如果X部的节点x可以在一步之内到达Y部的节点y，那么就连边x->y，费用为从x格子到y格子的花费能量减去得到的能量，流量1，再在X部增加一个新的节点，表示可以从任意节点出发K次，源点向其连边，费用0，流量K，这个点向Y部每个点连边，费用0，流量1，最这个图跑最小费用最大流，如果满流就是存在解，反之不存在，最小费用的相反数就是可以获得的最大能量

个人理解：

昨儿在比赛时大致看了下这题，也想到了网络流，但是由于题意没理解清楚，并且个人太菜，没能想到正确的方法。

对于官方的题解，很简单的表述，但是要理解透却没那么容易（特别对于我这种菜鸟）。经过吃饭、走路时间的思考，终于略有感触，下面谈谈我的理解吧。

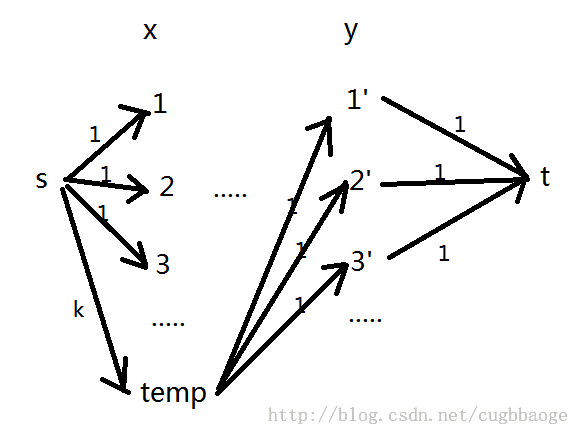
我画了这张图：

为什么建在x集再建一个点就好了呢？首先我们可以想想没有这个点的情况，那么y集一些点到t会有流量，这些点是作为跳的终点能到达的点，而y集到t没有流量的那些点就必须是作为起点到达了，所以在x集加一个点给它k的流量，如果这样能满留，就说明起点数量在k个以内，就符合条件了。

一开始，我想能不能不加这个点而是判断它的流量是不是达到了m*n-k，但后来观察前三组样例，实践+思考后，发现这个是不行的，想一想不难发现，费用流求解过程中是优先流量大，其次才是保证费用的最值，这里的满留在题中的含义就是能遍历全图，如果不加这个点，它也是优先流量大，因而会单纯为了流量大而取到较小的cost值，从而得到较小的错误答案。

理解了这个，相信离A题也不远了，之后就是费用流的方法即可。

为了改善自己的代码风格，我的代码参考白书（训练指南），希望自己以后不要因为恶劣的代码风格浪费大量debug时间了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<cmath>
#define INF 1000007
using namespace std;
struct edge
{
    int from,to,cap,flow,cost;
};
vector<edge>edges;
vector<int>g[300];
char grid[15][15];
int m,n,k;
bool inq[300];
int d[300];
int pre[300];
int a[300];
int maxflow;
void init()
{
    edges.clear();
    int num=2*m*n+2;
    for(int i=0;i<=num;i++)g[i].clear();
}
void add(int from,int to,int cap,int cost)
{
    edges.push_back((edge){from,to,cap,0,cost});
    g[from].push_back(edges.size()-1);
    edges.push_back((edge){to,from,0,0,-cost});
    g[to].push_back(edges.size()-1);
}
void build(int s,int t)
{
    int temp=2*m*n+2;
    int num=m*n;
    add(s,temp,k,0);
    for(int i=1;i<=num;i++)
    {
        add(s,i,1,0);
        add(num+i,t,1,0);
        add(temp,num+i,1,0);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            for(int k=i+1;k<=n;k++)
            {
                if(grid[i-1][j-1]==grid[k-1][j-1])add((i-1)*m+j,num+(k-1)*m+j,1,(grid[i-1][j-1]-'0')+i-k+1);
                else add((i-1)*m+j,num+(k-1)*m+j,1,i-k+1);
            }
            for(int k=j+1;k<=m;k++)
            {
                if(grid[i-1][j-1]==grid[i-1][k-1])add((i-1)*m+j,num+(i-1)*m+k,1,(grid[i-1][j-1]-'0')+j-k+1);
                else add((i-1)*m+j,num+(i-1)*m+k,1,j-k+1);
            }
        }
    }
}
bool BellmanFord(int s,int t,int &cost)
{
    int num=2*m*n+2;
    for(int i=0;i<=num;i++)d[i]=-INF;
    memset(inq,0,sizeof(inq));
    d[s]=0;inq[s]=1;pre[s]=-1;a[s]=INF;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        inq[u]=0;
        int size=g[u].size();
        for(int i=0;i<size;i++)
        {
            edge &e=edges[g[u][i]];
            if(e.cap>e.flow&&d[e.to]<d[u]+e.cost)
            {
                d[e.to]=d[u]+e.cost;
                pre[e.to]=g[u][i];
                a[e.to]=min(a[u],e.cap-e.flow);
                if(!inq[e.to])
                {
                    q.push(e.to);
                    inq[e.to]=1;
                }
            }
        }
    }
    if(d[t]==-INF)return false;
    maxflow+=a[t];
    cost+=d[t]*a[t];
    int u=t;
    while(u!=s)
    {
        edges[pre[u]].flow+=a[t];
        edges[pre[u]^1].flow-=a[t];
        u=edges[pre[u]].from;
    }
    return true;
}
int mincost(int s,int t)
{
    int cost=0;
    while(BellmanFord(s,t,cost));
    return cost;
}
void solve()
{
    init();
    int s=0;
    int t=2*m*n+1;
    build(s,t);
    getchar();
    maxflow=0;
    int ans=mincost(s,t);
    if(maxflow==m*n)cout<<ans<<endl;
    else cout<<-1<<endl;
}
int main()
{
    int ca=1;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&k);
        for(int i=0;i<n;i++)scanf("%s",grid[i]);
        printf("Case %d : ",ca++);
        solve();
    }
    return 0;
}