CF335E Counting Skyscrapers
题意:
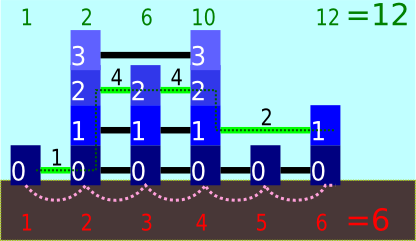
现有一排摩天大楼,每个大楼高度为i的概率为2 - i-1,且高度从0开始计算;
每两个能看见的相同高度的楼层之间都有滑索相连,权值为2^高度;
A的值为摩天大楼个数;
B的值从1开始累加,一个人从1出发,每次在这个楼最高的滑索向右滑,并在计数器上加这个滑索的权值;
而因为这个人有恐高症,所以他不会经过高度超过h的楼层;
已知A或者B的值n和高度限制h,求另一个计数器的期望值;
n<=30000,h<=30;
题解:
很神奇的概率DP题。。首先考虑怎么从A算出B;
因为每次他都是选择从最高的索道向前走,因此就有这么一种思路:从低到高枚举层数,每次计算新加入的一层对答案的贡献;
那么最底层的贡献就是n-1了,注意计数器从1开始计数;
设当前层数增加到了i,然后再枚举这个索道的长度j;
这个索道可能出现的地方有n-j个,每次出现的概率是:
(12i)2(1−12i)j−1
因为要两边的楼不低于i且中间的所有楼低于i;
然后考虑每一个这样的索道的得分,就是它本身的得分再减去被它覆盖的期望得分;
因为我们逐层搞的过程中已经消去了一些,所以只需要考虑i-1层期望有多少个索道就可以了;
索道数等于两个楼之间高度恰为i-1楼的个数+1,而一个楼为i-1层的概率为2^(-i);
但是在之前的讨论中已经确定它小于i层了 (否则那个索道不可能存在),所以它是i-1层的概率为:
12i1−12i=12i−1
之后再乘上j-1为期望楼数,再+1为期望索道数,再乘上2^(i-1)为得分,用2^i减去即为i层有一个长度为j索道的得分;
于是整个的公式为:
ans=nans+=∑hi=1∑n−1j−1(2i−2i−1((j−1)12i−1+1))⋅ (n−j)(12i)2(1−12i)j−1
时间复杂度显然为O(n*h)的,于是我们解决了第一问;
第二问输出n即可= =;
原因就是在第i层经过一个滑索,得分为2^i,而期望经过的大楼数也是2^i;
代码:
#include<math.h>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 31000
#define M 40
using namespace std;
char str[M];
double pow2[N],dpow2[N];
int main()
{
int n,m,i,j;
double ans;
scanf("%s%d%d",str,&n,&m);
if(str[0]=='B')
{
printf("%d\n",n);
return 0;
}
pow2[0]=dpow2[0]=1;
for(i=1;i<=m;i++)
pow2[i]=pow2[i-1]*2,dpow2[i]=1/pow2[i];
ans=n;
for(i=1;i<=m;i++)
{
for(j=1;j<n;j++)
{
ans+=(pow2[i]-pow2[i-1]*((j-1)/(pow2[i]-1)+1))*
(n-j)*dpow2[i]*dpow2[i]*pow((1-dpow2[i]),j-1);
}
}
printf("%.9lf\n",ans);
return 0;
}