多重背包

整理自背包问题九讲笔记_多重背包

1、问题描述

已知:有一个容量为V的背包和N件物品，第i件物品最多有Num[i]件，每件物品的重量是weight[i]，收益是cost[i]。

问题:在不超过背包容量的情况下，最多能获得多少价值或收益

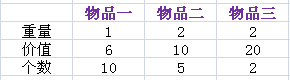
举例：物品个数N = 3，背包容量为V = 8，则背包可以装下的最大价值为64.

----------------------------------------------

2、转换为01背包问题求解（直接利用01背包）

思路 1、直接对每一件物品进行拆分成Num[i]件，之后在拆分后的集合上进行01背包的求解。

时间复杂度：O(V*Σ(Weight[i]))。太慢不好。

思路 2、采用二进制拆分的思想。对每i件物品，拆分的策略为：新拆分的物品的重量等于1件,2件,4件,..,(2^(k - 1)),Num[i] - (2^(k - 1))件，其中k 是满足Num[i] - 2^k + 1 > 0 的最大整数。

注意：

（1）最后一个物品的件数的求法和前面不同，其直接等于 该物品的最大件数 - 前面已经分配之和。

（2）分成的这几件物品的系数和为Num[i]，表明第i种物品取的件数不能多于Num[i]。

举例：某物品为13件，则其可以分成四件物品，其系数为1,2,4,6.这里k = 3。

当然，这里使用二进制的前提还是使用二进制拆分能保证对于0,,,Num[i]间的每一个整数，均可以用若干个系数的和表示。

具体使用时，有一个小优化，即：

我们不对所有的物品进行拆分，因此物品一旦拆分，其物品个数肯定增加，那么复杂度肯定上去。

此时，我们可以选择性地对物品进行拆分：

（1）如果第i个物品的重量Weight[i] * 物品的个数Num[i] >= 背包总重量V，可以不用拆分。

（2）如果第i个物品的重量Weight[i] * 物品的个数Num[i] < 背包总重量V，需要拆分。

其实，拆不拆分，就看该物品能不能满足完全背包的条件。即，看该物品能不能无限量供应。

解释：为啥满足Weight[i] * 物品的个数Num[i] >= 背包总重量V的物品可以不用拆分?

此时，满足该条件时，此物品相当于是无限供应，直到背包放不下为止。

最终，对于不需要拆分的物品，可以看成完全背包的情况，调用处理完全背包物品的函数；对于需要拆分的物品，可以看成01背包的情况，调用处理01背包物品的函数。

这样，由于不对满足完全背包的物品进行拆分，此时物品个数就没有对所有物品拆分时的物品个数多，即程序中外层循环降低，复杂度也就下去了。

伪代码：

这里：C表示该物品的重量。M表示该物品的个数。V表示背包的最大容量。W表示该物品的收益。

代码：

 #include <iostream>
 using namespace std;

 const int N = 3;//物品个数
 const int V = 8;//背包容量
 int Weight[N + 1] = {0,1,2,2};
 int Value[N + 1] = {0,6,10,20};
 int Num[N + 1] = {0,10,5,2};

 int f[V + 1] = {0};
 /*
 f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。
 f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
 v的为逆序
 */
 void ZeroOnePack(int nWeight,int nValue)
 {
     for (int v = V;v >= nWeight;v--)
     {
         f[v] = max(f[v],f[v - nWeight] + nValue);
     }
 }

 /*
 f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。
 f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
 v的为增序
 */
 void CompletePack(int nWeight,int nValue)
 {
     for (int v = nWeight;v <= V;v++)
     {
         f[v] = max(f[v],f[v - nWeight] + nValue);
     }
 }

 int MultiKnapsack()
 {
     int k = 1;
     int nCount = 0;
     for (int i = 1;i <= N;i++)
     {
         if (Weight[i] * Num[i] >= V)
         {
             //完全背包:该类物品原则上是无限供应，
             //此时满足条件Weight[i] * Num[i] >= V时，
             //表示无限量供应，直到背包放不下为止.
             CompletePack(Weight[i],Value[i]);
         }
         else
         {
             k = 1;
             nCount = Num[i];
             while(k <= nCount)
             {
                 ZeroOnePack(k * Weight[i],k * Value[i]);
                 nCount -= k;
                 k *= 2;
             }
             ZeroOnePack(nCount * Weight[i],nCount * Value[i]);
         }
     }
     return f[V];
 }

 int main()
 {
     cout<<MultiKnapsack()<<endl;
     system("pause");
     return 1;
 }