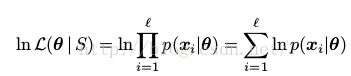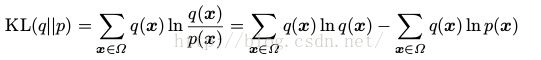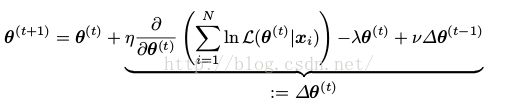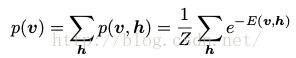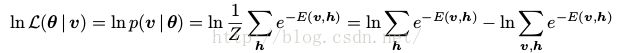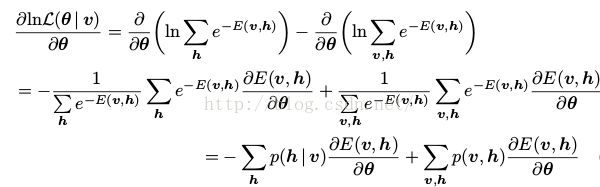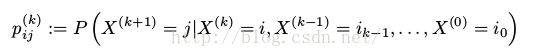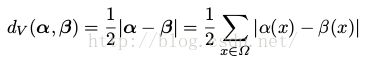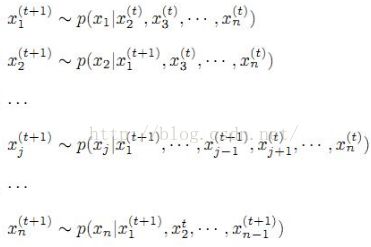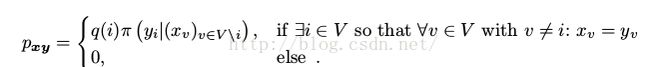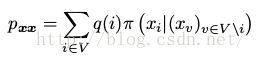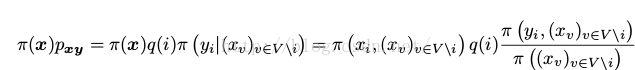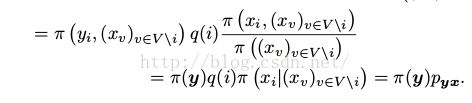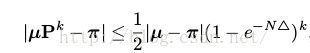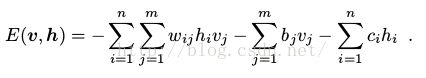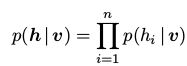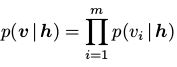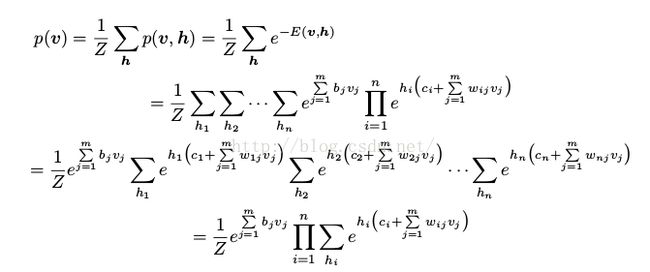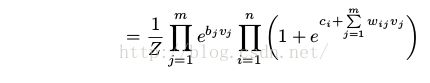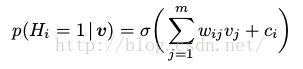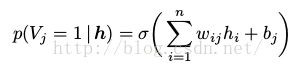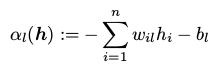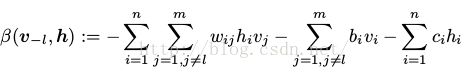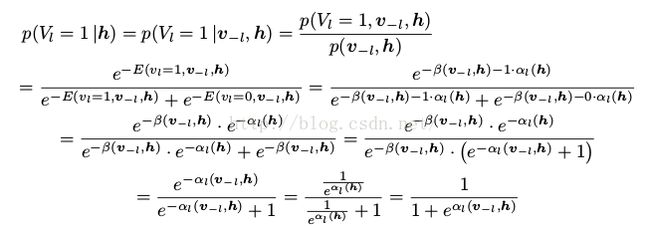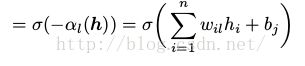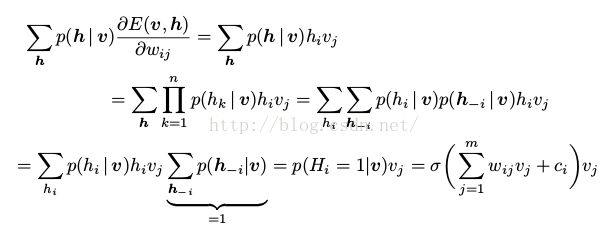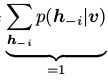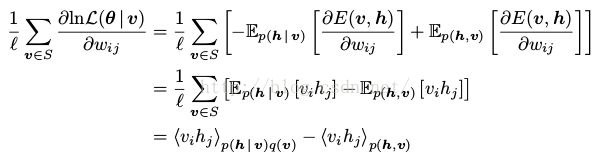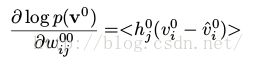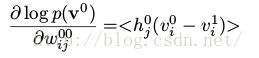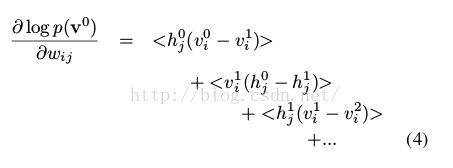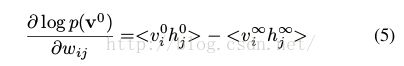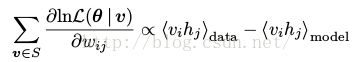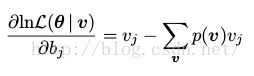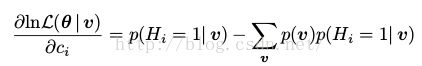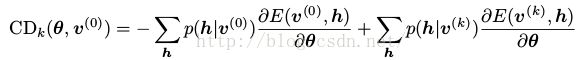翻译自 An Introduction to Restricted Boltzmann Machinesby Asja Fischer 1,2 and Christian Igel 2
2.2Unsupervised Learning
非监督学习意味着学习一个由样本学习出一个未知的分布q,这个过程包括了对原始数据找到的新的表示,来进行学习、规范化。假设我们已经知道图的结构并且能量函数属于一个已知的函数族f(θ),利用MRF的非监督学习过程就是不断的去调整参数θ。
考虑训练集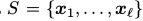 。假设数据样本是独立且唯一的。就是说,他们是相互独立被从q中采样出来的。我们一般用极大似然来估计参数。对MRF来说,相当于找到MRF参数,这些参数使得S在MRF分布下的概率最大,那么整个训练过程相当于找到参数θ,使得给定的训练数据的极大似然最大。给定数据集S,MRF的极大似然
。假设数据样本是独立且唯一的。就是说,他们是相互独立被从q中采样出来的。我们一般用极大似然来估计参数。对MRF来说,相当于找到MRF参数,这些参数使得S在MRF分布下的概率最大,那么整个训练过程相当于找到参数θ,使得给定的训练数据的极大似然最大。给定数据集S,MRF的极大似然 将θ从参数空间
将θ从参数空间 映射到了
映射到了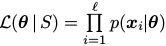 。极大化似然函数意味这极大化log似然
。极大化似然函数意味这极大化log似然
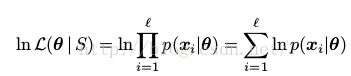 (1)
(1)
对于Gibbs分布,直接计算出使得似然函数最大的参数θ几乎是不可能的。因此,我们使用了一些估算的方法,例如梯度下降。
最大化似然函数相当于最大化未知分布q(即input)和分布由MRF估算出的分布p之间的距离,用KL-divergence表示:
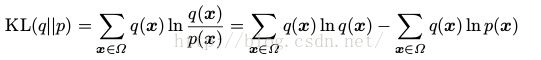 (2)
(2)
KL-divergence测量两个分布之间的差异。由于KL-divergence总是大于等于0的(0当且仅当两个分布相等),如上式,KL-divergence可以表示为q的熵和第二项之间的差。并且只有第二项依赖于θ。最大化log似然函数,相当于最小化KL-divergence。
梯度下降。我们无法直接找到参数使得似然函数最大,通常我们使用梯度下降的方法。
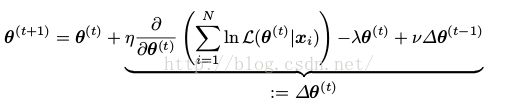 (3)
(3)
(一般都把λ和ν设成0吧,后面俩个是正则项)
隐藏参数.假设我们希望模拟一个m维的分布(例如,每个component都是一张图片中的m个像素)。通常,节点的个数大于m,并且不是所有的参数马尔可夫链中的参数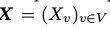 都需要和可视部分对应起来。我们将X分成两部分,可视部分(visible variables)
都需要和可视部分对应起来。我们将X分成两部分,可视部分(visible variables)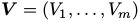 和隐藏部分(hidden variables
和隐藏部分(hidden variables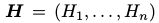 ,通过条件分布,即使可视部分的分布比较负责,我们也可以通过隐藏部分将他表示出来。这样,我们可以进行Gibbs采样获得(V,H)的联合概率分布,但通常我对边缘概率更感兴趣
,通过条件分布,即使可视部分的分布比较负责,我们也可以通过隐藏部分将他表示出来。这样,我们可以进行Gibbs采样获得(V,H)的联合概率分布,但通常我对边缘概率更感兴趣
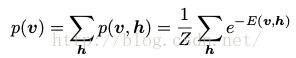 (4)
(4)
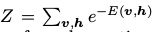 。其中可视参数相当于我们可以观察到的部分。
。其中可视参数相当于我们可以观察到的部分。
对隐藏参数求导.受限玻尔兹曼机就是由隐藏参数的MRF链,并且RBM的学习算法是基于log似然函数的梯度下降的。对于(4)式形式的模型来说,给定一个单独的训练集v,log似然函数如下所示(注意第一个v和第二个v的区别)
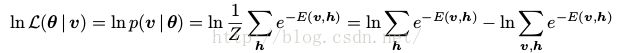 (5)
(5)
他的导数为
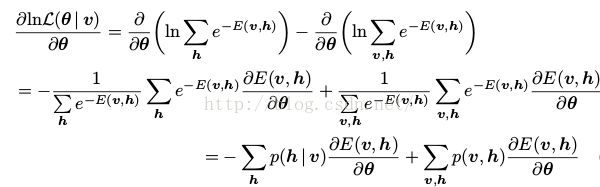 (6)
(6)
其中
注意,式(9)表示的是两个期望的差:第一项是给定了训练集,计算隐藏参数的条件概率下的能量函数的期望——p(h|v),第二项是在模型分布(联合分布)下的能量函数期望。如果只家求和的话,对每一个h,我们需要遍历所有的变量v的值,这样计算复杂度将是指数级的。为了减少计算复杂度,我们可以通过从相应的分布中进行采样来估算期望,这就用到了MCMC技术。
3马尔可夫链和马尔可夫链蒙特卡洛技术
马尔可夫链在RBM中占据来重要的地位,他为对复杂的分布进行采样提供了途径,例如Gibbs采样。
3.1马尔可夫链的定义和平稳分布
一个马尔可夫链是一个时间离散的随机过程,它满足马尔可夫条件,即对于一组随机参数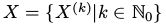 ,其中X(k)在集合Ω中取值,并且
,其中X(k)在集合Ω中取值,并且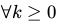 和
和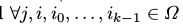 ,满足
,满足
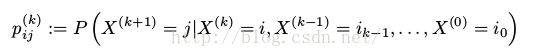 (7)
(7)
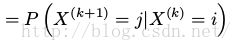 (8)
(8)
也就是说系统的下一个状态依赖于当前状态,而与之前的状态无关。如果对所有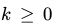 的
的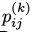 都有相同的值
都有相同的值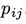 ,那么这条链被称为平稳分布的,矩阵
,那么这条链被称为平稳分布的,矩阵
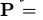
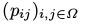 被称为平稳马尔可夫链的转移矩阵。
被称为平稳马尔可夫链的转移矩阵。
如果初始分布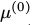 (即
(即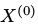 的概率分布)是由概率向量
的概率分布)是由概率向量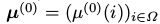 给出的,其中
给出的,其中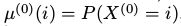 ,那么分布
,那么分布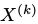 的概率分布
的概率分布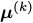 是由
是由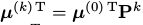 给出的。
给出的。
分布π满足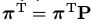 被称为成为马尔可夫链的平稳分布。如果任意时刻k的马尔可夫链达到了平稳分布
被称为成为马尔可夫链的平稳分布。如果任意时刻k的马尔可夫链达到了平稳分布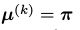 ,所有的状态序列就会收敛,即对所有
,所有的状态序列就会收敛,即对所有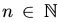
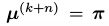 。分布π达到平稳分布的一个充分非必要条件是
。分布π达到平稳分布的一个充分非必要条件是
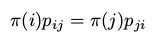 (13)
(13)
其中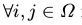 。(13)被称为细致平稳条件。
。(13)被称为细致平稳条件。
上述定义要求
- 马尔可夫链是不可约的,我们可以从Ω中的任意状态通过有限的 n 步转移到达另以状态。即
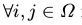
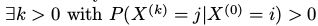
- 马尔可夫链是“非周期“的,如果满足对所有
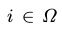 式
式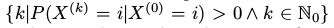 最公共的因子是1.
最公共的因子是1.
上述两个条件保证了有限状态空间下的马尔可夫链的收敛性,即对人以起始分布μ满足
其中d V是变量的距离。对两个有限状态空间下的分布α 和 β,他们的距离为
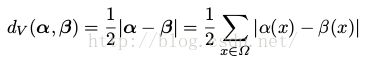 (9)
(9)
3.2Gibbs采样(关于非周期性和不可约的部分不太理解,感觉不太影响对整个RBM算法的理解,可以跳过)
Gibbs采样属于MH算法。MCMC算法对于多个随机变量算法复杂度较高,Gibbs是MCMC算法的改进,它从联合概率分布的产生样本。它的基本思想是给定了其他变量的状态下的条件概率分布,安顺序依次更新给每个变量的状态。
考虑MRF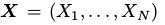 ,图G=(V,E),为了方便表示,设V={1,...,N}。随机变量Xi,i ∈ V从有限集合Λ中取值,
,图G=(V,E),为了方便表示,设V={1,...,N}。随机变量Xi,i ∈ V从有限集合Λ中取值,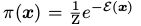 是X的联合概率分布。并且,我们假设MRF随着时间改变它的状态,设
是X的联合概率分布。并且,我们假设MRF随着时间改变它的状态,设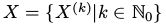 是一个
是一个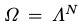 在中取值的马尔可夫链,其中
在中取值的马尔可夫链,其中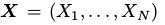 表示MRF在时刻k时的状态。在每一次转移过程中,我们以概率q(i)选择一个随机变量Xi,i ∈ V。其中q(i)由一个V上的概率分布q给出,q是严格大于0的。在其他所有变量
表示MRF在时刻k时的状态。在每一次转移过程中,我们以概率q(i)选择一个随机变量Xi,i ∈ V。其中q(i)由一个V上的概率分布q给出,q是严格大于0的。在其他所有变量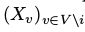 已知的条件下求得状态
已知的条件下求得状态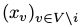 ,即
,即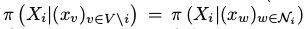 ,那么我们可以依次采样出Xi的新的值。
,那么我们可以依次采样出Xi的新的值。
举个列子:
因此对于MRF中的两个状态x,y的,他们的转移概率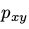 (其中x不等于y)如下所示
(其中x不等于y)如下所示
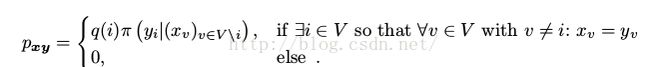 (10)
(10)
状态x保持不变的概率为:
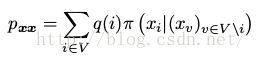 (11)
(11)
解释如下(摘自本篇博文:LDA-math-MCMC 和 Gibbs Sampling(2))
—————————我是引用的分割线————————
如图,在 x=x1 这条平行于 y轴的直线上,如果使用条件分布 p(y|x1)做为任何两个点之间的转移概率,那么任何两个点之间的转移满足细致平稳条件。同样的,如果我们在 y=y1 这条直线上任意取两个点 A(x1,y1),C(x2,y1),也有如下等式
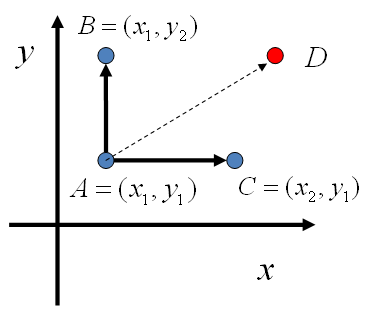
平面上马氏链转移矩阵的构造
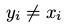 于是我们可以如下构造平面上任意两点之间的转移概率矩阵Q
于是我们可以如下构造平面上任意两点之间的转移概率矩阵Q

—————————我是引用的分割线————————
我们很容易可以看出,MRF下的联合分布π是马尔可夫链的定义的一个稳定的分布,它是由这些转移概率规定的。由细致平稳条件所满足的条件可以看出:对x=y那么我们可以直径运用细致平稳条件;如果x中y至少一个变量不一致,那么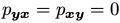 。假设x和y中只有变量Xi不同,即对
。假设x和y中只有变量Xi不同,即对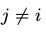 那么
那么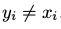 ,
,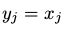 ,那么就满足
,那么就满足
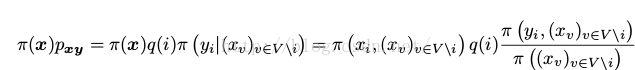 (12)
(12)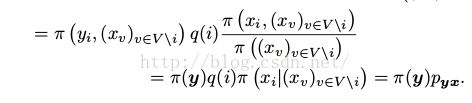
(上式中的几个解释:
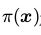 :状态x
:状态x
q(i):每一次转移过程中,我们以概率q(i)选择一个随机变量Xi,i ∈ V。其中q(i)由一个V上的概率分布q给出,q是严格大于0的。
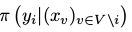 :已知状态x下的所有变量的值,将第i维的坐标从xi转移到yi
:已知状态x下的所有变量的值,将第i维的坐标从xi转移到yi
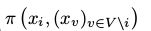 同上)
同上)
因为π是严格大于0的,因此单个变量的条件概率分布也是严格大于0的。因此,在每次转移步骤中在每个状态x i ∈ Λ选择一个变量Xi,那么可以在有限的步骤中,使整条链可以此从某一状态的达到其他任意状态(注意此时马尔可夫链必须满足是联通的,即不可约的)。并且由于条件概率分布是严格大于o的,即对所有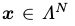 有
有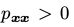 ,因此马尔可夫链是非周期的。非周期性和不可约性保证来整条链可以收敛到平稳状态π。
,因此马尔可夫链是非周期的。非周期性和不可约性保证来整条链可以收敛到平稳状态π。
在实际应用中,要进行更新的单个随机变量通常不是随机选择的,而是按照实现定义好的顺序。对应的算法一般成为周期Gibbs采样。如果P是转移矩阵,周期Gibbs采样的收敛到平稳分布的概率由如下约束条件:
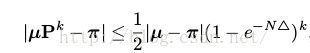 (13)
(13)
其中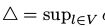 且
且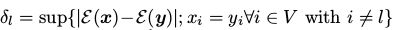
上式中u是初始的分布,是任意的。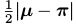 是(9)中定义的变量的距离。
是(9)中定义的变量的距离。
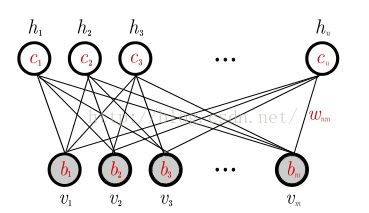
4 Restricted Boltzmann Machines
一个RBM是一个二分图。如图1,它由m个可视节点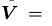
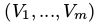 和n个隐藏节点构成
和n个隐藏节点构成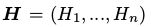 。在二值RBM中,对任意变量
。在二值RBM中,对任意变量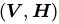
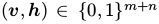 ,联合概率分布
,联合概率分布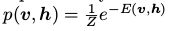 ,其中能量函数
,其中能量函数
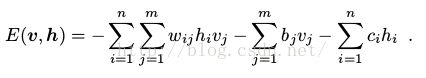 (14)
(14)
,对所有与的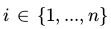 和
和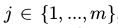
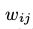 是连接
是连接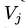 和
和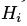 的边的权值,
的边的权值,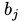 和
和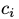 分别是第j个可视节点和第i个隐藏界的变量的偏移量。
分别是第j个可视节点和第i个隐藏界的变量的偏移量。
图1
RBM的图结构中,只有隐藏层和可视层之间由连接,同一层的两个变量之间没有连接。这意味着给定可视变量的状态,隐藏变量是相互独立的。反之亦然。
由于层内没有连接,我们可以很容易的计算出边缘概率
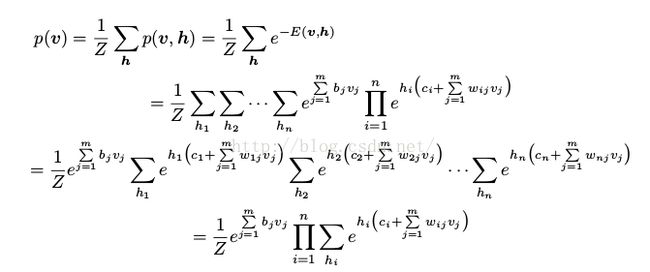
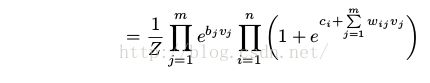 (15)
(15)
由该等式,我们可以看出为什么RBM可以被视为一个专家乘积系统(专家乘积系统中,可视部分的独立成分中的每个“专家”以乘积的形式结合起来)。
任意分布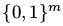 上的分布可以用有m个可视节点和k+1个隐藏节点的RBM进行很好的建模,其中k代表目标分布的支持集(support set)的基(cardinality),即,从
上的分布可以用有m个可视节点和k+1个隐藏节点的RBM进行很好的建模,其中k代表目标分布的支持集(support set)的基(cardinality),即,从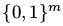 中的非0的输入元素的数量。
中的非0的输入元素的数量。
RBM可以理解为一个随机的神经网络,其中节点和边代表了神经元和类神经连接。单个变量的条件概率可以理解为一个(随机)神经元的燃烧率(firing rate)(应用了sigmoid函数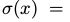
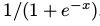 ):
):
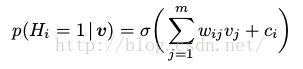 (16)
(16)
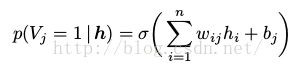 (17)
(17)
证明如下:
用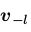 代表除了第l个可视节点的其他所有可视节点的状态,我们定义
代表除了第l个可视节点的其他所有可视节点的状态,我们定义
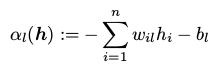 (18)
(18)
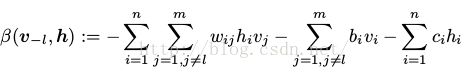 (19)
(19)
那么
其中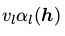 代表所有所有包括
代表所有所有包括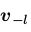 的项,那么
的项,那么
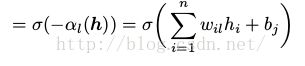 (20)
(20)
同理
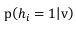 =
= (21)
(21)
层内节点之间的独立性使得Gibbs采样异常的简单:同一层的所有变量是联合(jointly)的采样的,而不是一个接着一个(subsequently)的对所有变量进行采样。因此,Gibbs采样可以在两个子步骤之间进行:利用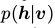 给隐藏神经元采集一个新的状态 h,然后利用
给隐藏神经元采集一个新的状态 h,然后利用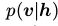 采集一个状态v。
采集一个状态v。
正如之前提到的,一个RBM可以被重新理解为一个非线性的前向传导(feed-forward)的神经网络,这样的华,RBM可以被视作一个决策函数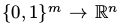 ,这个决策函数将
,这个决策函数将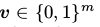 银蛇到了
银蛇到了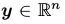 ,其中
,其中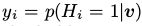 。这样,我们将可视部分映射到了在可视条件下的隐藏神经元的期望。
。这样,我们将可视部分映射到了在可视条件下的隐藏神经元的期望。
4.1 The Gradient of the Log-Likelihood
MRF的log似然函数的导数被写成两个期望的和,见式(6).对于RBMs,(6)的第一项(即在给定训练样本v下的隐藏变量的条件分布的期望的能量梯度)可以很方便的计算出来。例如,对参数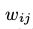 我们可以得到
我们可以得到
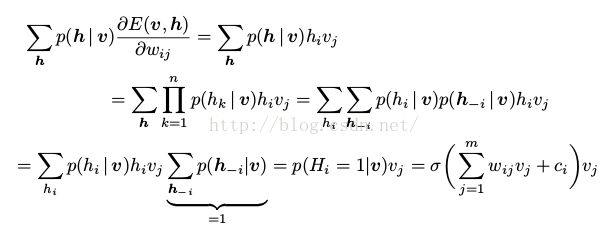 (21)
(21)
(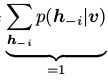 是因为层内相互独立,给定了v,我们只需要将第i维的状态转移,其他维是不变的,因此他们的概率之和为1)
是因为层内相互独立,给定了v,我们只需要将第i维的状态转移,其他维是不变的,因此他们的概率之和为1)
(6)中第二项可以写作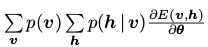 或者
或者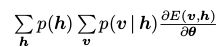 。我们可以对内层的和使用相同的方法来减少计算的复杂度。但是它的计算复杂度还是很大(求外层的和时,我们仍然需要循环
。我们可以对内层的和使用相同的方法来减少计算的复杂度。但是它的计算复杂度还是很大(求外层的和时,我们仍然需要循环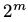 或者
或者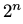 次)
次)
对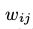 求导
求导
 (22)
(22)
通常对一个训练集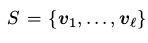 ,我们求上式的均值
,我们求上式的均值
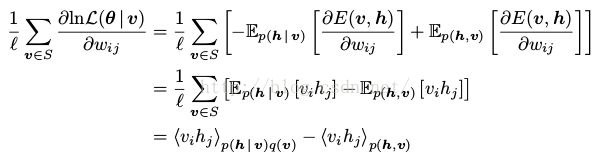 (23)
(23)
其中q表示经验分布(empirical distribution )。
——————————————分割线——————————————
关于为什么1/l被消掉了,之前引用给出的解释不太正确,Hiton在一篇文章
A fast learning algorithm for deep belief nets
中给出了解释
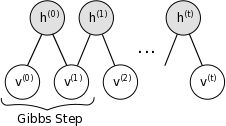
因为我们从真实的先验概率中进行采样,我们可以计算冲data的log概率的偏导数。对于第j层的H0,第i层的V0(图3).在logistic信念网络中,最大信念函数的对域一个单个的数据向量v0的梯度:
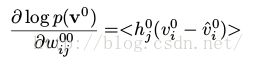 (2)
(2)
其中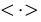 代表采样状态的平均值,
代表采样状态的平均值,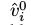 是单元i在通过隐藏状态随机的重建时,将会被激活的概率。用第一个隐藏层采样得到的二值状态H0来计算第二个隐藏层的后验分布V1,这个过程和重建数据的过程一样,所以
是单元i在通过隐藏状态随机的重建时,将会被激活的概率。用第一个隐藏层采样得到的二值状态H0来计算第二个隐藏层的后验分布V1,这个过程和重建数据的过程一样,所以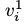 是从概率为
是从概率为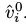 伯努里随机变量中采样得到的。那么整个学习过程如下
伯努里随机变量中采样得到的。那么整个学习过程如下
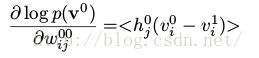 (3)
(3)
从(2)到(3)的转换中,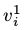 对
对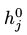 依赖并不会对上式中的导数造成问题,这是因为
依赖并不会对上式中的导数造成问题,这是因为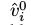 是
是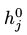 条件概率(
条件概率(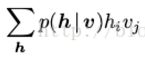
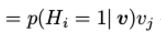 )下的期望(注意导数的原理,KL距离,还有第一个v和第二个v的意义不一样)。因为权重是不变的,权重的全导数所有layer之间权重的导数之和
)下的期望(注意导数的原理,KL距离,还有第一个v和第二个v的意义不一样)。因为权重是不变的,权重的全导数所有layer之间权重的导数之和
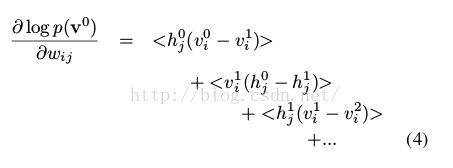
最后得到
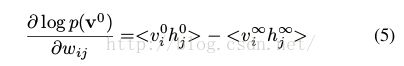
——————————————分割线—
—
—
———
————————
这样我们就可以得出:
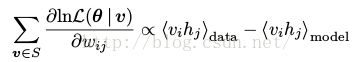 (24)
(24)
同(22),我们可以求出
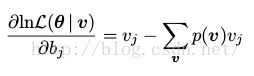 (25)
(25)
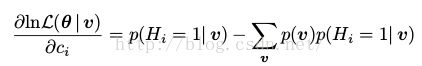 (26)
(26)
为了避免指数级的复杂度(对每一个可视变量遍历求和,或者对所有的隐藏变量乘上所有的可视节点,如(20))当计算第二项的时候,我们可以估算期望,这是通过从模型分布中采样实现的。我们使用来Gibbs采样,这需要让马尔可夫链足够长来保证它收敛的平稳分布。因为用这种MCMC方法来产生一个有效的算法计算的代价仍然非常大,下节我们将介绍另外的估算。
5 Approximating the RBM Log-Likelihood Gradient
所有的训练方法都要对log似然函数求梯度,接下来的这一节我们将介绍对比散度算法。
5.1 Contrastive Divergence
使用MCMC方法对log似然函数的梯度进行无偏估计通常需要进行多步采样。然而,实验证明只需要少量的步骤我们就可以得到理想的结果。于是衍生出了对比散度算法。
k步对比散步学习算法非常简单:我们只需要执行k步Gibbs采样(通常k=1)而不是对log似然函数的第二项进行估算(这需要执行马尔可夫链直至收敛)。通常我们用训练样本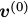 对Gibbs链进行初始化,在执行k步后就获得来样本
对Gibbs链进行初始化,在执行k步后就获得来样本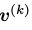 。每一步t都包含样本
。每一步t都包含样本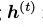 和
和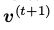 ,分别是由它是由
,分别是由它是由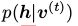 和
和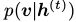 得到的。(6)中的梯度对于训练样本
得到的。(6)中的梯度对于训练样本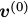 ,我们可以这样估算得到
,我们可以这样估算得到
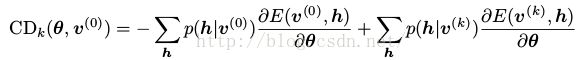 (27)
(27)
单个参数的的方向倒是可以通过单个样本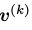 对p(v)估算期望得到(如式(22),(25),(26)),一个batch版本的CD-k算法如下
对p(v)估算期望得到(如式(22),(25),(26)),一个batch版本的CD-k算法如下
因为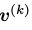 不是从平稳模型分布中采样得到的,这个估计是有偏的。可以看出,当时
不是从平稳模型分布中采样得到的,这个估计是有偏的。可以看出,当时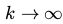 ,就近似于无偏的了。后面一些暂不翻译,用到再翻译
,就近似于无偏的了。后面一些暂不翻译,用到再翻译
![]() 。假设数据样本是独立且唯一的。就是说,他们是相互独立被从q中采样出来的。我们一般用极大似然来估计参数。对MRF来说,相当于找到MRF参数,这些参数使得S在MRF分布下的概率最大,那么整个训练过程相当于找到参数θ,使得给定的训练数据的极大似然最大。给定数据集S,MRF的极大似然
。假设数据样本是独立且唯一的。就是说,他们是相互独立被从q中采样出来的。我们一般用极大似然来估计参数。对MRF来说,相当于找到MRF参数,这些参数使得S在MRF分布下的概率最大,那么整个训练过程相当于找到参数θ,使得给定的训练数据的极大似然最大。给定数据集S,MRF的极大似然![]() 将θ从参数空间
将θ从参数空间![]() 映射到了
映射到了![]() 。极大化似然函数意味这极大化log似然
。极大化似然函数意味这极大化log似然![]() 都需要和可视部分对应起来。我们将X分成两部分,可视部分(visible variables)
都需要和可视部分对应起来。我们将X分成两部分,可视部分(visible variables)![]() 和隐藏部分(hidden variables
和隐藏部分(hidden variables![]() ,通过条件分布,即使可视部分的分布比较负责,我们也可以通过隐藏部分将他表示出来。这样,我们可以进行Gibbs采样获得(V,H)的联合概率分布,但通常我对边缘概率更感兴趣
,通过条件分布,即使可视部分的分布比较负责,我们也可以通过隐藏部分将他表示出来。这样,我们可以进行Gibbs采样获得(V,H)的联合概率分布,但通常我对边缘概率更感兴趣![]() 。其中可视参数相当于我们可以观察到的部分。
。其中可视参数相当于我们可以观察到的部分。![]() ,其中X(k)在集合Ω中取值,并且
,其中X(k)在集合Ω中取值,并且![]() 和
和![]() ,满足
,满足![]() 的
的![]() 都有相同的值
都有相同的值![]() ,那么这条链被称为平稳分布的,矩阵
,那么这条链被称为平稳分布的,矩阵![]()
![]() 被称为平稳马尔可夫链的转移矩阵。
被称为平稳马尔可夫链的转移矩阵。![]() (即
(即![]() 的概率分布)是由概率向量
的概率分布)是由概率向量![]() 给出的,其中
给出的,其中![]() ,那么分布
,那么分布![]() 的概率分布
的概率分布![]() 是由
是由![]() 给出的。
给出的。![]() 被称为成为马尔可夫链的平稳分布。如果任意时刻k的马尔可夫链达到了平稳分布
被称为成为马尔可夫链的平稳分布。如果任意时刻k的马尔可夫链达到了平稳分布![]() ,所有的状态序列就会收敛,即对所有
,所有的状态序列就会收敛,即对所有![]()
![]() 。分布π达到平稳分布的一个充分非必要条件是
。分布π达到平稳分布的一个充分非必要条件是![]() 。(13)被称为细致平稳条件。
。(13)被称为细致平稳条件。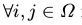
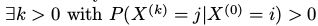
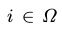 式
式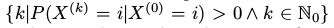 最公共的因子是1.
最公共的因子是1.![]() 于是我们可以如下构造平面上任意两点之间的转移概率矩阵Q
于是我们可以如下构造平面上任意两点之间的转移概率矩阵Q![]() 。假设x和y中只有变量Xi不同,即对
。假设x和y中只有变量Xi不同,即对![]() 那么
那么![]() ,
,![]() ,那么就满足
,那么就满足![]() :已知状态x下的所有变量的值,将第i维的坐标从xi转移到yi
:已知状态x下的所有变量的值,将第i维的坐标从xi转移到yi![]() 同上)
同上)![]() 代表采样状态的平均值,
代表采样状态的平均值,![]() 是单元i在通过隐藏状态随机的重建时,将会被激活的概率。用第一个隐藏层采样得到的二值状态H0来计算第二个隐藏层的后验分布V1,这个过程和重建数据的过程一样,所以
是单元i在通过隐藏状态随机的重建时,将会被激活的概率。用第一个隐藏层采样得到的二值状态H0来计算第二个隐藏层的后验分布V1,这个过程和重建数据的过程一样,所以![]() 是从概率为
是从概率为![]() 伯努里随机变量中采样得到的。那么整个学习过程如下
伯努里随机变量中采样得到的。那么整个学习过程如下![]() 对
对![]() 依赖并不会对上式中的导数造成问题,这是因为
依赖并不会对上式中的导数造成问题,这是因为![]() 是
是![]() 条件概率(
条件概率(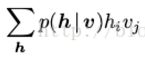
![]() )下的期望(注意导数的原理,KL距离,还有第一个v和第二个v的意义不一样)。因为权重是不变的,权重的全导数所有layer之间权重的导数之和
)下的期望(注意导数的原理,KL距离,还有第一个v和第二个v的意义不一样)。因为权重是不变的,权重的全导数所有layer之间权重的导数之和