暑假集训——递推 P - 折线分区域

P - 折线分区域

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。 

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。 

 

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。 

 

Sample Input

      
      
      
      

       
       
       
       2
1
2 
      
      
      
      

 

Sample Output

      
      
      
      

       
       
       
       2
7 
      
      
      
      

分析：

解题思路：

１递推递推，先分析下直线分割平面的情况，增加第n条直线的时候，跟之前的直线最多有n-1个交点，此时分出的部分多出了（n-1）+1；所以f[n]=f[n-1]+n-1+1;

２折线也是同理，f(1)=2,f(2)=7,先画好前面n-1条折线

当增加第n条拆线时，此时折线中的一条与图形的交点最多有2*（n-1）

因为n-1条折线相当于2*（n-1)条直线，那么一条折线就有2*2(n-1)个交点，

所以分出的部分多出了2*2（n-1）+1所以推出f(n)=f(n-1)+4*(n-1)+1,n>=2

还有f[n]=n(2n-1)+1,这是从递推公式中推出来的;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include<stdio.h>
int main()
{
    int t,n,i;
    long long  a[10010];
    scanf("%d",&t);
    while(t--)
    {
        a[0]=0,a[1]=2,a[2]=7;
        scanf("%d",&n);
        for(i=3;i<=n;i++)
            a[i]=a[i-1]+4*(i-1)+1;
        printf("%lld\n",a[n]);
    }
    return 0;
}

B - 三角形

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

用N个三角形最多可以把平面分成几个区域? 

 

Input

输入数据的第一行是一个正整数T(1<=T<=10000),表示测试数据的数量.然后是T组测试数据,每组测试数据只包含一个正整数N(1<=N<=10000).

 

Output

对于每组测试数据,请输出题目中要求的结果. 

 

Sample Input

      
      
      
      

       
       
       
       2 1 2 
      
      
      
      

 

Sample Output

      
      
      
      

       
       
       
       2 8 
      
      
      
      

3  三角形也去递推，f[1]=2;f[2]=8;增加的交点和增加的部分相同

平面本身是1部分．一个三角形将平面分成三角形内、外2部分，即增加了1部分，
两个三角形不相交时将平面分成3部分，相交时，交点越多分成的部分越多（见下图）；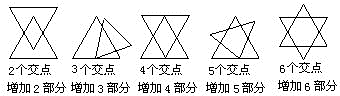

当增加第n个三角形时，三角形的一条边只能跟别的三角形的两条边相交

那么交点就增加了2(n-1),三条边就增加了3*2(n-1)个交点

所以推出f[n]=f[n-1]+6*(n-1);

另外，因为1个三角形时有2部分，所以n个三角形最多将平面分成的部分数是：
2+6×[1+2+…+（n-1）]=2+3n(n-1)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 

#include<stdio.h> int main() { int n,m,i,a[10010]; a[1]=2;a[2]=8; for(i=3;i<=10000;i++) a[i]=a[i-1]+6*(i-1); scanf("%d",&n); while(n--) { scanf("%d",&m); printf("%d\n",a[m]); } return 0; }

P - 折线分区域

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。 

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。 

 

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。 

 

Sample Input

       
       
       
       

        
        
        
        2
1
2 
       
       
       
       

 

Sample Output

       
       
       
       

        
        
        
        2
7 
       
       
       
       

分析：

解题思路：

１递推递推，先分析下直线分割平面的情况，增加第n条直线的时候，跟之前的直线最多有n-1个交点，此时分出的部分多出了（n-1）+1；所以f[n]=f[n-1]+n-1+1;

２折线也是同理，f(1)=2,f(2)=7,先画好前面n-1条折线

当增加第n条拆线时，此时折线中的一条与图形的交点最多有2*（n-1）

因为n-1条折线相当于2*（n-1)条直线，那么一条折线就有2*2(n-1)个交点，

所以分出的部分多出了2*2（n-1）+1所以推出f(n)=f(n-1)+4*(n-1)+1,n>=2

还有f[n]=n(2n-1)+1,这是从递推公式中推出来的;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include<stdio.h>
int main()
{
    int t,n,i;
    long long  a[10010];
    scanf("%d",&t);
    while(t--)
    {
        a[0]=0,a[1]=2,a[2]=7;
        scanf("%d",&n);
        for(i=3;i<=n;i++)
            a[i]=a[i-1]+4*(i-1)+1;
        printf("%lld\n",a[n]);
    }
    return 0;
}

B - 三角形

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit  Status

Description

用N个三角形最多可以把平面分成几个区域? 

 

Input

输入数据的第一行是一个正整数T(1<=T<=10000),表示测试数据的数量.然后是T组测试数据,每组测试数据只包含一个正整数N(1<=N<=10000).

 

Output

对于每组测试数据,请输出题目中要求的结果. 

 

Sample Input

       
       
       
       

        
        
        
        2 1 2 
       
       
       
       

 

Sample Output

       
       
       
       

        
        
        
        2 8 
       
       
       
       

3  三角形也去递推，f[1]=2;f[2]=8;增加的交点和增加的部分相同

平面本身是1部分．一个三角形将平面分成三角形内、外2部分，即增加了1部分，
两个三角形不相交时将平面分成3部分，相交时，交点越多分成的部分越多（见下图）；

当增加第n个三角形时，三角形的一条边只能跟别的三角形的两条边相交

那么交点就增加了2(n-1),三条边就增加了3*2(n-1)个交点

所以推出f[n]=f[n-1]+6*(n-1);

另外，因为1个三角形时有2部分，所以n个三角形最多将平面分成的部分数是：
2+6×[1+2+…+（n-1）]=2+6×

n(n-1)

2

=2+3n（n-1）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 

#include<stdio.h> int main() { int n,m,i,a[10010]; a[1]=2;a[2]=8; for(i=3;i<=10000;i++) a[i]=a[i-1]+6*(i-1); scanf("%d",&n); while(n--) { scanf("%d",&m); printf("%d\n",a[m]); } return 0; }