hdu4686 Arc of Dream
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 3354 Accepted Submission(s): 1055
1 ax*bx 0 0 0 0 0
0 ax*by ax 0 0 0 0
A=0 ay*bx 0 bx 0 0 0
0 0 1 0 1 0 0
0 0 0 1 0 1 0
Total Submission(s): 3354 Accepted Submission(s): 1055
Problem Description
An Arc of Dream is a curve defined by following function:
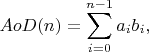
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
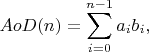
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
Input
There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Output
For each test case, output AoD(N) modulo 1,000,000,007.
Sample Input
1 1 2 3 4 5 6 2 1 2 3 4 5 6 3 1 2 3 4 5 6
Sample Output
4 134 1902
这题可以用矩阵快速幂做,先退出公式f[n]=f[n-1]+a[n-1]*b[n-1],
我们可以构造矩阵【f[n-1],a[n-1]*b[n-1],a[n-1],b[n-1],ay,by,ay*by】*A=【f[n],a[n]*b[n],a[n],b[n],ay,by,ay*by】,容易得到
1 0 0 0 0 0 0
1 ax*bx 0 0 0 0 0
0 ax*by ax 0 0 0 0
A=0 ay*bx 0 bx 0 0 0
0 0 1 0 1 0 0
0 0 0 1 0 1 0
0 1 0 0 0 0 1
然后直接求就行了。
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
typedef unsigned long long ll;
#define inf 99999999
#define pi acos(-1.0)
#define MOD 1000000007
struct matrix{
ll n,m,i;
ll data[9][9];
void init_danwei(){
for(i=0;i<n;i++){
data[i][i]=1;
}
}
};
matrix multi(matrix &a,matrix &b){
ll i,j,k;
matrix temp;
temp.n=a.n;
temp.m=b.m;
for(i=0;i<temp.n;i++){
for(j=0;j<temp.m;j++){
temp.data[i][j]=0;
}
}
for(i=0;i<a.n;i++){
for(k=0;k<a.m;k++){
if(a.data[i][k]>0){
for(j=0;j<b.m;j++){
temp.data[i][j]=(temp.data[i][j]+(a.data[i][k]*b.data[k][j])%MOD )%MOD;
}
}
}
}
return temp;
}
matrix fast_mod(matrix &a,ll n){
matrix ans;
ans.n=a.n;
ans.m=a.m;
memset(ans.data,0,sizeof(ans.data));
ans.init_danwei();
while(n>0){
if(n&1)ans=multi(ans,a);
a=multi(a,a);
n>>=1;
}
return ans;
}
int main()
{
ll n,m,i,j;
ll ax,bx,ay,by,a0,b0,a1,b1;
while(scanf("%llu",&n)!=EOF)
{
scanf("%llu%llu%llu",&a0,&ax,&ay);
scanf("%llu%llu%llu",&b0,&bx,&by);
if(n==0){
printf("0\n");continue;
}
matrix a;
a.n=a.m=7;
memset(a.data,0,sizeof(a.data));
a.data[0][0]=a.data[1][0]=a.data[4][2]=a.data[4][4]=a.data[5][3]=a.data[5][5]=a.data[6][1]=a.data[6][6]=1;
a.data[1][1]=ax*bx%MOD;
a.data[2][1]=ax*by%MOD;
a.data[2][2]=ax%MOD;
a.data[3][1]=ay*bx%MOD;
a.data[3][3]=bx%MOD;
matrix cnt;
cnt=fast_mod(a,n-1);
matrix ant;
ant.n=1;ant.m=7;
a1=((a0*ax)%MOD+ay)%MOD;
b1=((b0*bx)%MOD+by)%MOD;
ant.data[0][0]=a0*b0%MOD;
ant.data[0][1]=a1*b1%MOD;
ant.data[0][2]=a1%MOD;
ant.data[0][3]=b1%MOD;
ant.data[0][4]=ay%MOD;
ant.data[0][5]=by%MOD;
ant.data[0][6]=ay*by%MOD;
matrix juzhen;
juzhen=multi(ant,cnt);
printf("%llu\n",juzhen.data[0][0]%MOD);
}
return 0;
}