https://www.cnblogs.com/31415926535x/p/10363253.html
概述
图的连通性是图论中的一个基础知识点,算法很简单,但是所所涉及的基础知识点也很多,后悔当初离散数学没有好好的学,QAQ,,,
这篇主要是记录一下两种方法求强连通分量的算法,Tarjan和Kosaraju的模板,
算法
(具体的算法的证明和相关的内容来自这篇博客以及红书上的内容)
强连通分量即 Strongly Connected Component,一个有向图中的人一两点若能相互到达,即为强连通图,若不为强连通图,则改图肯定由若干个小的强连通图组成,即为强连通分量,例如
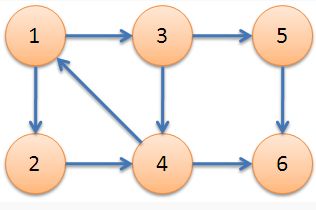
对于这个图,有三个强连通分量,{1,2,3,4},{5},{6},,,
Kosaraju算法
- 对原图进行一次深搜,计算出每一个节点被访问的次序(时间)st[i];
- 对逆图进行一次深搜,遍历的起点为第一步节点结束时间从大到小进行,同是做标记cnt2
- 最后标记值相同的点即为一个强连通分量,color[u]==color[v],说明u,v在用一个分量里,,(kuangbin的板子这里是用的belong[i]表示的)
Tarjan算法
Tarjan算法的思想:对于每一个强连通分量scc所构成的树一定为深搜时的dfs树,所以找到dfs树上的根即能确定一个scc
- dfn[i]记录的是节点i在深搜中的访问次序(时间戳)
- low[i]记录的是点i可以到达的访问时间的最早祖先
- Stack是记录节点的栈
1、深搜整个图,一路上标记dfn并把新节点压栈
2、对于一个节点i,如果low[i]==dfn[i],,说明他无法到达他的任何一个祖先
3、栈中i和i之后的点是相互可达的,所以可以组成一个极大强连通分量,可以整体弹出
4、low的求法:根据定义,如果点u访问一个新店v,那么u也可以到达low[v],所以可以用low[v]来尝试更新low[u];如果点u访问一个祖先k,那么就直接用dfn[k]尝试更新low[u];
(看那篇博客的图更好理解)
例题和模板
例题为红书上的推荐poj2189
题目分析
有这么一群牛,牛A可以认为牛B是受欢迎的,同时如果牛B认为牛C是受欢迎时,就可以理解为牛A认为牛C是受欢迎的,即这种关系具有传递性,然后问你这群牛中有多少头是被其他所有牛认为是受欢迎的。
抽象成图论的样子来理解就是:对于给定的一个有向图,u->v表示牛u认为牛v是受欢迎的,问你在这个图中有几个点是其他所有点可以到达的。
思路是先求出有向图的强连通分量,将同意分量的点“染色”成同一个编号,,然后“缩点”成一个DAG有向无环图,然后找出所有出度为0的点,如果这样的点只有一个,说明这个点是可以被其他的点到达的,同时也说明这个点(强连通分量)所包含的点也是原图中其他所有点可以到达的,答案就是这个强连通分量中点的个数;如果出度为0点有多个,及说明这些强连通分量块之间是没有可达的路径的,及原图中不存在任何一个其他所有点都能到达的点;
Kosaraju实现
//#include
#include
#include
#include
#include
#include
#define aaa cout<<233< '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
//kosaraju
struct edge
{
int to, next;
}edge1[maxn], edge2[maxn];
//edge1为原图,edge2为逆图
int head1[maxn], head2[maxn];
bool mark1[maxn], mark2[maxn];
int tot1, tot2;
int cnt1, cnt2;//cnt2即为强连通分量的个数scc
int st[maxn];//对原图进行dfs,点的结束时间从小到大的排序
int belong[maxn];//每个点属于那个连通分量的编号(0~cnt2-1)
int num;//中间变量,用来书某个连通分量中点的个数
int setnum[maxn];//强连通分量中点的个数,编号0~cnt2-1
void addedge(int u, int v)
{
edge1[tot1].to = v; edge1[tot1].next = head1[u]; head1[u] = tot1++;
edge2[tot2].to = u; edge2[tot2].next = head2[v]; head2[v] = tot2++;
}
void dfs1(int u)
{
mark1[u] = true;
for(int i = head1[u]; ~i; i = edge1[i].next)
if(!mark1[edge1[i].to])
dfs1(edge1[i].to);
st[cnt1++] = u;
}
void dfs2(int u)
{
mark2[u] = true;
++num;
belong[u] = cnt2;
for(int i = head2[u]; ~i; i = edge2[i].next)
if(!mark2[edge2[i].to])
dfs2(edge2[i].to);
}
void kosaraju(int n)
{
memset(mark1, false, sizeof mark1);
memset(mark2, false, sizeof mark2);
cnt1 = cnt2 = 0;
for(int i = 1; i <= n; ++i)
if(!mark1[i])
dfs1(i);
for(int i = cnt1 - 1; i >= 0; --i)
if(!mark2[st[i]])
{
num = 0;
dfs2(st[i]);
setnum[cnt2++] = num;
}
}
void init()
{
tot1 = tot2 = 0;
memset(head1, -1, sizeof head1);
memset(head2, -1, sizeof head2);
}
int main()
{
// freopen("233.in" , "r" , stdin);
// freopen("233.out" , "w" , stdout);
// ios_base::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);
int n, m;
while(scanf("%d%d", &n, &m) != EOF)
{
int u, v;
init();
while(m--)
{
scanf("%d%d", &u, &v);
addedge(u, v);
}
kosaraju(n);
int out[maxn];//缩点后每个强连通分量代表的点的出度
memset(out, 0, sizeof out);
for(int u = 1; u <= n; ++u)
for(int i = head1[u]; ~i; i = edge1[i].next)
{
int v = edge1[i].to;
if(belong[u] != belong[v])//缩点,同一编号的点即为同一个强连通分量
++out[belong[u]];
}
int flag = -1;//出度为零的点的编号
int num_ = 0;//出度为零的点的个数
for(int i = 0; i < cnt2; ++i)
if(!out[i])
{
flag = i;
++num_;
}
if(~flag && num_ == 1)
{
printf("%d\n", setnum[flag]);
}
else
{
printf("0\n");
}
}
return 0;
} Tarjan
//kaungbin的板子
//#include
#include
#include
#include
#include
#include
#define aaa cout<<233< '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
struct edge
{
int to, next;
}edge[maxn];
int head[maxn], tot;
int low[maxn], dfn[maxn], Stack[maxn], belong[maxn];
int index, top;
int scc;//强连通分量的个数
bool instack[maxn];
int num[maxn];//每个编号的强连通分量中点的个数
void addedge(int u, int v)
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
void tarjan(int u)
{
int v;
low[u] = dfn[u]= ++index;
Stack[top++] = u;
instack[u] = true;
for(int i = head[u]; ~i; i = edge[i].next)
{
v = edge[i].to;
if(!dfn[v])
{
tarjan(v);
if(low[u] > low[v])low[u] = low[v];
}
else if(instack[v] && low[u] > dfn[v])
low[u] = dfn[v];
}
if(low[u] == dfn[u])
{
++scc;
do
{
v = Stack[--top];
instack[v] = false;
belong[v] = scc;
++num[scc];
}while(v != u);
}
}
void solve(int n)
{
memset(dfn, 0, sizeof dfn);
memset(instack, false, sizeof instack);
memset(num, 0, sizeof num);
index = scc = top = 0;
for(int i = 1; i <= n; ++i)
if(!dfn[i])
tarjan(i);
}
void init()
{
tot = 0;
memset(head, -1, sizeof head);
}
int main()
{
// freopen("233.in" , "r" , stdin);
// freopen("233.out" , "w" , stdout);
// ios_base::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);
int n, m;
while(scanf("%d%d", &n, &m) != EOF)
{
int u, v;
init();
while(m--)
{
scanf("%d%d", &u, &v);
addedge(u, v);
}
solve(n);
int out[maxn];
memset(out, 0, sizeof out);
for(int u = 1; u <= n; ++u)
for(int i = head[u]; ~i; i = edge[i].next)
{
int v = edge[i].to;
if(belong[u] != belong[v])
++out[belong[u]];
}
int flag = -1;
int num_ = 0;
for(int i = 1; i <= scc; ++i)
if(!out[i])
{
flag = i;
++num_;
}
if(~flag && num_ == 1)
{
printf("%d\n", num[flag]);
}
else
{
printf("0\n");
}
}
return 0;
} //红书的板子,感觉不太友好,虽然看着舒服,但是没有上一个板子灵活,而且使用vector实现,耗时稍大
//#include
#include
#include
#include
#include
#include
#define aaa cout<<233< '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
struct scc
{
vector &color;
vector Stack;
int num_scc, colorcnt, curr, *instack, *dfn, *low, *info, *next, *to;
void dfs(int x)
{
dfn[x] = low[x] = ++curr;
Stack.push_back(x);
instack[x] = true;
for(int j = info[x]; j; j = next[j])
if(!instack[to[j]])
{
dfs(to[j]);
low[x] = min(low[x], low[to[j]]);
}
else if(instack[to[j]] == 1)
{
low[x] = min(low[x], dfn[to[j]]);
}
if(low[x] == dfn[x])
{
while(Stack.back() != x)
{
color[Stack.back()] = colorcnt;
instack[Stack.back()] = 2;
Stack.pop_back();
}
color[Stack.back()] = colorcnt++;
instack[Stack.back()] = 2;
Stack.pop_back();
++num_scc;
}
}
//edge为图, n为点数, ans为染色的结果,及编号, ansn为scc的个数
scc(const vector > &edge, int n, vector &ans, int &ansn):color(ans)
{
color.resize(n);
instack = new int[n];
dfn = new int[n];
low = new int[n];
info = new int[n];
next = new int[(int)edge.size() + 5];
to = new int[(int)edge.size() + 5];
fill_n(info, n, 0);
for(size_t i = 0; i < edge.size(); ++i)
{
to[i + 1] = edge[i].second;
next[i + 1] = info[edge[i].first];
info[edge[i].first] = i + 1;
}
fill_n(instack, n, 0);
colorcnt = 0;
curr = 0;
num_scc = 0;
for(int i = 0; i < n; ++i)
if(!instack[i])
dfs(i);
ansn = num_scc;
delete[] instack;
delete[] dfn;
delete[] low;
delete[] info;
delete[] next;
delete[] to;
}
};
int main()
{
// freopen("233.in" , "r" , stdin);
// freopen("233.out" , "w" , stdout);
// ios_base::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);
int n, m;
while(scanf("%d%d", &n, &m) != EOF)
{
int u, v;
vector > edge;
edge.clear();
while(m--)
{
scanf("%d%d", &u, &v);
--u;--v;
edge.push_back(make_pair(u, v));
}
vector ans;
ans.clear();
int ansn;
scc(edge, n, ans, ansn);
int out[maxn];
memset(out, 0, sizeof out);
for(size_t i = 0; i < edge.size(); ++i)
if(ans[edge[i].first] != ans[edge[i].second])
++out[ans[edge[i].first]];
int flag = -1;
int num = 0;
for(int i = 0; i < ansn; ++i)
if(!out[i])
{
flag = i;
++num;
}
if(~flag && num == 1)
{
int res = 0;
for(int i = 0; i < n; ++i)
if(ans[i] == flag)
++res;
printf("%d\n", res);
}
else
{
printf("0\n");
}
}
return 0;
} 总结
Tarjan和Kosaraju的时间复杂度基本相等,都为O(V + E),,,但是看很多人的建议是尽量用Tarjan做题,不易出现爆栈的情况,实际运行的时间也有时小一些,Kosaraju较容易理解;
求强连通分量是一些其他算法的基础,,例如2-sat;
(end)