双目测距（六）--三维重建及UI显示

原文：

http://blog.csdn.net/chenyusiyuan/article/details/5970799

在获取到视差数据后，利用 OpenCV 的 reProjectImageTo3D 函数结合 Bouquet 校正方法得到的 Q 矩阵就可以得到环境的三维坐标数据，然后利用 OpenGL 来实现三维重构。 

1．             reProjectImageTo3D 是怎样计算出三维坐标数据的？

 

图 22 

相信看过 OpenCV 第 12 章的朋友对上图中的 Q 矩阵不会陌生，根据以上变换公式，按理说 OpenCV 应该也是通过矩阵运算的方式来计算出三维坐标数据的，但实际上仔细查看源代码，会发现 cvReprojectImageTo3D 用了比较奇怪的方法来实现，主要代码如下：

 for( y = 0; y < rows; y++ )  
{  
         const float* sptr = (const float*)(src->data.ptr + src->step*y);   // 视差矩阵指针  
         float* dptr0 = (float*)(dst->data.ptr + dst->step*y), *dptr = dptr0;   // 三维坐标矩阵指针  
// 每一行运算开始时，用 当前行号y 乘以Q阵第2列、再加上Q阵第4列，作为初始值  
// 记 qq=[qx, qy, qz, qw]’  
         double qx = q[0][1]*y + q[0][3], qy = q[1][1]*y + q[1][3];      
         double qz = q[2][1]*y + q[2][3], qw = q[3][1]*y + q[3][3];     
…   
// 每算完一个像素的三维坐标，向量qq 累加一次q阵第1列  
// 即：qq = qq + q(:,1)  
         for( x = 0; x < cols; x++, qx += q[0][0], qy += q[1][0], qz += q[2][0], qw += q[3][0] )  
         {  
             double d = sptr[x];  
// 计算当前像素三维坐标  
// 将向量qq 加上 Q阵第3列与当前像素视差d的乘积，用所得结果的第4元素除前三位元素即可  
// [X,Y,Z,W]’ = qq + q(:,3) * d;   iW = 1/W; X=X*iW; Y=Y*iW; Z=Z*iW;  
             double iW = 1./(qw + q[3][2]*d);  
             double X = (qx + q[0][2]*d)*iW;  
             double Y = (qy + q[1][2]*d)*iW;  
             double Z = (qz + q[2][2]*d)*iW;  
             if( fabs(d-minDisparity) <= FLT_EPSILON )  
                 Z = bigZ;   // 02713     const double bigZ = 10000.;  
   
             dptr[x*3] = (float)X;  
             dptr[x*3+1] = (float)Y;  
             dptr[x*3+2] = (float)Z;  
         }  

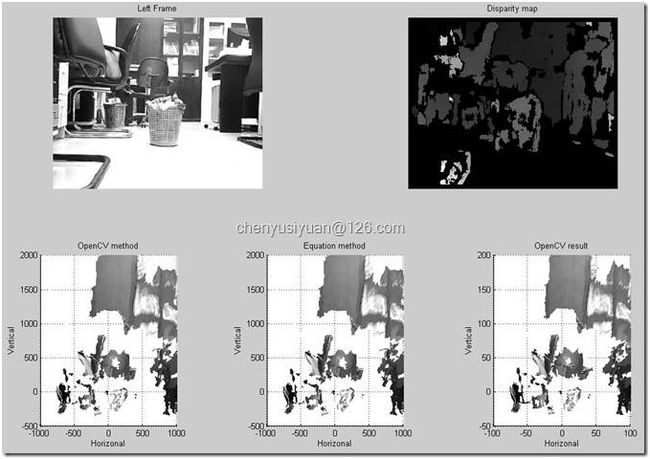
OpenCV 的这种计算方式比较令人费解，我的理解是可能这种方式的计算速度比较快。理论上，直接通过矩阵 Q 与向量 [x,y,d,1]’ 的乘积就可以得到相同的结果，下面用 Matlab 来验证一下两种方式是异曲同工的，用 Matlab 按照 OpenCV 计算方式得到的结果称为“ OpenCV method ”，直接按公式计算得到的结果称为“ Equation method ”，用 OpenCV 本身算出的三维坐标作为参考，程序代码如下 ：  

close all;clear all;clc   
im = imread('C:/Stereo IO Data/lfFrame_01.jpg');  
data = importdata('C:/Stereo IO Data/disparity_01.txt');  
r = data(1);    % 行数  
c = data(2);    % 列数  
disp = data(3:end); % 视差  
vmin = min(disp);  
vmax = max(disp);  
disp = reshape(disp, [c,r])'; % 将列向量形式的 disp 重构为 矩阵形式  
%  OpenCV 是行扫描存储图像，Matlab 是列扫描存储图像  
%  故对 disp 的重新排列是首先变成 c 行 r 列的矩阵，然后再转置回 r 行 c 列  
img = uint8( 255 * ( disp - vmin ) / ( vmax - vmin ) );  
q = [1. 0. 0. -1.5690376663208008e+002;...  
    0. 1. 0. -1.4282237243652344e+002;...      
    0. 0. 0. 5.2004731331639300e+002;...  
    0. 0. 1.0945105843175637e-002 0.]; % q(4,3) 原为负值，现修正为正值  
big_z = 1e5;  
pos1 = zeros(r,c,3);  
pos2 = zeros(r,c,3);  
for i = 1:r  
    qq = q*[0 i 0 1]';  
    for j = 1:c  
        if disp(i,j)>0  
        % OpenCV method  
            vec = qq + q(:,3)*disp(i,j);  
            vec = vec/vec(4);  
            pos1(i,j,:) = vec(1:3);  
        % Textbook method  
            tmp = q*[j,i,disp(i,j),1]'; % j 是列数，i 是行数，分别对应公式中的 x 和 y  
            pos2(i,j,:) = tmp(1:3)/tmp(4);  
        else  
            pos1(i,j,3) = big_z;  
            pos2(i,j,3) = big_z;  
        end  
        qq = qq + q(:,1);  
    end  
end  
subplot(221);  
imshow(im); title('Left Frame');  
subplot(222);  
imshow(img); title('Disparity map');  
% Matlab按OpenCV计算方式得到的三维坐标  
x = pos1(:,:,1);   
y = -pos1(:,:,2);  % 图像坐标系Y轴是向下为正方向，因此需添加负号来修正  
z = pos1(:,:,3);   
ind = find(z>10000);  % 以毫米为量纲  
x(ind)=NaN; y(ind)=NaN; z(ind)=NaN;  
subplot(234);  
mesh(x,z,y,double(im),'FaceColor','texturemap');  % Matlab 的 mesh、surf 函数支持纹理映射  
colormap(gray);   
axis equal;   
axis([-1000 1000 0 9000 -500 2000]);  
xlabel('Horizonal');ylabel('Depth');zlabel('Vertical'); title('OpenCV method');  
view([0 0]);  % 正视图  
% view([0 90]);   % 俯视图  
% view([90 0]);   % 侧视图  
% Matlab 按公式直接计算得到的三维坐标  
x = pos2(:,:,1);   
y = -pos2(:,:,2);   
z = pos2(:,:,3);   
ind = find(z>10000);  % 以毫米为量纲  
x(ind)=NaN; y(ind)=NaN; z(ind)=NaN;  
subplot(235);  
mesh(x,z,y,double(im),'FaceColor','texturemap');   
colormap(gray);   
axis equal;   
axis([-1000 1000 0 9000 -500 2000]);  
xlabel('Horizonal');ylabel('Depth');zlabel('Vertical'); title('Equation method');  
view([0 0]);  
% 读入OpenCV计算保存到本地的三维坐标作为参考  
data=importdata('C:/Stereo IO Data/xyz.txt');  
x=data(:,1); y=data(:,2); z=data(:,3);  
ind=find(z>1000);  % 以厘米为量纲  
x(ind)=NaN; y(ind)=NaN; z(ind)=NaN;  
x=reshape(x,[352 288])'; % 数据写入时是逐行进行的，而Matlab是逐列读取  
y=-reshape(y,[352 288])';   
z=reshape(z,[352 288])';  
subplot(236)  
mesh(x,z, y,double(im),'FaceColor','texturemap');  
colormap(gray);   
axis equal;axis([-100 100 0 900 -50 200]);  
xlabel('Horizonal');ylabel('Depth');zlabel('Vertical'); title('OpenCV result');  
view([0 0]);  

 

图 23 

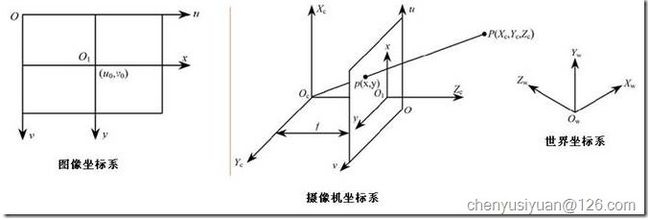
2．             为什么利用修正了的 Q 矩阵所计算得到的三维数据中， Y 坐标数据是正负颠倒的？

 

 

图 24 

这个问题我觉得可以从图像坐标系与摄像机坐标系的关系这一角度来解释。如上图所示，一般图像坐标系和摄像机坐标系都是以从左至右为X 轴正方向，从上至下为 Y 轴正方向 ，摄像机坐标系的 Z 轴正方向则是从光心到成像平面的垂线方向。因此，我们得到的三维坐标数据中 Y 轴数据的正负与实际是相反的，在应用时要添加负号来修正。

3．             如何画出三维重建图像和景深图像？ 

利用 cvReprojectImageTo3D 计算出的三维坐标数据矩阵一般是三通道浮点型的，需要注意的是这个矩阵存储的是三维坐标数据，而不是 RGB 颜色值，所以是不能调用 cvShowImage() 或者 OpenCV2.1 版的 imshow() 等函数来显示这个矩阵，否则就会看到这种图像：

图 25 

这里出现的明显的四个色块，其实应该是由三维坐标数据中的 X 轴和 Y 轴数据造成，不同象限的数据形成相应的色块。

要画出正确的三维重建图像，可以结合 OpenGL （可参考我的 学习笔记（ 15 ） ）或者 Matlab （例如保存三维数据到本地然后用 Matlab 的 mesh 函数画出，例程见本文问题 1 ；也可以考虑在 OpenCV 中调用 Matlab 混合编程）来实现。

深度图像的显示相对比较简单，只要从三维坐标数据中分离出来（可用 cvSplit() 函数），经过适当的格式转换（例如转换为 CV_8U 格式），就可用 cvShowImage() 或者 OpenCV2.1 版的 imshow() 等函数来显示了，伪彩色的深度图 也可以参考我的学习笔记（ 18 ） 问题 6 给出的例程 稍作修改即可实现。 

4．             怎样把 OpenGL 窗口的图像复制到 OpenCV 中用 IplImage 格式显示和保存？ 

在 学习笔记（ 15 ） 中详细给出了将 OpenCV 生成的 IplImage 图像和三维坐标数据复制到 OpenGL 中显示的例程，而在应用中，我们有时候也需要把 OpenGL 实时显示的三维图像复制到 OpenCV 中，用 IplImage 格式保存，以便和其它图像组合起来显示或保存为视频文件。这里给出相应的例程以供参考：

首先在创建 OpenGL 窗口时，显示模式要如下设置： 

[c-sharp] view plain copy print ?

1. //***OpenGL Window  
2. glutInit(&argc, argv);  
3. glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGB);  
4. glutInitWindowPosition(10,420);  
5. glutInitWindowSize(glWinWidth, glWinHeight);  
6. glutCreateWindow("3D disparity image");  

在循环中的调用：

 

[c-sharp] view plain copy print ?

1.     //////////////////////////////////////////////////////////////////////////  
2. // OpenGL显示  
3.         img3dIpl = img3d;  
4. load3dDataToGL(&img3dIpl);      // 载入需要显示的图像（视差数据）  
5. loadTextureToGL(&img1roi);      // 显示纹理  
6. glutReshapeFunc (reshape);          // 窗口变化时重绘图像  
7. glutDisplayFunc(renderScene);       // 显示三维图像  
8. glutPostRedisplay();                // 刷新画面（不用此语句则不能动态更新图像）  
9. loadPixel2IplImage(imgGL);          // 将 OpenGL 生成的像素值存储到 IplImage 中  

loadGLPixelToIplImage 函数定义： 

[c-sharp] view plain copy print ?

1. //////////////////////////////////////////////////////////////////////////  
2. // 将OpenGL窗口像素存储到 IplImage 中  
3. void  loadGLPixelToIplImage(IplImage* img)  
4. {  
5.     const int n = 3*glWinWidth*glWinHeight;   
6.     float *pixels = (float *)malloc(n * sizeof(GL_FLOAT));   
7.     IplImage *tmp = cvCreateImage(cvSize(glWinWidth, glWinHeight), 8, 3);  
8.     tmp->origin = CV_ORIGIN_BL;  
9. /* 后台缓存的图像数据才是我们需要复制的，若复制前台缓存会把可能的叠加在OpenGL窗口上的对象（其它窗口或者鼠标指针）也复制进去*/  
10.     glReadBuffer(GL_BACK);        
11.     glReadPixels(0, 0, glWinWidth, glWinHeight, GL_RGB, GL_FLOAT, pixels);  
12.     int k = 0;  
13.     for(int i = 0 ; i < glWinHeight; i++)  
14.     {  
15.         for(int j = 0 ; j < glWinWidth; j++,k+=3)  
16.         {  
17.             CvPoint pt = {j, glWinHeight - i - 1};  
18.             uchar* temp_ptr = &((uchar*)(tmp->imageData + tmp->widthStep*pt.y))[pt.x*3];  
19.             //OpenGL采用的是BGR格式，所以,读出来以后,还要换一下R<->B,才能得到RGB  
20.             temp_ptr[0] = pixels[k+2] * 255; //blue   
21.             temp_ptr[1] = pixels[k+1] * 255; //green  
22.             temp_ptr[2] = pixels[k] * 255;   //red  
23.         }  
24.     }     
25.     cvResize(tmp, img);  
26.     // 释放内存  
27.     free(pixels);  
28.     cvReleaseImage(&tmp);  
29. }  

 

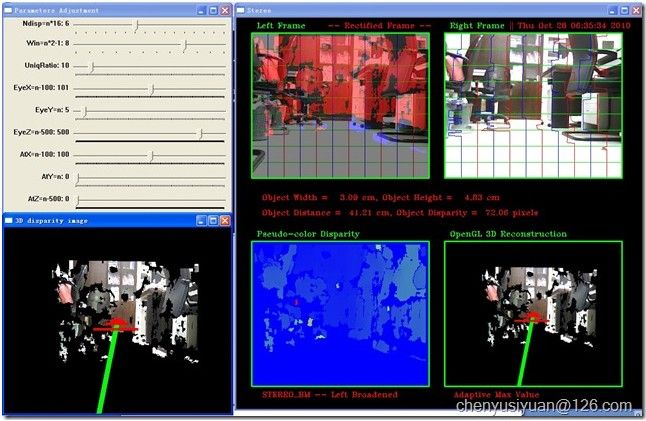
显示效果如下：

 

图26