ClownFeilong
ClownFeilong

51Nod 1352 集合计数 extend GCD 扩展欧几里得+找点




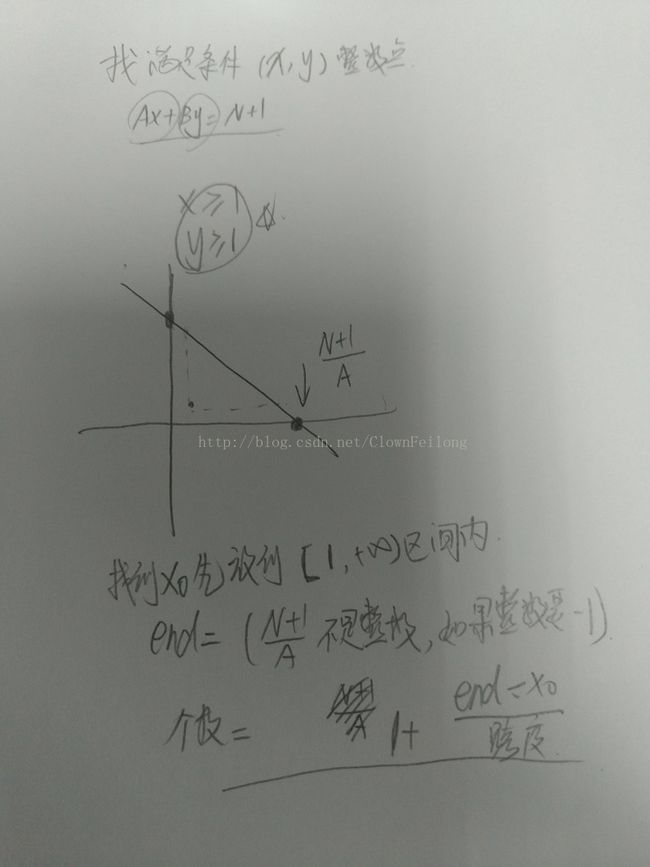
给出N个固定集合{1，N},{2,N-1},{3,N-2},...,{N-1,2},{N,1}.求出有多少个集合满足：第一个元素是A的倍数且第二个元素是B的倍数。

提示：

对于第二组测试数据，集合分别是：{1,10},{2,9},{3,8},{4,7},{5,6},{6,5},{7,4},{8,3},{9,2},{10,1}.满足条件的是第2个和第8个。


Input第1行：1个整数T（1<=T<=50000)，表示有多少组测试数据。 
第2 - T+1行：每行三个整数N，A,B（1<=N，A，B<=2147483647) Output对于每组测试数据输出一个数表示满足条件的集合的数量，占一行。 Sample Input 
2
5 2 4
10 2 3
Sample Output 
1
2

51Nod 1352 集合计数 extend GCD 扩展欧几里得+找点_第1张图片

#include
#include
#include
#include
#include
#include
#include

using namespace std;

long long t;
long long n, a, b;
long long gcd(long long x, long long y)
{
	return y == 0 ? x : gcd(y, x%y);
}

long long extgcd(long long a, long long b, long long &x, long long &y)
{
	if (b == 0)
	{
		x = 1;y = 0;
		return a;
	}

	long long r = extgcd(b, a%b, x, y);

	long long t = x;
	x = y;
	y = t - a / b*y;

	return r;
}


int main()
{
	scanf("%lld", &t);
	while (t--)
	{
		scanf("%lld %lld %lld", &n, &a, &b);
		long long x0, y0;
		n++;
		long long ans = gcd(a,b);	
		long long res = 0;
		if (n%ans == 0)
		{
			long long a1 = a / ans;
			long long b1 = b / ans;
			long long n1 = n / ans;
			extgcd(a1, b1, x0, y0);
			x0 *= n1;
			y0 *= n1;
			if (x0 <= 1)
			{
				long long aaa = (1 - x0) % b1;
				x0 = 1-aaa + (aaa == 0 ? 0 : b1);
			}
			else
				x0 = 1 + (x0-1)%b1;

			long long end = n / a - (n%a == 0 ? 1 : 0);
			if(x0<=end)
				res = 1+ (end - x0) / b1;
		}

		printf("%lld\n", res);
	}

	return 0;
}


你可能感兴趣的:(数论)

  • 致良知之寄诸用明书 BonSun
    众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
  • Python【math数学函数】 Alan_Lowe #Pythonpython
    Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • 算法设计与分析学习（6）——数论 罗塞菈桔梨萝柚 算法学习算法线性代数
    数论整除基本概念若aaa和bbb为整数，且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq，那么就说aaa可以整除bbb或是bbb被aaa整除，记作a∣ba|ba∣b。aaa也被称为bbb的约数，bbb也被称为a的倍数。若bbb不能被aaa整除，则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1，且除了±1,±p±1,±p±1,±p外没有其他的约数
  • 数论——欧几里得算法 NarutoTime 数论算法c++数据结构c语言
    1.欧几里得简介    欧几里得（希腊文：Ευκλειδης，约公元前330年—公元前275年），古希腊数学家，被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础，在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于：求解a和b的最大公约数。最大公约数英文为：Gre
  • 数论——扩展欧几里得算法 NOI_yzk
    欧几里得&拓展欧几里得（Euclid&Extend-Euclid）欧几里得算法（Euclid）背景：欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。——百度百科代码：递推的代码是相当的简洁：intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析：方法说了是辗转相除法，自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈？实际上在
  • 数论学习1（欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术） new出新对象！ 数学数算法学习
    目录1.唯一分解定理2.欧几里德算法（求最大公约数）3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少，(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式，乘法逆元，费马小定理今天也是小小的开始学习数论方面的知识了，首先数论的入门章节必然
  • Collatz 猜想和 Python 不连续小姐
    PythonDay4:CollatzConjecture原来总有学生问我，微积分有什么用啊，我说如果微积分学好了，也许抽象代数和数论就能学好，那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem，费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
  • 初等数论--整除--带余除法 WeidanJi 初等数论数学密码学信息安全
    初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论（整除+同余+原根），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。我整理成一个系列：初等数论，方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0，∃c∈Z,使a=bc,则称b整除a
  • 河南萌新2024第四场 Pown_ShanYu 算法数据结构
    C岗位分配题目大意：有n个岗位，m位志愿者，每个岗位至少需要a个志愿者，并且可以有志愿者可以空闲下来作预备，给出可能的分配情况总数思路：首先将每个岗位分配好至少需要的志愿者，再将剩下的人进行分配，那就满足球同盒不同模型（允许空盒），可用隔板法进行分配，需要额外开设一个空闲岗位用来预备，那么按照4个人去4个岗位，那么为c73，具体操作可看数论模板中发布的隔板法问题，递归求组合数Solved：intn
  • 【读书笔记】吴非《致青年教师》(4) 冬儿菇凉
    一、精要摘录(48——106页)1.教育教学不能“唯分数论“，比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感，心中有学生才会很在意学生对他的态度，在意学生的接受度。3.作为教师，你要善于向学生问出有意思的问题。4.教育就是要培养好习惯，教是为了达到不需要教学生，不需要老师教了是教学的成功，也是教师的职业追求。5.教师是学习者，在学习上教师首先要郑重其事，学生才有可能养成敬
  • 【代码随想录算法训练营Day39】62.不同路径；63. 不同路径 II 想做一只潜水的猪 算法
    文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难
  • 算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II memolaner 算法训练营算法动态规划数据结构c++python
    今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难想到。代码随想录视频讲解：动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示，第一直觉就是一个组合数的问题，学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成，重点是把二维的动态规划
  • 牛客周赛 Round 35（A,B,C,D,E,F,G） 邪神与厨二病 牛客算法暴力c++数论滑动窗口单调队列贪心构造
    这场简单，甚至赛时90分钟不到就AK了。比赛链接，队友题解友链刚入住学校监狱，很不适应，最近难受的要死，加上最近几场CF打的都不顺利，san值要爆掉了，只能慢慢补题了。这场C是个滑动窗口，D是贪心，E是有点麻烦的构造，FG是数论。A小红的字符串切割思路：记录一下字符串长度，然后从中间拆开。code：#include#include#includeusingnamespacestd;strings;
  • 算法——数论——同余 戏拈秃笔 数据结构与算法（java版）算法
    目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余：若m（正整数），a和b是整数，a%m==b%m，或(a-b)%m==0，记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程，解法看下面第一题二元线性丢番图方程逆：的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
  • pku acm 题目分类 moxiaomomo 算法数据结构numbers优化calendarcombinations
    1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
  • C++STL之Queue容器 芯片烧毁大师 数据结构C++c++开发语言
    C++STL之Queue容器1.再谈队列回顾一下之前所学的队列，队列和栈不同，队列是一种先进先出的数据结构，STL的队列内容极其重要，虽然内容较少但是请务必掌握，STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件：#include3.初始化格式为：**explicit**queue(**const**container_type&ctnr=container_t
  • 数字签名算法MD5withRSA Just_Paranoid 技术流Clipmd5rsasignatrue
    数字签名MD5withRSA，：将正文通过MD5数字摘要后，将密文再次通过生成的RSA密钥加密，生成数字签名，将明文与密文以及公钥发送给对方，对方拿到私钥/公钥对数字签名进行解密，然后解密后的，与明文经过MD5加密进行比较，如果一致则通过使用Signature的API来实现MD5withRSARSA原理：RSA算法基于一个十分简单的数论事实，将两个大素数相乘十分容易，但反过来想要对其乘积进行因式分
  • 2301: 不定方程解的个数 jht0105 算法
    题目描述输出不定方程解的个数。在数学中，不定方程是数论中的一个重要课题，在各种比赛中也常常出现.对于不定方程，有时我们往往只求非负整数解，现有方程ax+by+c=0，其中x、y为未知量且不超过10000，当给定a、b、c的值以后，可求出n组x、y的非负整数解，n>=0，,其中a，b，c均为[-10000,10000].输入描述一行，三个空格隔开的整数，为a、b、c的值。输出描述一个整数，为合法的解
  • python伯努利多项式 微小冷 #sympypython开发语言sympy伯努利数排列组合符号计算
    文章目录伯努利数和多项式sympy实现伯努利数是一种在数学、物理和工程中广泛应用的特殊数列，以瑞士数学家雅各布·伯努利（JacobBernoulli）的名字命名，并在许多领域中发挥重要作用。在数学中，它们与斐波那契数列、卡塔兰数、贝尔数等数列有密切联系，可以用于解决循环问题、组合问题和递推关系等数学问题。伯努利数和多项式伯努利(Bernoulli)数是一组在数论和复分析中出现的数，与伯努利多项式有
  • 二次剩余问题x的求解及代码实现（python） JustGo12 数论安全1024程序员节
    一、问题引入二次剩余是数论基本概念之一。它是初等数论中非常重要的结果，不仅可用来判断二次同余式是否有解，还有很多用途。C.F.高斯称它为算术中的宝石，他一人先后给出多个证明。[1]研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用，包括从噪音工程学到密码学以及大数分解。即关于方x^2≡a(modp)对于这个方程，求出满足条件的x。二、x的求解在上述问题下，根据p值的不同性质，可以
  • 【数论】exgcd 扩展欧几里得算法 Texcavator 数论算法
    参考：exgcd详解-zzt1208-博客园(cnblogs.com)exgcd（扩展欧几里得算法），用来求形如ax+by=gcd(a,b)ax+by=gcd(a,b)ax+by=gcd(a,b)（a,ba,ba,b为常数）的方程的一组整数解。（如果不确定等号右边是不是gcd，可以先当做gcd，求出来之后验证，是的话就是解，不是的话就不是解）推导见上面的链接，这篇只放个板子codeintexgcd
  • 2021-07-30 RX-0493
    学了一会数论，好难1.乘法逆元：a/b%p,若a/b在进行取模运算时，会出现精度问题，而且模运算对除法不适用，（没有分配律，大概就这意思）而求出乘法逆元后，可以把原式变为a*x%p的形式，且值不变。a*x≡1（modp）中，a,p为已知量，则x为a的乘法逆元。例题：乘法逆元设p=k*i+r,(1usingnamespacestd;constintN=20000530;intn,p,inv[N];i
  • 同余数论性质 clmm_ 算法
    同余概念当a%m==b%m，说明a和b同余，写作若a≡b(modm)性质衍生出几条性质1.m|abs(a-b)，即|a-b|是m的倍数。（注意，0是任何数的倍数）2.当a≡b(modm)，c≡d(modm)，有ac≡bd(modm)有a+c≡b+d(modm)有a-c≡b-d(modm)证明如下
  • 读《爱心与教育》第八天 皮_小皮
    作为一名教师，尤其是班主任老师，“培优转差”是教育工作的一项重要内容，读了李镇西老师的《爱心与教育》，自己受到不小的启发，对“优生”的培养和后进生的转化有了新的认识和思考。对“优生”的重新认识——李老师说：“优生”当然应该是指品学兼优的学生，但在现在不少教师、家长的眼中，所谓“优生”更多的是指学习成绩拔尖的学生（即尖子生）。的确，在升学竞争和应试教育的大环境下，很多教育者都以分数论英雄，对“优生”
  • RSA算法 superdont 图像加密算法java服务器
    RSA算法是一个非对称加密算法，它依赖于数论中的大整数因数分解问题的困难性。在RSA中，加密和解密使用不同的密钥，分别称为公钥和私钥。RSA算法的基本原理包括以下几个步骤：密钥生成：a.选择两个大的质数(p)和(q)。b.计算它们的乘积(n=pq)，n的长度就是密钥长度。c.计算欧拉函数(\phi(n)=(p-1)(q-1))。d.选择一个整数(e)，使得(1
  • 日精进110天 金八力韩英雪
    敬爱的老师，智慧的班主任，亲爱的跃友们：大家好！我是来自山峰教外教育的韩英雪，今天是我的日精进行动第110天，给大家分享我今天的进步，我们互相勉励，携手前行。每天进步一点点，距离成功便不远。1、比学习:个体身心发展的规律。顺序性，阶段性，不平衡性，互补性，个别差异性和整体性。个体身心发展的能动动因主要由内发论，外数论多因素互相作用论。其中内发论的代表人物包括孟子，弗洛伊德，威尔逊，格赛尔，霍尔等外
  • [C语言]Day04作业：输出菱形,判断水仙花数,输出a = aaaaa MrDorli C语言学习c语言
    /*1.在屏幕上输出以下图案：*************************************************************************************2.求出0～999之间的所有“水仙花数”并输出。“水仙花数”是指一个三位数，其各位数字的立方和确好等于该数本身，如；153＝1＋5＋3?，则153是一个“水仙花数”。在数论中，水仙花数（Narciss
  • 信安数基2-同余方程 利賀田
    基本概念及一次同余式同余式是数论的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m|(a-b)，则称a与b对模m同余，记为a≡b(modm)，或记为a≡b(m)。这个式子称为模m的同余式，若m∤(a-b)，则称a、b对模m不同余，同余概念又常表达为：1.a=b+km(k∈Z)；2.a和b被m除时有相同的[余数]。同余式的记号由高斯(Gauss,C.F.)于1800年首创,发表在他的数论
  • 【数论】矩阵快速幂 Texcavator 数论矩阵算法数据结构
    参考：P3193[HNOI2008]GT考试题解放个板子structMartix{inta[30][30];//在这里修改矩阵的大小Martix(){memset(a,0,sizeof(a));}Martixoperator*(constMartix&B)const//乘法运算符重载{Martixres;for(inti=0;i>=1;a=a*a;}returnans;}
  • apache 安装linux windows 墙头上一根草 apacheinuxwindows
    linux安装Apache 有两种方式一种是手动安装通过二进制的文件进行安装，另外一种就是通过yum 安装，此中安装方式，需要物理机联网。以下分别介绍两种的安装方式     通过二进制文件安装Apache需要的软件有apr,apr-util,pcre  1，安装 apr        下载地址：htt
  • fill_parent、wrap_content和match_parent的区别 Cb123456 match_parentfill_parent
    fill_parent、wrap_content和match_parent的区别:   1）fill_parent   设置一个构件的布局为fill_parent将强制性地使构件扩展，以填充布局单元内尽可能多的空间。这跟Windows控件的dockstyle属性大体一致。设置一个顶部布局或控件为fill_parent将强制性让它布满整个屏幕。 2） wrap_conte
  • 网页自适应设计 天子之骄 htmlcss响应式设计页面自适应
    网页自适应设计        网页对浏览器窗口的自适应支持变得越来越重要了。自适应响应设计更是异常火爆。再加上移动端的崛起，更是如日中天。以前为了适应不同屏幕分布率和浏览器窗口的扩大和缩小，需要设计几套css样式，用js脚本判断窗口大小，选择加载。结构臃肿，加载负担较大。现笔者经过一定时间的学习，有所心得，故分享于此，加强交流，共同进步。同时希望对大家有所
  • [sql server] 分组取最大最小常用sql 一炮送你回车库 SQL Server
    --分组取最大最小常用sql--测试环境if OBJECT_ID('tb') is not null drop table tb;gocreate table tb( col1 int, col2 int, Fcount int)insert into tbselect 11,20,1 union allselect 11,22,1 union allselect 1
  • ImageIO写图片输出到硬盘 3213213333332132 javaimage
    package awt; import java.awt.Color; import java.awt.Font; import java.awt.Graphics; import java.awt.image.BufferedImage; import java.io.File; import java.io.IOException; import javax.imagei
  • 自己的String动态数组 宝剑锋梅花香 java动态数组数组
    数组还是好说，学过一两门编程语言的就知道，需要注意的是数组声明时需要把大小给它定下来，比如声明一个字符串类型的数组：String str[]=new String[10];    但是问题就来了，每次都是大小确定的数组，我需要数组大小不固定随时变化怎么办呢？  动态数组就这样应运而生，龙哥给我们讲的是自己用代码写动态数组，并非用的ArrayList 看看字符
  • pinyin4j工具类 darkranger .net
    pinyin4j工具类Java工具类 2010-04-24 00:47:00 阅读69 评论0 字号：大中小 引入pinyin4j-2.5.0.jar包: pinyin4j是一个功能强悍的汉语拼音工具包，主要是从汉语获取各种格式和需求的拼音，功能强悍，下面看看如何使用pinyin4j。 本人以前用AscII编码提取工具，效果不理想，现在用pinyin4j简单实现了一个。功能还不是很完美，
  • StarUML学习笔记----基本概念 aijuans UML建模
    介绍StarUML的基本概念，这些都是有效运用StarUML?所需要的。包括对模型、视图、图、项目、单元、方法、框架、模型块及其差异以及UML轮廓。         模型、视与图（Model, View and Diagram）        &
  • Activiti最终总结 avords Activiti id 工作流
    1、流程定义ID：ProcessDefinitionId，当定义一个流程就会产生。 2、流程实例ID：ProcessInstanceId，当开始一个具体的流程时就会产生，也就是不同的流程实例ID可能有相同的流程定义ID。 3、TaskId，每一个userTask都会有一个Id这个是存在于流程实例上的。 4、TaskDefinitionKey和（ActivityImpl activityId
  • 从省市区多重级联想到的，react和jquery的差别 bee1314 jqueryUIreact
    在我们的前端项目里经常会用到级联的select，比如省市区这样。通常这种级联大多是动态的。比如先加载了省，点击省加载市，点击市加载区。然后数据通常ajax返回。如果没有数据则说明到了叶子节点。   针对这种场景，如果我们使用jquery来实现，要考虑很多的问题，数据部分，以及大量的dom操作。比如这个页面上显示了某个区，这时候我切换省，要把市重新初始化数据，然后区域的部分要从页面
  • Eclipse快捷键大全 bijian1013 javaeclipse快捷键
    Ctrl+1 快速修复(最经典的快捷键,就不用多说了)Ctrl+D: 删除当前行 Ctrl+Alt+↓ 复制当前行到下一行(复制增加)Ctrl+Alt+↑ 复制当前行到上一行(复制增加)Alt+↓ 当前行和下面一行交互位置(特别实用,可以省去先剪切,再粘贴了)Alt+↑ 当前行和上面一行交互位置(同上)Alt+← 前一个编辑的页面Alt+→ 下一个编辑的页面(当然是针对上面那条来说了)Alt+En
  • js 笔记 函数 征客丶 JavaScript
    一、函数的使用 1.1、定义函数变量 var vName = funcation(params){ } 1.2、函数的调用 函数变量的调用：      vName(params); 函数定义时自发调用：(function(params){})(params); 1.3、函数中变量赋值 var a = 'a'; var ff
  • 【Scala四】分析Spark源代码总结的Scala语法二 bit1129 scala
    1. Some操作   在下面的代码中，使用了Some操作：if (self.partitioner == Some(partitioner))，那么Some(partitioner)表示什么含义？首先partitioner是方法combineByKey传入的变量， Some的文档说明：   /** Class `Some[A]` represents existin
  • java 匿名内部类 BlueSkator java匿名内部类
    组合优先于继承 Java的匿名类，就是提供了一个快捷方便的手段，令继承关系可以方便地变成组合关系 继承只有一个时候才能用，当你要求子类的实例可以替代父类实例的位置时才可以用继承。   在Java中内部类主要分为成员内部类、局部内部类、匿名内部类、静态内部类。 内部类不是很好理解，但说白了其实也就是一个类中还包含着另外一个类如同一个人是由大脑、肢体、器官等身体结果组成，而内部类相
  • 盗版win装在MAC有害发热，苹果的东西不值得买，win应该不用 ljy325 游戏applewindowsXPOS
    Mac mini 型号: MC270CH-A RMB:5,688   Apple 对windows的产品支持不好,有以下问题:   1.装完了xp,发现机身很热虽然没有运行任何程序！貌似显卡跑游戏发热一样，按照那样的发热量,那部机子损耗很大,使用寿命受到严重的影响!   2.反观安装了Mac os的展示机，发热量很小，运行了1天温度也没有那么高 &nbs
  • 读《研磨设计模式》-代码笔记-生成器模式-Builder bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /** * 生成器模式的意图在于将一个复杂的构建与其表示相分离，使得同样的构建过程可以创建不同的表示（GoF） * 个人理解： * 构建一个复杂的对象，对于创建者（Builder）来说，一是要有数据来源(rawData)，二是要返回构
  • JIRA与SVN插件安装 chenyu19891124 SVNjira
    JIRA安装好后提交代码并要显示在JIRA上，这得需要用SVN的插件才能看见开发人员提交的代码。 1.下载svn与jira插件安装包，解压后在安装包(atlassian-jira-subversion-plugin-0.10.1) 2.解压出来的包里下的lib文件夹下的jar拷贝到(C:\Program Files\Atlassian\JIRA 4.3.4\atlassian-jira\WEB
  • 常用数学思想方法 comsci 工作
      对于搞工程和技术的朋友来讲，在工作中常常遇到一些实际问题，而采用常规的思维方式无法很好的解决这些问题，那么这个时候我们就需要用数学语言和数学工具，而使用数学工具的前提却是用数学思想的方法来描述问题。。下面转帖几种常用的数学思想方法，仅供学习和参考   函数思想 　　把某一数学问题用函数表示出来，并且利用函数探究这个问题的一般规律。这是最基本、最常用的数学方法
  • pl/sql集合类型 daizj oracle集合typepl/sql
    --集合类型 /*   单行单列的数据，使用标量变量   单行多列数据，使用记录   单列多行数据，使用集合（。。。）   *集合：类似于数组也就是。pl/sql集合类型包括索引表（pl/sql table）、嵌套表（Nested Table）、变长数组（VARRAY）等 */ /*     --集合方法 &n
  • [Ofbiz]ofbiz初用 dinguangx 电商ofbiz
    从github下载最新的ofbiz（截止2015-7-13），从源码进行ofbiz的试用 1. 加载测试库 ofbiz内置derby，通过下面的命令初始化测试库 ./ant load-demo (与load-seed有一些区别)   2. 启动内置tomcat ./ant start 或 ./startofbiz.sh 或 java -jar ofbiz.jar &
  • 结构体中最后一个元素是长度为0的数组 dcj3sjt126com cgcc
    在Linux源代码中，有很多的结构体最后都定义了一个元素个数为0个的数组，如/usr/include/linux/if_pppox.h中有这样一个结构体： struct pppoe_tag {     __u16 tag_type;     __u16 tag_len;   &n
  • Linux cp 实现强行覆盖 dcj3sjt126com linux
    发现在Fedora 10 /ubutun 里面用cp -fr src dest，即使加了-f也是不能强行覆盖的，这时怎么回事的呢？一两个文件还好说，就输几个yes吧，但是要是n多文件怎么办，那还不输死人呢？下面提供三种解决办法。 方法一 我们输入alias命令，看看系统给cp起了一个什么别名。 [root@localhost ~]# aliasalias cp=’cp -i’a
  • Memcached(一)、HelloWorld frank1234 memcached
    一、简介 高性能的架构离不开缓存，分布式缓存中的佼佼者当属memcached，它通过客户端将不同的key hash到不同的memcached服务器中，而获取的时候也到相同的服务器中获取，由于不需要做集群同步，也就省去了集群间同步的开销和延迟，所以它相对于ehcache等缓存来说能更好的支持分布式应用，具有更强的横向伸缩能力。 二、客户端 选择一个memcached客户端，我这里用的是memc
  • Search in Rotated Sorted Array II hcx2013 search
    Follow up for "Search in Rotated Sorted Array":What if duplicates are allowed? Would this affect the run-time complexity? How and why? Write a function to determine if a given ta
  • Spring4新特性——更好的Java泛型操作API jinnianshilongnian spring4generic type
    Spring4新特性——泛型限定式依赖注入 Spring4新特性——核心容器的其他改进 Spring4新特性——Web开发的增强 Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC  Spring4新特性——Groovy Bean定义DSL Spring4新特性——更好的Java泛型操作API  Spring4新
  • CentOS安装JDK liuxingguome centos
    1、行卸载原来的： [root@localhost opt]# rpm -qa | grep java tzdata-java-2014g-1.el6.noarch java-1.7.0-openjdk-1.7.0.65-2.5.1.2.el6_5.x86_64 java-1.6.0-openjdk-1.6.0.0-11.1.13.4.el6.x86_64 [root@localhost
  • 二分搜索专题2-在有序二维数组中搜索一个元素 OpenMind 二维数组算法二分搜索
    1,设二维数组p的每行每列都按照下标递增的顺序递增。 用数学语言描述如下：p满足 (1),对任意的x1，x2，y，如果x1<x2,则p(x1,y)<p(x2,y); (2),对任意的x，y1,y2, 如果y1<y2,则p(x,y1)<p(x,y2); 2,问题： 给定满足1的数组p和一个整数k，求是否存在x0,y0使得p(x0,y0)=k? 3,算法分析： (
  • java 随机数 Math与Random SaraWon javaMathRandom
    今天需要在程序中产生随机数，知道有两种方法可以使用，但是使用Math和Random的区别还不是特别清楚，看到一篇文章是关于的，觉得写的还挺不错的，原文地址是 http://www.oschina.net/question/157182_45274?sort=default&p=1#answers 产生1到10之间的随机数的两种实现方式： //Math Math.roun
  • oracle创建表空间 tugn oracle
    create temporary tablespace TXSJ_TEMP   tempfile 'E:\Oracle\oradata\TXSJ_TEMP.dbf'   size 32m   autoextend on   next 32m maxsize 2048m   extent m
  • 使用Java8实现自己的个性化搜索引擎 yangshangchuan javasuperword搜索引擎java8全文检索
    需要对249本软件著作实现句子级别全文检索，这些著作均为PDF文件，不使用现有的框架如lucene，自己实现的方法如下： 1、从PDF文件中提取文本，这里的重点是如何最大可能地还原文本。提取之后的文本，一个句子一行保存为文本文件。 2、将所有文本文件合并为一个单一的文本文件，这样，每一个句子就有一个唯一行号。 3、对每一行文本进行分词，建立倒排表，倒排表的格式为：词=包含该词的总行数N=行号
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他