Pytorch实现基本循环神经网络RNN
RNN
Recurrent Neural networks(Rumelhart, 1986) 主要用来处理序列型数据,具有对以往数据的记忆功能。下图所示,输入为input和一个状态Hidden0,输出为output和Hidden1.
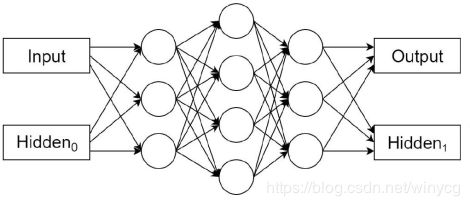
一般地,对输入到RNN进行处理的第 t t t个数据,也就是第 t t t时刻,输出的隐藏状态可以表示为 h ( t ) = f ( h ( t − 1 ) , x ( t ) ; θ ) h^{(t)}=f(h^{(t-1)},x^{(t)};\theta) h(t)=f(h(t−1),x(t);θ)

在RNN对序列数据进行处理时,采用参数共享机制,即权重是相同的。RNN有很多变体,上述的是最简单的一种形式,中间也可以输入 y ( t ) y^{(t)} y(t)。标准RNN如下:

对时刻 t t t,更新的方程为:
h t = tanh ( w i h x t + b i h + w h h h t − 1 + b h h ) h_{t}=\tanh(w_{ih}x_{t}+b_{ih}+w_{hh}h_{t-1}+b_{hh}) ht=tanh(wihxt+bih+whhht−1+bhh)
在实际中使用nn.RNN()模块即可实现标准RNN的调用,下面通过讲解函数中的参数来具体讲解RNN的实用。nn.RNA有如下参数:
- input_size:输入 x x x的特征数量
- hidden_size:隐藏状态 h h h的特征数量
- num_layers:网络层数,默认为1层。若2层,两个RNN单元进行堆叠,第2个RNN单元将第1个RNN单元的 h h h作为输入。
- nonlinearity:实用tanh或ReLU,默认是tanh
- bias:False代表不使用偏置 b i h b_{ih} bih和 b h h b_{hh} bhh,默认为True。
- batch_first:决定输入数据的维度顺序。默认输入是(seq,batch,feature),分别是RNN序列长度,批量数,特征维度。True表示(batch,seq,feature).
- dropout:接收一个0~1的数值,会在网络除最后一层之外的其他输出层加上dropout层,默认为0
- bidirectional:如果是True,表示双向的RNN。
维度流程详解:
RNN接受一个序列输入 x t x_{t} xtwith维度(seq,batch,feature)和记忆输入 h 0 h_{0} h0with维度(num_layers*num_directions,batch,hidden),num_layers表示RNN单元堆叠的层数,num_directions为1(单向RNN)和2(双向RNN),双向RNN就是从左向右计算一次之后再从右向左计算一次,hidden就是输出维度。网络输出为output和 h n h_{n} hn。output表示每个时刻网络最后一层的输出,维度是(seq,batch,hidden*num_directions),即将双向的特征拼接起来。 h n h_{n} hn是最后时刻所有堆叠的记忆单元的所有输出,维度为(num_layers*num_directions, batch,hidden)
>>> import torch.nn as nn
>>> rnn = nn.RNN(10, 20, 2)
>>> input = torch.randn(5, 3, 10)
>>> h0 = torch.randn(2, 3, 20) # h0不初始化则全部为0
>>> output, hn = rnn(input, h0)
建立了一个堆叠了2层的RNN,可通过如下的属性获得权重和偏置参数:
- RNN.weight_ih_l[k]: 表示第 k k k层的input-hidden权重。如果 k = 0 k=0 k=0,表示第0层维度为(hidden_size,input_size),其他层的维度为(hidden_size,num_directions*hidden_size),接收第 k − 1 k-1 k−1层传来的hidden特征。
- RNN.weight_hh_l[k]: 表示第 k k k层的hidden-hidden权重,维度是(hidden_size,hidden_size),接收第 t − 1 t-1 t−1时刻第 k k k层的hidden特征。
- RNN.bias_ih_l[k]: 表示第 k k k层的input-hidden的偏置,维度为(hidden_size)
- RNN.bias_hh_l[k]: 表示第 k k k层的hidden-hidden的偏置,维度为(hidden_size)
>>> rnn.weight_ih_l0.size()
torch.Size([20, 10])
>>> rnn.weight_ih_l1.size()
torch.Size([20, 20])
>>> rnn.weight_hh_l0.size()
torch.Size([20, 20])
>>> rnn.weight_hh_l1.size()
torch.Size([20, 20])
如果误差为负对数似然,则误差为: L ( { x 1 , x 2 , . . . , x T } , { y 1 , y 2 , . . . , y T } ) = ∑ t = 1 T L t = − ∑ t log p m o d e l ( y t ∣ { x 1 , x 2 , . . . , x t } ) L(\{\bm{x}_{1},\bm{x}_{2},...,\bm{x}_{T}\},\{y_{1},y_{2},...,y_{T}\})=\sum_{t=1}^{T}L_{t}\\ =-\sum_{t}\log{p_{model}(y_{t}|\{\bm{x}_{1},\bm{x}_{2},...,\bm{x}_{t}\})} L({x1,x2,...,xT},{y1,y2,...,yT})=t=1∑TLt=−t∑logpmodel(yt∣{x1,x2,...,xt})
RNN的缺点:
根据前面的介绍可以了解RNN对以往数据的具有记忆性,但是存在的问题就是具有遗忘性,总是更加清楚地记得最近处理的记忆而遗忘之前发生的事情,只能很好地解决短时依赖的问题。因为梯度在反向传播的时候, 初始阶段的数据产生的梯度会由于指数级的相乘而很小。