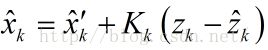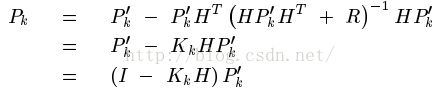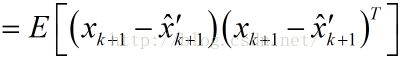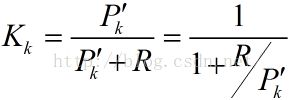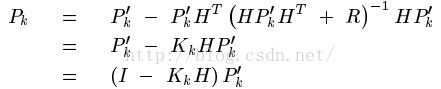卡尔曼算法笔记---思想和实际应用物理含义的理解
此片blog的目的是理解卡尔曼算法的思想和实际应用的物理含义,想法很好,却只能理解冰山一角,先记下这一角
另本blog参考卡尔曼滤波 -- 从推导到应用和徐亦达卡尔曼推导视频
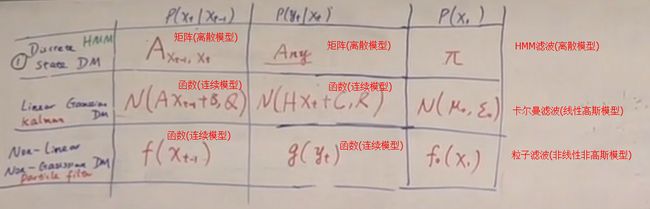
首先认识卡尔曼算法在数学领域是什么位置:处理线性高斯模型的算法
然后认识卡尔曼算法的思想:
一片绿油油的草地上有一条曲折的小径,通向一棵大树.一个要求被提出:从起点沿着小径走到树下.
“很简单.” A说,于是他丝毫不差地沿着小径走到了树下.
现在,难度被增加了:蒙上眼。
“也不难,我当过特种兵。” B说,于是他歪歪扭扭地走到了树旁。“唉,好久不练,生疏了。”(只凭自己的预测能力)
“看我的,我有 DIY的 GPS!” C说,于是他像个醉汉似地歪歪扭扭的走到了树旁。“唉,这个 GPS没做好,漂移太大。”(只依靠外界有很大噪声的测量)
“我来试试。”旁边一也当过特种兵的拿过 GPS,蒙上眼,居然沿着小径很顺滑的走到了树下。(自己能预测+测量结果的反馈)
“这么厉害!你是什么人?”
“卡尔曼 ! ”
“卡尔曼?!你就是卡尔曼?”众人大吃一惊。
“我是说这个 GPS卡而慢。”
也就是说,预测值有高斯噪声,测量值也有高斯噪声,这2个噪声相互独立,单独的利用任何一个都不能很好的得到真实值,所以在2者之间有个信赖度的问题,应该相信谁更多些,这也就是卡尔曼算法的核心,这个信赖度就是卡尔曼增益,卡尔曼增益通过测量值和真实值之间的协方差最小时确定的,由此求这个协方差偏导为0时的系数,这个系数就是卡尔曼增益,这样就能很好的融合预测值和测量值。并且推导卡尔曼增益的时候,发现协方差是可以递归的,由此只要刚开始指定初始协方差就可以源源不断的求出卡尔曼增益和新的协方差,从而不断的跟新真实值。
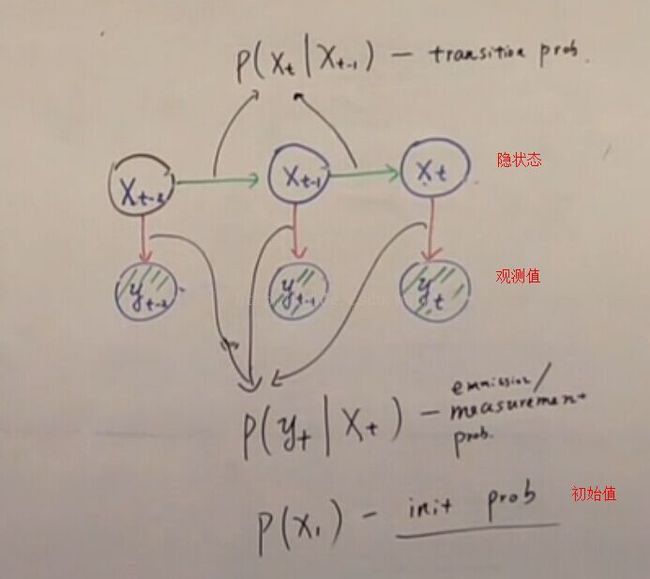
接着是普及数学卡尔曼知识(推导卡尔曼运算过程)
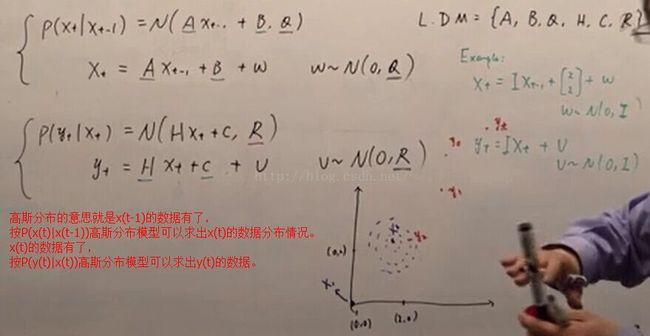
动态模型:最后是实际应用:
1.为了方便表达,把几个公式用矩阵表达式表达
2.估计过程:
(1) 上一时刻状态推导这一时刻状态线性系统的状态。 差分方程为,其中x是系统的状态向量,大小为n*1列。A为转换矩阵,大小为n*n。u为系统输入,大小为k*1。B是将输入转换为状态的矩阵,大小为n*k。随机变量w为系统噪声。注意这些矩阵的大小,它们与你实际编程密切相关。
(2)测量值当然是由系统状态变量映射出来的,方程形式如下:
注意Z是测量值,大小为m*1(不是n*1,也不是1*1,后面将说明),H也是状态变量到测量的转换矩阵。大小为m*n。随机变量v是测量噪声。
同时对于匀加速模型,假设下车是匀加速远离我们,我们站在原点用超声波仪器测量小车离我们的距离。
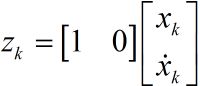
也就是测量值直接等于位移。可能又会问,为什么不直接用测量值呢?测量值噪声太大了,根本不能直接用它来进行计算。试想一个本来是朝着一个方向做匀加速运动的小车,你测出来的位移确是前后移动(噪声影响),只根据测量的结果,你就以为车子一会往前开一会往后开。
对于状态方程中的系统噪声w和测量噪声v,假设服从如下多元高斯分布,并且w,v是相互独立的。其中Q,R为噪声变量的协方差矩阵。
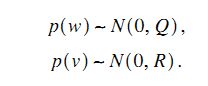
看到这里自然要提个问题,为什么噪声模型就得服从高斯分布呢?个人觉得卡尔曼是在线性高斯的环境下建立的模型,也就是说这个推导有些公式或者定理只能适用于高斯分布这个条件,具体的话,个人只记得如果刚开始协方差满足高斯,递推下去,之后的协方差都满足高斯。
对于小车匀加速运动的的模型,假设系统的噪声向量只存在速度分量上,且速度噪声的方差是一个常量0.01,位移分量上的系统噪声为0。测量值只有位移,它的协方差矩阵大小是1*1,就是测量噪声的方差本身。
那么:
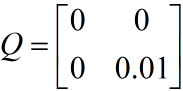
Q中,叠加在速度上系统噪声方差为0.01,位移上的为0,它们间协方差为0,即噪声间没有关联。
(3)噪声(偏差)是如何处理的。貌似有了这个模型就能完全估计系统状态了,速度能计算出,位移也能计算出(这个模型下面的图片有介绍)。那还要卡尔曼干嘛,问题是很多实际系统复杂到根本就建不了模。并且,即使你建立了较为准确的模型,只要你在某一步有误差,由递推公式,很可能不断将你的误差放大A倍(A就是那个状态转换矩阵),以至于最后得到的估计结果完全不能用了。回到最开始的那个笑话,如果那个完全凭预测的特种兵在某一步偏离了正确的路径,当他站在错误的路径上(而他自己以为是正确的)做下一步预测时,肯定走的路径也会错了,到最后越走越偏。
既然如此,我们就引进反馈。从概率论贝叶斯模型的观点来看前面预测的结果就是先验,测量出的结果就是后验。
(4) 如何引入反馈。 理论预测(先验)有了,测量值(后验)也有了,那怎么根据这两者得到最优的估计值呢?首先想到的就是加权,或者称之为反馈。 我们认定其中,![]() 称之为残差,也就是预测的和你实际测量值之间的差距。如果这项等于0,说明预测和测量出的完全吻合。
称之为残差,也就是预测的和你实际测量值之间的差距。如果这项等于0,说明预测和测量出的完全吻合。
(5)卡尔曼的核心:求取卡尔曼增益(也就是加权)。这个里面涉及方差或者协方差,方差好比误差的平方和,目的是求和真实值最小的方差的加权(个人理解)。
友情提示:以下看不懂可以结合上面数学推导理解
先看估计值和真实值间误差的协方差矩阵,提醒一下协方差矩阵的对角线元素就是方差,求这个协方差矩阵,就是为了利用他的对角线元素的和计算得到均方差.
这里请注意ek是向量,它由各个系统状态变量的误差组成。如匀加速运动模型里,ek便是由位移误差和速度误差,他们组成的协方差矩阵。表示如下:
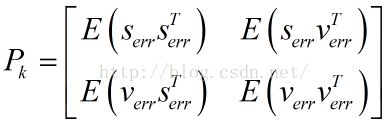
其中,Serr代表位移误差,Verr代表速度误差,对角线上就是各自的方差。
把前面得到的估计值代入这里能够化简得:
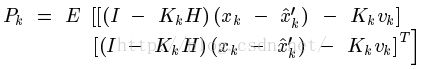 (
这里中间是乘
) (1)
式
(
这里中间是乘
) (1)
式
同理,能够得到预测值和真实值之间误差的协方差矩阵:

注意到系统状态x变量和测量噪声之间是相互独立的。于是展开(1)式可得:

最后得到:
继续展开:
接下来最小均方差开始正式登场了,回忆之前提到的,协方差矩阵的对角线元素就是方差。这样一来,把矩阵P的对角线元素求和,用字母T来表示这种算子,他的学名叫矩阵的迹。
最小均方差就是使得上式最小,对未知量K求导,令导函数等于0,就能找到K的值。

![]()
注意这个计算式K,转换矩阵H式常数,测量噪声协方差R也是常数。因此K的大小将与预测值的误差协方差有关。不妨进一步假设,上面式子中的矩阵维数都是1*1大小的,并假设H=1,![]() 不等于0。那么K可以写成如下:
不等于0。那么K可以写成如下: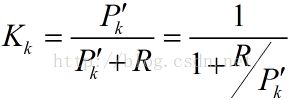
所以![]() 越大,那么K就越大,权重将更加重视反馈,如果
越大,那么K就越大,权重将更加重视反馈,如果![]() 等于0,也就是预测值和真实值相等,那么K=0,估计值就等于预测值(先验)。(完全满足之前说的:方差好比误差的平方和,目的是求和真实值最小的方差的加权。也就是说预测值和真实值的方差越大,卡尔曼增益越大,越相信测量值;预测值和真实值的方差越小,卡尔曼增益越小,越相信预测值)
等于0,也就是预测值和真实值相等,那么K=0,估计值就等于预测值(先验)。(完全满足之前说的:方差好比误差的平方和,目的是求和真实值最小的方差的加权。也就是说预测值和真实值的方差越大,卡尔曼增益越大,越相信测量值;预测值和真实值的方差越小,卡尔曼增益越小,越相信预测值)
将计算出的这个K反代入Pk中,就能简化Pk,估计协方差矩阵Pk的:
因此递推公式中每一步的K就计算出来了,同时每一步的估计协方差也能计算出来。但K的公式中好像又多了一个我们还未曾计算出来的东西![]() ,他称之为预测值和真实值之间误差的协方差矩阵。它的递推计算如下:
,他称之为预测值和真实值之间误差的协方差矩阵。它的递推计算如下:
请先注意到预测值的递推形式是:
由于系统状态变量和噪声之间是独立,故可以写成:
由此也得到了![]() 的递推公式。因此我们只需设定最初的
的递推公式。因此我们只需设定最初的![]() ,就能不断递推下去。
,就能不断递推下去。
这个递推的过程是:我们需要卡尔曼增益k,作为最优加权值,用于估计真实值
“死”步骤

再来点lpe的程序分析:那就以气压和光流为例
程序就是按上面介绍的思路来写的:先用物理模型推测下一刻的状态,再用传感器得到带有噪声的位置速度等信息,最后通过算最小协方差时的卡尔曼增益,并加权得到最优解。
void BlockLocalPositionEstimator::predict()
{
// if can't update anything, don't propagate
// state or covariance
if (!_canEstimateXY && !_canEstimateZ) { return; }
if (_integrate.get() && _sub_att.get().R_valid) {
Matrix3f R_att(_sub_att.get().R);
Vector3f a(_sub_sensor.get().accelerometer_m_s2);
_u = R_att * a;
_u(U_az) += 9.81f; // add g
} else {
_u = Vector3f(0, 0, 0);
}
// dynamics matrix
Matrix A; // state dynamics matrix
A.setZero();
// derivative of position is velocity
A(X_x, X_vx) = 1;
A(X_y, X_vy) = 1;
A(X_z, X_vz) = 1;
// derivative of velocity is accelerometer acceleration
// (in input matrix) - bias (in body frame)
Matrix3f R_att(_sub_att.get().R);
A(X_vx, X_bx) = -R_att(0, 0);
A(X_vx, X_by) = -R_att(0, 1);
A(X_vx, X_bz) = -R_att(0, 2);
A(X_vy, X_bx) = -R_att(1, 0);
A(X_vy, X_by) = -R_att(1, 1);
A(X_vy, X_bz) = -R_att(1, 2);
A(X_vz, X_bx) = -R_att(2, 0);
A(X_vz, X_by) = -R_att(2, 1);
A(X_vz, X_bz) = -R_att(2, 2);
// input matrix
Matrix B; // input matrix
B.setZero();
B(X_vx, U_ax) = 1;
B(X_vy, U_ay) = 1;
B(X_vz, U_az) = 1;
// input noise covariance matrix
Matrix R;
R.setZero();
R(U_ax, U_ax) = _accel_xy_stddev.get() * _accel_xy_stddev.get();
R(U_ay, U_ay) = _accel_xy_stddev.get() * _accel_xy_stddev.get();
R(U_az, U_az) = _accel_z_stddev.get() * _accel_z_stddev.get();
// process noise power matrix
Matrix Q;
Q.setZero();
float pn_p_sq = _pn_p_noise_density.get() * _pn_p_noise_density.get();
float pn_v_sq = _pn_v_noise_density.get() * _pn_v_noise_density.get();
Q(X_x, X_x) = pn_p_sq;
Q(X_y, X_y) = pn_p_sq;
Q(X_z, X_z) = pn_p_sq;
Q(X_vx, X_vx) = pn_v_sq;
Q(X_vy, X_vy) = pn_v_sq;
Q(X_vz, X_vz) = pn_v_sq;
// technically, the noise is in the body frame,
// but the components are all the same, so
// ignoring for now
float pn_b_sq = _pn_b_noise_density.get() * _pn_b_noise_density.get();
Q(X_bx, X_bx) = pn_b_sq;
Q(X_by, X_by) = pn_b_sq;
Q(X_bz, X_bz) = pn_b_sq;
// terrain random walk noise
float pn_t_sq = _pn_t_noise_density.get() * _pn_t_noise_density.get();
Q(X_tz, X_tz) = pn_t_sq;
// continuous time kalman filter prediction
Vector dx = (A * _x + B * _u) * getDt();
// only predict for components we have
// valid measurements for
if (!_canEstimateXY) {
dx(X_x) = 0;
dx(X_y) = 0;
dx(X_vx) = 0;
dx(X_vy) = 0;
}
if (!_canEstimateZ) {
dx(X_z) = 0;
dx(X_vz) = 0;
}
// propagate
_x += dx;
_P += (A * _P + _P * A.transpose() +
B * R * B.transpose() + Q) * getDt();
} void BlockLocalPositionEstimator::baroCorrect()
{
// measure
Vector y;
if (baroMeasure(y) != OK) { return; }
// subtract baro home alt
y -= _baroAltHome;
// baro measurement matrix
Matrix C;
C.setZero();
C(Y_baro_z, X_z) = -1; // measured altitude, negative down dir.
Matrix R;
R.setZero();
R(0, 0) = _baro_stddev.get() * _baro_stddev.get();
// residual
Matrix S_I =
inv((C * _P * C.transpose()) + R);
Vector r = y - (C * _x);
// fault detection
float beta = (r.transpose() * (S_I * r))(0, 0);
if (beta > BETA_TABLE[n_y_baro]) {
if (_baroFault < FAULT_MINOR) {
//mavlink_and_console_log_info(&mavlink_log_pub, "[lpe] baro fault, r %5.2f m, beta %5.2f",
//double(r(0)), double(beta));
_baroFault = FAULT_MINOR;
}
} else if (_baroFault) {
_baroFault = FAULT_NONE;
//mavlink_and_console_log_info(&mavlink_log_pub, "[lpe] baro OK");
}
// kalman filter correction if no fault
if (_baroFault < fault_lvl_disable) {
Matrix K = _P * C.transpose() * S_I;
Vector dx = K * r;
if (!_canEstimateXY) {
dx(X_x) = 0;
dx(X_y) = 0;
dx(X_vx) = 0;
dx(X_vy) = 0;
}
_x += dx;
_P -= K * C * _P;
}
} 这段的代码也很好理解,倒着看。
代码的目的是矫正高度,怎么矫正?predict()函数最后面_x += dx;这个dx就是通过模型推导的,而baroCorrect()函数_x += dx;这里的dx = K * r;其中K是卡尔曼增益K = _P * C.transpose() * S_I;r是测量值和预测值的误差,r = y - (C * _x);这里y是测量值,C是转换矩阵将预测矩阵转换成测量矩阵,_x就是预测值。这里的核心就是K的求法,这里涉及了协方差和一些运算,这个是可以从程序一眼看出来的,具体公式和求法没研究的很清楚。
相同的,看光流,求法是一样的,只是测量矩阵不一样了,噪声等“个性化”东西不一样,处理过程是一样的。
如果您觉得此文对您的发展有用,请随意打赏。
您的鼓励将是笔者书写高质量文章的最大动力^_^!!