耶鲁大学博弈论公开课全24集第19集笔记:招商引资和战略投资
耶鲁大学博弈论公开课全24集第19集笔记:招商引资和战略投资
- 1. 视频地址
- 2. 本集思维导图
- 3. 上集回顾
- 4. 案例一:“别搞砸了”
- 4.1 问题分析
- 4.2 冗余的指示告诉我们如何行动
- 4.3 结论
- 5. 案例二:介绍人博弈
- 5.1 问题描述
- 5.2 纯策略情况分析
- 5.3 混合策略情况分析
- 5.4 结论
- 6.案例三:投资策略小型案例分析
- 6.1 问题描述
- 6.2 问题分析
- 6.2.1 会计师的答案
- 6.2.2 经济学家的答案
- 6.2.3 博弈论的答案
- 6.3 结论
1. 视频地址
Bilibili耶鲁大学博弈论公开课全24集
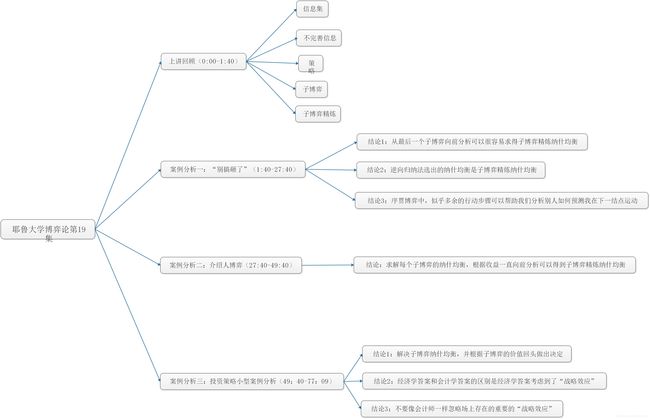
2. 本集思维导图
3. 上集回顾
- 信息集:用于帮助对不完善信息进行建模。
- 不完善信息:使我们在同一个博弈中获知同时行为(simultaneous movement)和序贯行为(sequential movement)的方法。
- 策略:对于每个参与人来说,策略在每一个信息集中给予他们指示。
- 子博弈:简单来说就是博弈中的博弈。
- 子博弈精炼纳什均衡:指导参与人在每个子博弈中都达到纳什均衡。是整个博弈的纳什均衡,在每个子博弈中也仍然存在纳什均衡。
4. 案例一:“别搞砸了”
4.1 问题分析
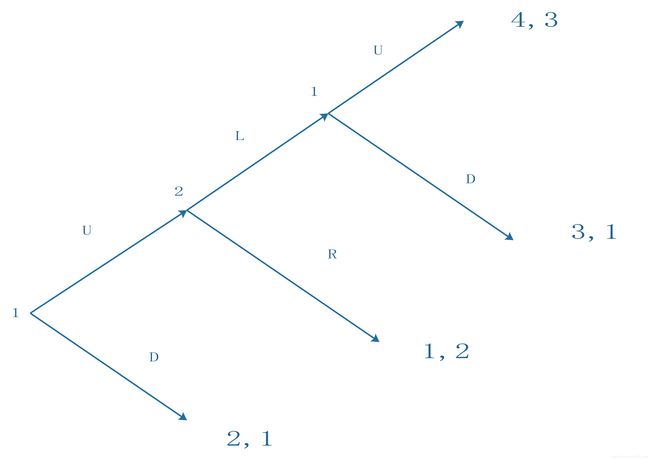
首先采用逆向归纳法(Backward Induction)分析,可以得到参与人做出的选择是(U,L,U)。但是在课堂投票中出现了参与人1选择一开始就退出(选择D)的情况和参与人2在参与人1选择U后选择R的情况。
第一种情况来源于参与人1担心参与人2会在第二步搞砸(不去选择L而去选择R)导致自己本可以获得4个单位的收益最后只能获得1个单位。所以参与人1更愿意先退出获得2个单位的收益。
第二种情况来源于参与人2担心参与人1会在第三步搞砸(不去选择U而去选择D)导致自己本可以获得3个单位的收益最后只能获得1个单位。所以参与人2更愿意选择R获得2个单位的收益。
所以需要参与人1相信参与人2不会搞砸,参与人2相信参与人1不会搞砸,参与人1相信参与人2相信参与人1不会搞砸…(类似序贯理性)才能使得(U,L,U)成立。
使用4*2矩阵表示该序贯博弈:
| 参与人1/参与人2 | L | R |
|---|---|---|
| UU | 4,3 | 1,2 |
| UD | 3,1 | 1,2 |
| DU | 2,1 | 2,1 |
| DD | 2,1 | 2,1 |
可以找到三个纳什均衡,分别为(U,L,U),(D,R,U),(D,R,D)。第一个显然是我们通过逆向归纳法得到的,而后俩个则并不适合逆向归纳法(符合之前我们分析的害怕把对方把事情搞砸的想法)我们需要去找到子博弈精炼纳什均衡。
4.2 冗余的指示告诉我们如何行动
在最后一个结点形成的子博弈中,纳什均衡是选择U,得到(4,3)。(U,L,U)和(D,R,U)指示我们去选择U,而(D,R,D)中指示我们选择D,不能构成子博弈的纳什均衡,故是冗余指示,所以可以排除(D,R,D)。
在倒数第二个结点形成的子博弈中,博弈矩阵如下,存在两个纯策略纳什均衡(U,L),(D,R):
| 参与人1/参与人2 | L | R |
|---|---|---|
| U | 4,3 | 1,2 |
| D | 3,1 | 1,2 |
(U,L,U)的后两步符合(U,L),指示正确;(D,R,U)的后两步不符合(U,L)和(D,R),即指示错误;(D,R,D)的后两步符合(D,R),指示正确(虽然(D,R,D)已经被排除了,但是它正确指示了此时形成的纳什均衡)。因此我们排除(D,R,U)。
再考虑原博弈,我们已经排除了(D,R,U)和(D,R,D),唯一剩下的(U,L,U)是子博弈精炼纳什均衡,而且符合我们逆向归纳法的结果。
4.3 结论
①子博弈精炼纳什均衡很容易求出,只需要考虑子博弈,是否使得每个子博弈都达到纳什均衡,只需从后面往前开始分析,从最后一个子博弈到主博弈。
②子博弈精炼纳什均衡和逆向归纳法结果一样,逆向归纳法选出的纳什均衡是子博弈精炼纳什均衡。
③行动似乎多余的步骤可以帮助我们分析别人怎么预测我在下一节点运动的。,在我终止前我会考虑你对我的行为是怎么想的。
5. 案例二:介绍人博弈
5.1 问题描述
参与人1会选择是否撮合一对男女(参与人2和参与人3),若不撮合则无任何效用发生,若撮合则男女进行“性别之战(Battle of sexes)”,如果他们见面(协调成功)则三者皆大欢喜,如果男女未能做出相同的选择,则撮合人因没能成功撮合,效用为-1。
5.2 纯策略情况分析
首先从最后一个子博弈(即参与人2所处结点,因为3处在同一信息集内那里不能构成子博弈)进行倒推。我们可以得到“性别之战”的博弈矩阵(不妨也在收益里加上参与人1的收益):
| 参与人2/参与人3 | G | S |
|---|---|---|
| G | 1,2,1 | -1,0,0 |
| S | -1,0,0 | 1,1,2 |
我们可以得到两个纯策略纳什均衡(G,G)和(S,S)。对于参与人1来说此时只关注参与人2和参与人3是否能见面,很幸运的是,此时的两个纯策略纳什均衡都可以给他带来收益。
考虑原博弈,此时参与人1将会在不撮合的0收益和撮合而产生的1收益(因为他知道另外两人会形成纳什均衡)中选择,他会选择撮合。故纯策略情况下,子博弈精炼纳什均衡有两个:(撮合,G,G)和(撮合,S,S)。
5.3 混合策略情况分析
在参与人2和参与人3选择混合策略的情况下,参与人1是否会选择撮合参与人2和参与人3?
根据我方使用混合策略必然使得对方使用任何策略都没有区别,我们可以得出双方混合两种策略的概率:
| 参与人2/参与人3 | 1 3 \frac{1}{3} 31G | 2 3 \frac{2}{3} 32S |
|---|---|---|
| 2 3 \frac{2}{3} 32G | 2,1 | 0,0 |
| 1 3 \frac{1}{3} 31S | 0,0 | 1,2 |
此时两人协调成功的概率为:
2 3 × 1 3 + 1 3 × 2 3 = 4 9 \frac{2}{3}\times \frac{1}{3}+\frac{1}{3}\times \frac{2}{3}=\frac{4}{9} 32×31+31×32=94
而不成功的概率则为5/9。故此时参与人1的期望收益为:
4 9 × 1 + 5 9 × ( − 1 ) = − 1 9 \frac{4}{9}\times 1+\frac{5}{9}\times \left( -1 \right) =-\frac{1}{9} 94×1+95×(−1)=−91
故还存在一个混合策略纳什均衡:(不撮合,(2/3选择G,1/3选择S),(1/3选择S,2/3选择G))
5.4 结论
求解子博弈精炼纳什均衡,只需要保持头脑清醒,求每个子博弈的纳什均衡,通过收益向前分析,分析博弈树上一节点的最优策略是什么。
6.案例三:投资策略小型案例分析
6.1 问题描述
A、B两家化肥生产公司处于古诺竞争中,逆需求曲线为:
P = 2 − 1 3 ( q a + q b ) P=2-\frac{1}{3}\left( q_a+q_b \right) P=2−31(qa+qb)
其中P为价格,qa和qb分别为两家公司的产量。边际成本为每吨1美元(c=1)。
根据古诺模型的分析,我们可以很容易求出每家公司的古诺产量(单位百万吨),市场的价格水平(单位美元/吨)和每家公司的收益(单位百万美元):
q a = q b = 1 , P = 1.33 , π a = π b = 0.33 q_a=q_b=1,\ P=1.33,\ \pi _a=\pi _b=0.33 qa=qb=1, P=1.33, πa=πb=0.33
A公司需要选择是否租用一台新机器,新机器有三个特点:
- 该机器只为A公司工作
- 该机器每年租金为0.7百万美元(70w美元)
- 可以把A公司的生产成本降低为0.5美元/吨
问:A公司是否该租用该机器?
6.2 问题分析
6.2.1 会计师的答案
因为我的产量时1百万吨,降低成本给我增多0.5百万美元的利润,租用机器需要0.7百万美元,因此我不应该租用机器。(错误)
因为会计师错误地假设每年产量还是1百万吨(B公司会改变他的产量)
6.2.2 经济学家的答案
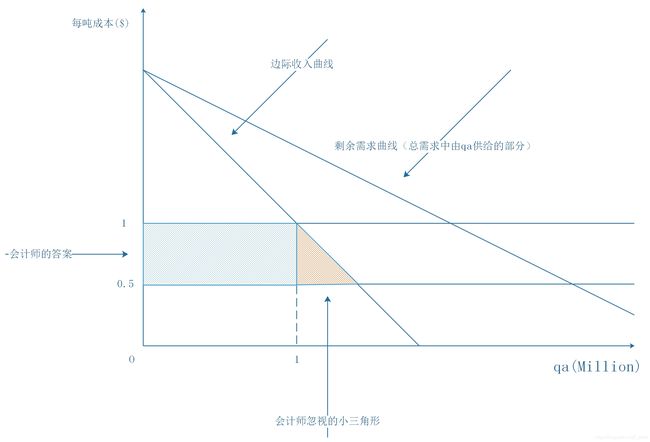
根据边际成本等于边际收益,我们可以求出降低成本带来的利润,会计师只关注了那个无聊的矩形,而实际上降低成本带来的利润还包括我的产量增加而带来的小三角形,可以计算出总的利润为矩形面积+三角形面积(边际收入曲线的斜率为-2/3):
总利润 = ( 1 − 0.5 ) × 1 + ( 1 − 0.5 ) × 3 4 × 1 2 = 0.6875 \text{总利润}=\left( 1-0.5 \right) \times 1+\left( 1-0.5 \right) \times \frac{3}{4}\times \frac{1}{2}=0.6875 总利润=(1−0.5)×1+(1−0.5)×43×21=0.6875
因为0.6875<0.7,故仍然不应该租用机器(错误)
不幸的是,这个答案仍然是错误的。
6.2.3 博弈论的答案
原古诺模型两企业的利润分别为:
π a = ( 2 − 1 3 ( q a + q b ) − 1 ) q a π b = ( 2 − 1 3 ( q a + q b ) − 1 ) q b \pi _a=\left( 2-\frac{1}{3}\left( q_a+q_b \right) -1 \right) q_a \space\space\space\space\space\space \pi _b=\left( 2-\frac{1}{3}\left( q_a+q_b \right) -1 \right) q_b πa=(2−31(qa+qb)−1)qa πb=(2−31(qa+qb)−1)qb
由一阶条件得到的每个企业的最优反应曲线(Best Response Curve)为:
q b = 3 − 2 q a q a = 3 − 2 q b q_b=3-2q_a \space\space\space\space\space\space\space\space\space q_a=3-2q_b qb=3−2qa qa=3−2qb
而如果租用机器,两企业的利润分别为:
π a = ( 2 − 1 3 ( q a + q b ) − 0.5 ) q a π b = ( 2 − 1 3 ( q a + q b ) − 1 ) q b \pi _a=\left( 2-\frac{1}{3}\left( q_a+q_b \right) -0.5 \right) q_a \space\space\space\space\space\space \pi _b=\left( 2-\frac{1}{3}\left( q_a+q_b \right) -1 \right) q_b πa=(2−31(qa+qb)−0.5)qa πb=(2−31(qa+qb)−1)qb
一阶条件得到租用机器后每个企业的最优反应曲线:
q b = 4.5 − 2 q a q a = 3 − 2 q b q_b=4.5-2q_a \space\space\space\space\space\space\space\space\space q_a=3-2q_b qb=4.5−2qa qa=3−2qb
即相当于A企业的最优反应曲线右移了:
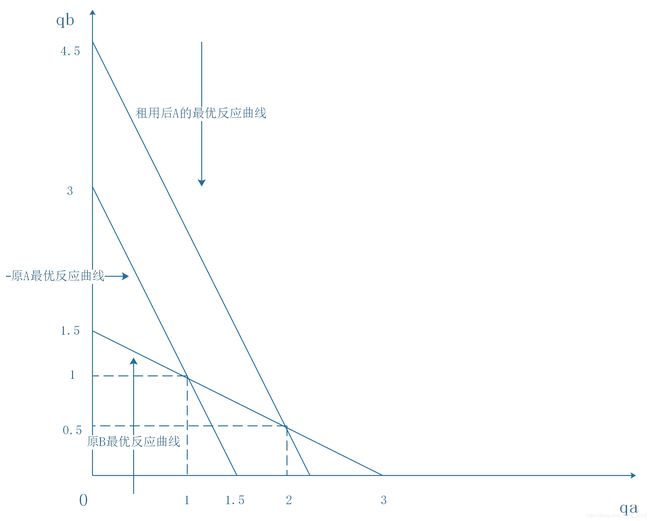
租用机器后A将会很高兴,因为此时B的产量将会减少(所谓 “战略替代”),此时自己可以生产更多的化肥。新的A的最优反应曲线和B的最优反应曲线的交点为新的古诺均衡(非对称古诺模型),可以计算出A企业此时的利润为:
π a = ( 2 − 1 3 ( 2 + 0.5 ) − 0.5 ) × 2 = 1.33333 \pi _a=\left( 2-\frac{1}{3}\left( 2+0.5 \right) -0.5 \right) \times 2=1.33333 πa=(2−31(2+0.5)−0.5)×2=1.33333
比不租用机器时的利润多了1百万元,大于租用机器的0.7百万元,因此我们应该选择租用机器。
更进一步来说,我们可以把这个过程看做一个序贯博弈,首节点为A选择租用机器或是不租用机器,若不租用则进入原古诺模型,租用则进入新的古诺模型。我们要求整个博弈的子博弈精炼纳什均衡的话,跟前两个案例类似,我们先分析子博弈(也就是租用机器后产生的新的古诺模型),找到这个子博弈的纳什均衡(也就是新的古诺均衡),将这个均衡的收益和原来不租用机器的古诺均衡的收益进行对比,然后再做出是否租用机器的决定。
6.3 结论
- 分析这种问题要先分析子博弈,解决子博弈的纳什均衡,从子博弈的价值出发回头做决定。在本案例的博弈树中,一边是对称古诺模型,另一边是非对称的新古诺模型。
- 经济学答案和会计学答案的区别,是经济学答案考虑到了战略效应。(其他参与人改变其行为的影响)。我们参与策略的时候要考虑战略效应(其他人也会因我们的行为改变而改变行为),才能有利可图。
如:给美国设计税收政策,如果观察人们都在做什么,然后带入新的税收参数,像会计师一样计算政府收入是多少,这是错误的。因为改变了税法,人们也会相应地行动,需要考虑战略效应。
如:给耶鲁大学设计新的课程制度,改变了课程的现有规章制度。在新的规章制度下如果观察学生过去如何表现,在新的课程制度下他们又会如何如何做,忽略了学生会对改变课程规章制度这一行为做出反应。
- 别像会计师一样,因为这样无聊而且会毁了你的约会,另外这样你会忽略场上存在的重要的战略效应。