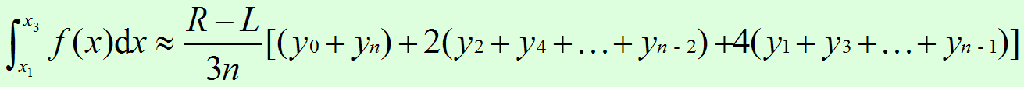simpson积分公式
看了Simpson积分公式,惊讶于积分方法在几何问题中竟如此强大!
比如几何中的求面积、体积问题,可以用积分的方法,在某个方向上用扫描线或扫描面切过图形,求被覆盖的长度或面积,然后进行积分。
对于这类问题,如果能直接求出面积、体积,或者能列出覆盖长度(面积)关于扫描线(面)的位置的函数,然后手算积分,那当然是再好不过了。但是,如果直接用解析法、公式法比较费时费力,思考难度大,而题目对精度的要求不高(比如精确到0.01,0.001),数据规模不大,可以考虑用积分的方法。
用程序进行积分,一般的方法是矩形(梯形)切割法,但精度比较差。这里用Simpson积分公式,原理是用二次曲线逼近原函数,精度比矩形切割要好。
引理:在平面直角坐标系中,由任意三点(x1, y1), (x2, y2), (x3, y3)(x1<x2<x3,x2 = (x1 + x3)/2)确定的抛物线y= f(x)在[x1, x3]的定积分为
证明不难,暴力拆开即可。
设f(x) = ax2 + bx + c,于是
左边 = (ax33/3 + bx32/2 + cx3) – (ax13/3 + bx12/2 + cx3)
=1/6 × [ 2a(x33 – x13) + 3b(x32 – x12) + 6c(x3 – x1) ]
=1/6 × (x3 – x1) ×[ 2a(x32 + x3x1 + x12) + 2b(x3 + x1) + 6c ]
=1/6 (x3 – x1)
×[ (ax32 + bx3 + c) + (ax12 + bx1 + c) + a(x3+x1)2 + 2b(x3+x1) + 4c ]
=1/6 (x3 – x1) [ y1 + y3 + a(x3+x1)2 + 2b(x3+x1) + 4c ]
注意到x2 = (x1 + x3)/2,所以
左边 = 1/6 (x3 – x1) [ y1 + y3 + 4ax22 + 4bx2+ 4c ]
= 1/6 (x3 – x1) [ y1 + y3 + 4y2 ] = 右边
那么,如果我们把要积分的区域[L, R]划分成n份(n为偶数),份与份之间的分割线的横坐标为x0~xn,其中x0 = L, xn = R,对应的函数值分别为y0~yn,那么,对第0,1,2条分割线;第2,3,4条分割线;第4,5,6条分割线……之间的区域各自进行二次曲线拟合,即应用上面的公式,把结果累加起来,可以得到下面的Simpson积分公式:
(上面的公式中左边的积分号应该是L到R,之前写错了,抱歉)
有时,如果对划分的份数不太确定,可以使用一种叫做“自适应Simpson”的方法。对要积分的区域[L, R]分成两半[L, mid]和[mid, R],如果用二次曲线对(L, mid, R)求出的积分值,和对(L, (L+mid)/2, mid)和(mid, (mid+R)/2, R)分别积分在加起来的值,相差不超过某个精确度,那么就可以停止划分。
(要注意误差的叠加效应,当划分份数比较多时,每一份的误差虽然很小,但叠加在一起可能很大,所以精确度尽量设小)
如果我们能确定被积函数(就是覆盖长度或面积关于扫描位置的函数)是个一次多项式或者二次多项式,但是我们不想把函数式求出来,那也没关系,用上面的方法积分,因为用了二次曲线拟合,答案还是准确的。
要注意的一点是,被积函数在我们想积分的一段上应该是有连续的取值的,就是说,我们积分的扫描线范围[L, R],在[L, R]内不能出现的某条扫描线,它没有穿过任何图形。(这样很有可能L, R, mid都没有穿过图形,求出的答案为0)所以一开始要把有图形的“竖线区”预处理出来。预处理的方法是,每个图形都有一个“被穿过”段,把这些段进行合并就可以了。
Simpson积分方法十分暴力好写。之前某题“多个圆与一个凸多边形的面积并”,用普通的扫描线算法写了250+行,而用积分的方法,只写了130行左右,而且思考难度低,特殊情况少。
附上代码:(此题为SPOJ-CIRU,圆的面积并裸题,自适应Simpson)
#include
#include
#include
#include
#include
usingnamespace std;
#define maxN 1055
#define eps (1e-6)
inlinedouble sqr(double x){return x * x;}
int N;
struct Tcir
{
double Ox, Oy, r;
void read(){scanf("%lf%lf%lf",&Ox,&Oy,&r);}
} cir[maxN];
pair<double,double> itv[maxN];
double f(double x)
{
int tot =0;
for(int i =1; i <= N;++ i)//itv[i] = cir[i].Calc(x);
{
double h = sqr(cir[i].r)- sqr(x - cir[i].Ox);
if(h <0)continue;
h = sqrt( fabs(h));
++ tot;
itv[tot].first = cir[i].Oy - h;
itv[tot].second = cir[i].Oy + h;
}
sort(itv +1, itv + tot +1);
double L =-(1e5), R =-(1e5), res =0;
for(int i =1; i <= tot;++ i)
{
if(itv[i].first > R)
{
res += R - L;
L = R = itv[i].first;
}
if(itv[i].second > R) R = itv[i].second;
}
res += R - L;
return res;
}
double Cnt(double len,double fL,double fmid,double fR)
{
return len *(fL + fR +4* fmid)/6;
}
double Simpson(double L,double mid,double R,double fL,double fmid,double fR,double S)
{
double mid1 =(L + mid)/2;
double fmid1 = f(mid1);
double S1 = Cnt( mid-L, fL, fmid1, fmid );
double mid2 =(mid + R)/2;
double fmid2 = f(mid2);
double S2 = Cnt( R-mid, fmid, fmid2, fR );
if( fabs(S1 + S2 - S)< eps )return S1 + S2;
elsereturn Simpson(L, mid1, mid, fL, fmid1, fmid, S1)
+Simpson(mid, mid2, R, fmid, fmid2, fR, S2);
}
double Simpson(double L,double R)
{
double fL = f(L), fR = f(R), mid =(L + R)/2;
double fmid = f(mid);
double S = Cnt(R-L, fL, fmid, fR);
return Simpson( L, mid, R, fL, fmid, fR, S );
}
pair<double,double> evt[maxN];
int main()
{
freopen("input.txt","r", stdin);
freopen("output.txt","w", stdout);
scanf("%d",&N);
for(int i =1; i <= N;++ i)
{
cir[i].read();
evt[i].first = cir[i].Ox - cir[i].r;
evt[i].second = cir[i].Ox + cir[i].r;
}
sort(evt+1, evt+N+1);
double L =-(1e5), R =-(1e5), ans =0;
for(int i =1; i <= N;++ i)
{
if(evt[i].first > R)
{
ans += Simpson(L, R);
L = R = evt[i].first;
}
if(evt[i].second > R) R = evt[i].second;
}
ans += Simpson(L, R);
printf("%.3lf\n", ans);
return0;
}
精简的核心代码:
template
double simpson(const T &f,double a,double b,int n)
{
const double h = (b-a)/n;
double ans = f(a) + f(b);
for(int i = 1;i < n;i+=2) ans += 4*f(a+i*h);
for(int i = 2;i < n;i += 2) ans += 2*f(a+i*h);
return ans*h/3;
}