【大话数据结构】第五章总结——串

目录

 

1、串的定义

2、串的比较

3、串的抽象数据类型

4、串的存储结构

5、朴素的模式匹配算法

6、KMP模式匹配算法

总结

---

1、串的定义

串（string）是由零个或多个字符组成的有限序列，又名叫字符串

 

串的长度

串中的字符数目n称为串的长度

 

空串

零个字符的串即为空串（null string）

 

空格串

只包含空格的串。其内容是有长度的，而且可以不止一个空格，所以它不算空串

 

子串与主串

串中任意个数的连续字符组成的子序列称为该串的子串，相应地，包含子串的串称为主串

（子串在主串中的位置就是子串的第一个字符在主串中的符号）

 

2、串的比较

事实上，串的比较是通过组成串的字符之间的编码来进行的，而字符的编码指的是字符在对应字符集中的序号

 

串相等

两个串只有它们的长度以及它们各个对应位置的字符都相等时，才算相等

 

串不相等时

给定两个串：s = "a1a2......an", t = "b1b2......bn"，当满足以下条件之一时，s < t

    1、n < m, 且ai = bi (i = 1, 2, ......, n)

    例如当s = "long", t = "longer"，就有s < t。因为t比s多出了两个字母。

    2、存在某个k ≤ min(m, n)，使得ai = bi (i = 1, 2, ......, k - 1)，ak < bk

    例如当s = "longed", t = "longer"，因为前五个字母均相同，而两串第6个字母(k值)，字母d的ASCII码是100，字母r的ASCII码是114，显然d < r，所以s < t

 

3、串的抽象数据类型

对于串的基本操作跟线性表有很大的区别。线性表更关注的是单个元素的操作，比如查找一个元素，插入或删除一个元素，但串中更多的是查找子串位置、得到指定位置子串、替换子串等操作

ADT    串(string)

Data

    串中元素仅由一个字符组成，相邻元素具有前驱和后继关系。

Operation

    StrAssign(T, *chars): 生成一个其值等于字符串常量chars的串T。

   StrCopy(T, S): 串S存在，由串S复制得串T。

   ClearString(S): 串S存在，将串清空。

   StringEmpty(S): 若串S为空，返回true，否则返回false。

   StrLength(S): 返回串S的元素个数，即串的长度。

   StrCompare(S, T): 若S > T，返回值 > 0，若S = T，返回0，若S < T，返回值 < 0。

   Concat(T, S1, S2): 用T返回由S1和S2联接而成的新串。

   SubString(Sub, S, pos, len): 串S存在，1 ≤ pos ≤ StrLength(S)，

                                                 且0 ≤ len ≤ StrLength(S) - pos + 1，用Sub返回

                                                 串S的第pos个字符起长度为len的子串。

   Index(S, T, pos): 串S和T存在，T是非空串，1 ≤ pos ≤ StrLength(S)。

                              若主串S中存在和串T值相同的子串，则返回它在主串S中

                              第pos个字符之后第一次出现的位置，否则返回0。

   Replace(S, T, V): 串S、T和V存在，T是非空串。用V替换主串S中出现的所有与T相等的不重叠的子串。

   StrInsert(S, pos, T): 串S和串T存在，1 ≤ pos ≤ StrLength(S) + 1。

                                    在串S的第pos个字符之前插入串T。

   StrDelete(S, pos, len): 串S存在，1 ≤ pos ≤ StrLength(S) - len + 1。

                                       从串S中删除第pos个字符起长度为len的子串。

endADT

 

操作Index的实现算法

/*T为非空串。若主串S中第pos个字符之后存在与T相等的子串*/
/*则返回第一个这样的子串在S中的位置，否则返回0*/
int Index(String S, String T, int pos){
    int n, m, i;
    String sub;
    if(pos > 0){
        n = StrLength(S);/*得到主串S的长度*/
        m = StrLength(T);/*得到主串T的长度*/
        i = pos;
        while(i <= n - m + 1){
            SubString(sub, S, i, m);/*取主串第i个位置*/
                                    /*长度与T相等子串给sub*/
            if(StrCompare(sub, T) != 0)/*如果两串不相等*/
                ++i;
            else                       /*如果两串相等*/
                return i;              /*则返回i值*/
        }
    }
    return 0;/*若无子串与T相等，返回0*/
}

 

4、串的存储结构

1、串的顺序存储结构

串的顺序存储结构是用一组地址连续的存储单元来存储串中的字符序列的。

按照预定义的大小，为每个定义的串变量分配一个固定长度的存储区。一般是用定长数组来定义。

 

2、串的链式存储结构

对于串的链式存储结构，与线性表是相似的，但由于串结构的特殊性，结构中的每个元素数据是一个字符，如果也简单的应用链表存储串值，一个结点对应一个字符，就会存在很大的空间浪费。

因此，一个结点可以存放一个字符，也可以考虑存放多个字符，最后一个结点若是未被占满时，可以用"#"或其他非串值字符补全，如下图所示：

 

5、朴素的模式匹配算法

串的模式匹配

即子串的定位操作，是串中最重要的操作之一。

 

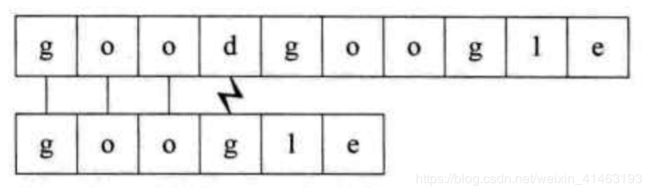
假设要从下面的主串S = "goodgoogle"中，找到T = ”google"这个子串的位置，需要如下步骤：

1、主串S第一位开始，S与T前三个字母都匹配成功，但S第四个字母是d而T的是g。第一位匹配失败。

如下图所示，其中竖直连线表示相等，闪电状弯折连线表示不等。

 

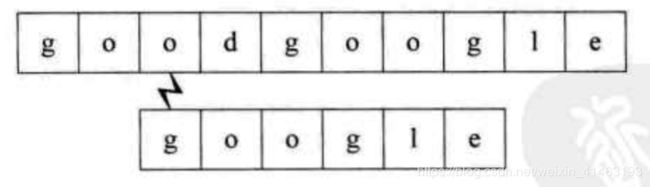
2、主串S第二位开始，主串S首字母是o，要匹配的T首字母是g，匹配失败，如下图所示

 

3、主串S第三位开始，主串S首字母是o，要匹配的T首字母是g，匹配失败，如下图所示

 

4、主串S第四位开始，主串S首字母是d，要匹配的T首字母是g，匹配失败，如下图所示

 

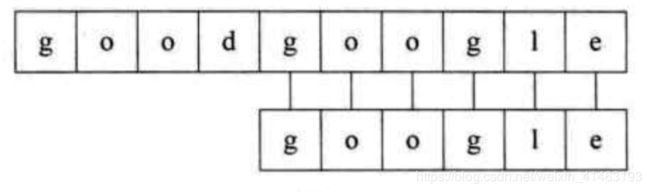
5、主串S第五位开始，S与T，6个字母全匹配，匹配成功，如下图所示

用基本的数组来实现同样的模式匹配算法Index，代码如下

（假设主串S和要匹配的子串T的长度存在S[0]与T[0]中）

/* 返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。 */
/* 其中,T非空,1≤pos≤StrLength(S)。 */
int Index(String S, String T, int pos) {
    int i = pos;/* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = 1;  /* j用于子串T中当前位置下标值 */
    while (i <= S[0] && j <= T[0]){ /* 若i小于S的长度并且j小于T的长度时，循环继续 */
        if (S[i] == T[j]){/* 两字母相等则继续 */
            ++i;
            ++j; 
        }else{/* 指针后退重新开始匹配 */
            i = i-j+2;/* i退回到上次匹配首位的下一位 */
            j = 1;/* j退回到子串T的首位 */
        }      
    }
    if (j > T[0]) 
        return i-T[0];
    else 
        return 0;
}

最坏的时间复杂度为：O((n - m) + 1) * m)

 

6、KMP模式匹配算法

由三位前辈发表的一个模式匹配算法，把它称之为克努特—莫里斯—普拉特算法，简称KMP算法

 

1、next数组的引用

定义一个next数组用来存储子串T各个位置的j值变化（j值，用于子串T中当前位置下标值）

其中，next的长度就是T串的长度

 

2、next数组值推导

例子1：T = "abcdex"（如下表所示）

j	123456
模式串T	abcdex
next[j]	011111

 

 

 

 

1) 当j = 1时，next[1] = 0;

2) 当j = 2时，j由1到j - 1就只有字符"a"，属于其他情况next[2] = 1;

3) 当j = 3时，j由1到j - 1串是"ab"，显然"a"与"b"不相等，属于其他情况next[3] = 1;

4) 以后同理，所以最终此T串的next[j] = 011111。

 

例子2：T = "abcabx"（如下表所示）

j	123456
模式串T	abcabx
next[j]	011123

 

 

 

 

1) 当j = 1时，next[1] = 0;

2) 当j = 2时，同上例说明，next[2] = 1;

3) 当j = 3时，同上，next[3] = 1;

4) 当j = 4时，同上，next[4] = 1;

5) 当j = 5时，此时j由1到j - 1的串是"abca"，前缀字符"a"与后缀字符"a"相等（前缀用蓝色字体表示，后缀用红色字体表示），因此可以推算出k值为2（由'p1...pk-1' = 'pj-k+1...pj-1'，得到p1 = p4），因此next[5] = 2；

6) 当j = 6时，j由1到j - 1的串是"abcab"，由于前缀字符"ab"与后缀字符"ab"相等，所以next[6] = 3;

我们可以根据经验得到如果前后缀一个字符相等，k值是2，两个字符k值是3，n个相等字符k值是n + 1

 

例子3：T = "aaaaaaaab"（如下表所示）

j	123456789
模式串T	aaaaaaaab
next[j]	012345678

 

 

 

 

1) 当j = 1时，next[1] = 0;

2) 当j = 2时，同上，next[2] = 1;

3) 当j = 3时，j由1到j - 1的串是"aa"，前缀字符"a"与后缀字符"a"相等，next[3] = 2;

4) 当j = 4时，j由1到j - 1的串是"aaa"，前缀字符"aa"与后缀字符"aa"相等，next[4] = 3;

5) 当j = 5时，......；

6) 当j = 9时，j由1到j - 1的串是"aaaaaaaa"，由于前缀字符"aaaaaaa"与后缀字符"aaaaaaa"相等，所以next[9] = 8;

 

3、KMP模式匹配算法实现

计算当前要匹配的串T的next数组代码如下

/* 通过计算返回子串T的next数组。 */
void get_next(String T, int *next) {
    int i,j;
    i=1;
    j=0;
    next[1]=0;
    while (i

 

返回子串T在主串S中第pos个字符之后的位置代码如下

/* 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数返回值为0。 */
/*  T非空，1≤pos≤StrLength(S)。 */
int Index_KMP(String S, String T, int pos) {
    int i = pos;		/* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = 1;			/* j用于子串T中当前位置下标值 */
    int next[255];		/* 定义一next数组 */
    get_next(T, next);	/* 对串T作分析，得到next数组 */
    while (i <= S[0] && j <= T[0]){/* 若i小于S的长度并且j小于T的长度时，循环继续 */
        if (j==0 || S[i] == T[j]){/* 两字母相等则继续，与朴素算法增加了j=0判断 */
            ++i;
            ++j; 
        }else{/* 指针后退重新开始匹配 */
            j = next[j];/* j退回合适的位置，i值不变 */
        }
    }
    if (j > T[0]) 
        return i-T[0];
    else 
        return 0;
}

整个算法的时间复杂度为O(n + m)。

 

4、KMP模式匹配算法改进

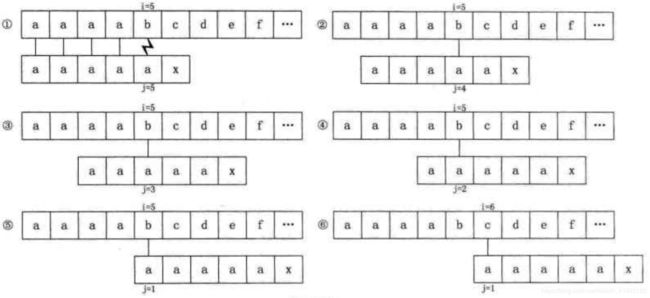
如果我们的主串S = "aaaabcde"，子串T = "aaaaax"，其next数组值分别为012345。

在一开始当i = 5, j = 5时，"b" 与 "a"不相等，如下图的①，因此j = next[5] = 4，如下图的②

此时"b"与第4位置的"a"依然不相等，j = next[4] = 3，如图中的③，后依次是④⑤，直到j = next[1] = 0

根据算法，此时i++、j++，得到的i = 6，j = 1，如图中的⑥

其中的②③④⑤，其实是多余的判断。

由于T串的第二、三、四、五位置的字符都与首位的"a"相等，那么可以用首位next[1]的值去取代与它相等的字符后续next[j]的值。

 

使用nextval取代next数组，代码如下

/* 求模式串T的next函数修正值并存入数组nextval */
void get_nextval(String T, int *nextval) {
    int i,j;
    i=1;
    j=0;
    nextval[1]=0;
    while (i

 实现匹配算法，只需要将"get_next(T, next);"改为"get_nextval(T, next);"即可。

 

5、nextval数组值推导

改良后，我们之前的例子nextval值就与next值不完全相同了，比如

例子1：T = "ababaaaba"（如下表所示）

j	123456789
模式串T	ababaaaba
next[j]	011234223
nextval[j]	010104210

 

 

 

 

 

先算出next数组的值分别为011234223，再分别判断：

1) 当j = 1时，nextval[1] = 0;

2) 当j = 2时，因第二位字符"b"的next值是1，而第一位就是"a"，它们不相等，所以nextval[2] = next[2] = 1，维持原值。

3) 当j = 3时，因第三位字符"a"的next值是1，所以与第一位的"a"相等，所以nextval[3] = next[1] = 0。

4) 当j = 4时，因第四位字符"b"的next值是2，所以与第二位的"b"相等，所以nextval[4] = next[2] = 1。

5) 当j = 5时，next值是3，第五位字符"a"与第三位的"a"相等，所以nextval[5] = next[3] = 0。

6) 当j = 6时，next值是4，第六位字符"a"与第四位的"b"不相等，所以nextval[6] = 4。

7) 当j = 7时，next值是2，第七位字符"a"与第三位的"b"不相等，所以nextval[7] = 2。

8) 当j = 8时，next值是2，第八位字符"b"与第二位的"b"相等，所以nextval[8] = next[2] = 1。

9) 当j = 9时，next值是3，第九位字符"b"与第三位的"a"相等，所以nextval[9] = next[3] = 0。

 

例子2：T = "aaaaaaaab"（如下表所示）

j	123456789
模式串T	aaaaaaaab
next[j]	012345678
nextval[j]	000000008

 

 

 

 

 

先算出next数组的值分别为012345678，再分别判断：

1) 当j = 1时，nextval[1] = 0；

2) 当j = 2时，next值是1，第二位字符与第一位字符相等，所以nextval[2] = next[2] = 0；

3) 同样的道理，其后都为0......；

4) 当j = 9时，next值是8，第九位字符"b"与第八位的"a"不相等，所以nextval[9] = 8。

总结改进过的KMP算法，它是在计算出next数组的同时，如果a位字符与它next值指向的b位字符相等，则该a位的nextval就指向b位的nextval值，如果不等，则该a位的nextval值就是它自己a位的next的值。

 

总结

在使用这些函数的同时，也要理解它们当中的原理，以便在碰到复杂的问题时，可以更加灵活的使用

比如KMP模式匹配算法的学习，就是更有效地去理解index函数当中的实现细节，加油！！！