GAN入门实现MNIST数据集生成

参考：https://www.cnblogs.com/bonelee/p/9166084.html

GAN框架

对抗式生成网络GAN(Generative Adversarial Net)，是一个非常流行的生成式模型。 GAN 有两个网络，一个是 生成器generator，用来生成伪样本；一个是判别器 discriminator，用于判断样本的真假。通过两个网络互相博弈和对抗来达到最好的生成效果，示意图如下：

首先介绍KL散度(KL divergence)，用于衡量两种概率分布的相似程度，数值越小，表示两种概率分布越接近。离散的概率分布：
$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}$$
连续的概率分布：
$$D_{KL}(P||Q)={\int }_{-\infty }^{\infty }P(x)\log \frac{P(x)}{Q(x)}dx$$
设真实样本集服从分布$P_{data}(x)$,其中$x$是一个真实样本。生成器产生的分布设为$P_G(x;\theta )$,$\theta$是生成器G的参数，通过优化$\theta$使得$P_G(x;\theta )$和$P_{data}(x)$尽可能接近，也就是生成的图片与真实分布一致。
从真实数据分布$P_{data}(x)$里面取样$m$个点，$\{x^1,x^2,...,x^m\}$,根据给定的参数$\theta$可以计算出生成这$m$个样本数据的似然为：$$L=\prod _{i=1}^m{P}_G(x^i;\theta )$$
${\theta }^{\ast }$为最大化似然的结果：
$$\begin{gathered} {\theta }^{\ast }=\arg \underset{\theta }{\max }\prod _{i=1}^m{P}_G(x^i;\theta ) \\ \propto \arg \underset{\theta }{\max }\sum _{i=1}^m\log P_G(x^i;\theta ) \\ \approx \arg \underset{\theta }{\max }{E}_{x\sim P_{data}}[\log P_G(x;\theta )] \\ =\arg \underset{\theta }{\max }{\int }_x{P}_{data}(x)\log P_G(x;\theta )dx \\ \propto \arg \underset{\theta }{\max }\{{\int }_x{P}_{data}(x)\log P_G(x;\theta )dx-{\int }_x{P}_{data}(x)\log P_{data}(x)dx\} \\ =\arg \underset{\theta }{\max }{\int }_x{P}_{data}(x)\log \frac{P_G(x;\theta )}{P_{data}(x)}dx \\ =\arg \underset{\theta }{\max }KL(P_{data}(x)||P_G(x;\theta )) \end{gathered}$$
$z$是随机噪声，服从正态分布或均匀分布$P_{prior}(z)$，通过生成器$G(z)=x$生成图片，$$P_G(x;\theta )={\int }_z{P}_{prior}(z)I_{[G(z)=x]}dz$$
其中$I_{[G(z)=x]}$为示性函数：
$$I_{G(z)=x}=\{\begin{array}{c}0,G(z)̸=x\\ 1,G(z)=x\end{array}$$
这样无法通过最大似然对生成器参数$\theta$进行求解。因此采用判别器D分类$P_G(x)$与$P_{data}(x)$产生的误差$V(G,D)$来取代极大似然估计。

下面是训练判别器的示意图，此时的生成器的权重被固定，真实图片和生成图片都会输入到判别器中：

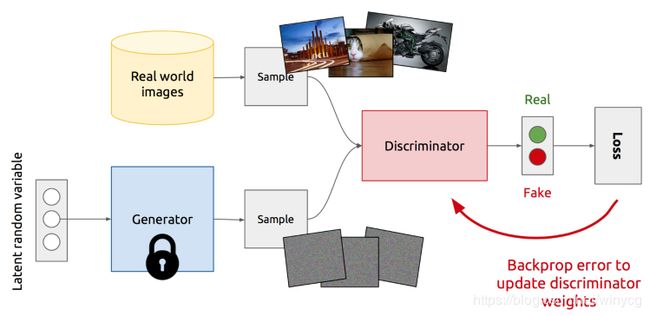
下面是训练生成器的示意图，此时的判别器的权重被固定，生成图片输入到判别器中：

误差

对于判别器来说，希望能够正确地分类真样本和假样本，所以需要最小化分类误差，也可以说是最大化奖励$V(D,G)$，这里奖励就是交叉熵的负数形式：
$$V(D,G)={\mathbb{E}}_{x\sim P_{data}}[\log D(x)]+{\mathbb{E}}_{x\sim P_{gen}}[\log (1-D(x))]$$
对于上述的奖励函数，需要优化判别器D和生成器G两个参数，此时可以采用的方法是固定一个优化另外一个。对于D来说，希望最大加奖励V(D,G)，对于生成器来说，希望最小化奖励V(D,G),也就是说希望生成的图片能骗过生成器。此时的优化目标为：$$\underset{G}{\min }\underset{D}{\max }V(D,G)$$
当博弈达到纳什平衡（Nash equilibrium）时，i.e.,$P_{data}(x)=P_{gen}(x)\forall x$,$D(x)=0.5$,G是最优的。

训练过程

在一个epoch中，首先使用真实图片和generator生成的假图片来训练discriminator是否能判别真假，即是二分类问题。之后只用generator生成假图片在discriminator的误差来训练generator。

GAN优缺点

优点：

• 抽样和生成很简单直接。
• 训练不涉及最大似然估计。
• 生成器不接触真实样本，对过拟合具有健壮性。
• 实验上，GAN擅长捕获分布的模式。

缺点：

• 生成样本的概率分布是隐式的，无法直接计算概率。因此vanilla GANs只能用于生成样本。
• 训练不收敛。SGD通常在确定的条件下找到最有参数，可能不会收敛到一个Nash平衡点。
• mode-collapse模式坍塌。一般出现在GAN训练不稳定的时候，具体表现为生成出来的结果非常差，但是即使加长训练时间后也无法得到很好的改善。
  
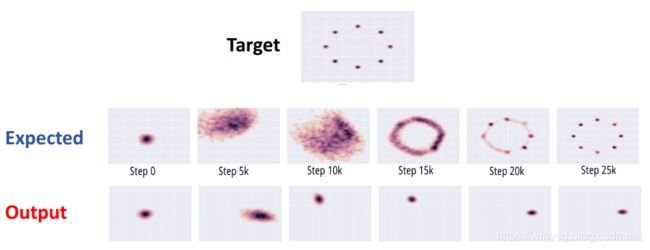
  具体原因可以解释如下：GAN采用的是对抗训练的方式，G的梯度更新来自D，所以G生成的好不好，需要凭借D的判断。但是如果某一次G生成的样本可能并不是很真实，但是D给出了正确的评价，或者是G生成的结果中一些特征得到了D的认可，这时候G生成的结果是正确的，那么接下来通过D生成的样本还会得到高的评价，实际上G生成的并不怎么样，但是他们两个就这样自我欺骗下去了，导致最终生成结果缺失一些信息，特征不全。

GAN生成MNIST数据集

以下使用GAN来生成手写数字。

import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
from torchvision.utils import save_image

z_dimension = 100  # the dimension of noise tensor


class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()
        self.dis = nn.Sequential(
            nn.Linear(784, 256),
            nn.LeakyReLU(0.2),
            nn.Linear(256, 256),
            nn.LeakyReLU(0.2),
            nn.Linear(256, 1),
            nn.Sigmoid()
        )

    def forward(self, x):
        x = self.dis(x)
        return x


class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
        self.gen = nn.Sequential(
            nn.Linear(z_dimension, 256),
            nn.ReLU(True),
            nn.Linear(256, 256),
            nn.ReLU(True),
            nn.Linear(256, 784),
            nn.Tanh()
        )

    def forward(self, x):
        x = self.gen(x)
        return x


transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize([0.5], [0.5]),
])

trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True)

testset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False)

def to_img(x):
    out = 0.5 * (x + 1)  # 将x的范围由(-1,1)伸缩到(0,1)
    out = out.view(-1, 1, 28, 28)
    return out

D = Discriminator().to('cpu')
G = Generator().to('cpu')

criterion = nn.BCELoss()
D_optimizer = torch.optim.Adam(D.parameters(), lr=0.0003)
G_optimizer = torch.optim.Adam(G.parameters(), lr=0.0003)

# Training
def train(epoch):
    print('\nEpoch: %d' % epoch)
    D.train()
    G.train()
    all_D_loss = 0.
    all_G_loss = 0.
    for batch_idx, (inputs, targets) in enumerate(trainloader):
        inputs, targets = inputs.to('cpu'), targets.to('cpu')
        num_img = targets.size(0)
        real_labels = torch.ones_like(targets, dtype=torch.float)
        fake_labels = torch.zeros_like(targets, dtype=torch.float)
        inputs_flatten = torch.flatten(inputs, start_dim=1)

        # Train Discriminator
        real_outputs = D(inputs_flatten)
        D_real_loss = criterion(real_outputs, real_labels)

        z = torch.randn((num_img, z_dimension))  # Random noise from N(0,1)
        fake_img = G(z)  # Generate fake images
        fake_outputs = D(fake_img.detach())
        D_fake_loss = criterion(fake_outputs, fake_labels)

        D_loss = D_real_loss + D_fake_loss
        D_optimizer.zero_grad()
        D_loss.backward()
        D_optimizer.step()

        # Train Generator
        z = torch.randn((num_img, z_dimension))
        fake_img = G(z)
        G_outputs = D(fake_img)
        G_loss = criterion(G_outputs, real_labels)
        G_optimizer.zero_grad()
        G_loss.backward()
        G_optimizer.step()

        all_D_loss += D_loss.item()
        all_G_loss += G_loss.item()
        print('Epoch {}, d_loss: {:.6f}, g_loss: {:.6f} '
              'D real: {:.6f}, D fake: {:.6f}'.format
              (epoch, all_D_loss/(batch_idx+1), all_G_loss/(batch_idx+1),
               torch.mean(real_outputs), torch.mean(fake_outputs)))

    # Save generated images for every epoch
    fake_images = to_img(fake_img)
    save_image(fake_images, 'MNIST_FAKE/fake_images-{}.png'.format(epoch + 1))


for epoch in range(40):
    train(epoch)
    
torch.save(G.state_dict(), './generator.pth')
torch.save(D.state_dict(), './discriminator.pth')

运行40轮得到的结果：

在训练完之后，可以得到generator的参数，可以将其单独剥离出来进行图像生成。此时，给generator任意生成的符合先验分布的噪声向量，就会生成对应的图片：

import torch
import torch.nn as nn
from torchvision.utils import save_image

z_dimension = 100  # the dimension of noise tensor


class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
        self.gen = nn.Sequential(
            nn.Linear(z_dimension, 256),
            nn.ReLU(True),
            nn.Linear(256, 256),
            nn.ReLU(True),
            nn.Linear(256, 784),
            nn.Tanh()
        )

    def forward(self, x):
        x = self.gen(x)
        return x

def to_img(x):
    out = 0.5 * (x + 1)
    out = out.view(-1, 1, 28, 28)
    return out


G = Generator().to('cpu')
G.load_state_dict(torch.load('./generator.pth'))


def generate_synthetic_images(num_img):
    G.eval()
    z = torch.randn((num_img, z_dimension))
    fake_img = G(z)

    fake_images = to_img(fake_img)
    print(fake_img)
    save_image(fake_images, 'MNIST_GEN/synthetic_images.png')


if __name__ == '__main__':
    generate_synthetic_images(100)