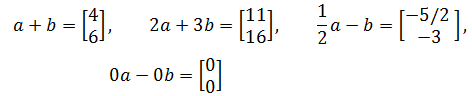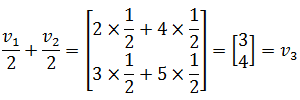线性代数基础一

转自：https://www.cnblogs.com/bigmonkey/p/9566796.html

向量空间又称线性空间，是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后，使许多问题的处理变得更为简洁和清晰，在此基础上的进一步抽象化，形成了与域相联系的向量空间概念。

线性组合

　　线性组合（liner combinations）这个概念曾经被多次提到，如果v1,v2…vn是n维向量，即vi∈Rn，那么t1v1 + t2v2 + … + tnvn就是v1,v2…vn 的线性组合，ti∈R。从定义可以看出，线性组合仅包括乘法和加法，只有同阶向量才涉及到线性组合。

　　如果有两个二维向量：

 

　　下面是可能存在的线性组合：

 

　　最后一个组合最终得到零向量，零向量也是一个线性组合。此外，按照惯例，单个向量用列向量表示。

　　单个向量同样存在线性组合。下面是a可能存在的线性组合：

向量空间

　　概念没什么好解释的，经常提到二维空间R2，三维空间R3，n维空间Rn，这些就是向量空间。

　　以R2空间为例，如果有两个指向不同方向的非零向量a和b，那么R2空间的所有向量都可以用a和b的线性组合得出；a和b的所有线性组合都在R2空间内。这也意味着，向量空间对向量的所有线性组合封闭。下面是一个不封闭的例子，如果定义R2的第一象限是向量a(1,1)的向量空间，那么a的所有线性组合应该全部在第一象限内，但是 –a却落在了其它象限，所以第一象限不对a封闭，也不是a的向量空间。

向量张成的空间

　　如果几个向量的线性组合在某一个向量空间中，并且该向量空间仅包括这几个向量的线性组合，那么这个向量空间就叫做这几个向量张成的空间。简单地说，N个向量张成的空间就是N个向量的线性组合。

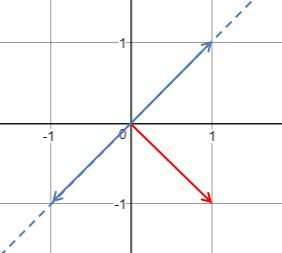
　　以R2空间为例，如果有两个指向不同方向的非零向量a和b，那么a,b张成的空间就是R2，用span(a, b) = R2 表示。如果是两个平行的向量，a’ = <1, 1>，b’ = <-1, -1>，那么它们无法张成R2，因为无论怎样线性组合，也不可能得到<1, -1>，实际上，a’b’ 张成的空间是一条直线：

　　同样，span(a)张成的空间也仅仅是a的伸缩，所以span(a)也是一条直线。很明显，0向量张成的向量空间还是0向量。

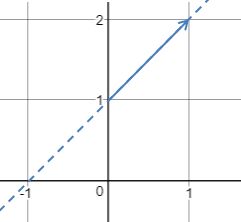
　　需要注意的是，a是经过原点的，如果很不幸地将a画在了别的地方，它张成的空间就不是直线了，因为其中一个线性组合0a并不在直线上：

线性相关和线性无关

　　如果有两个向量<2,3>和<4, 6>，它们张成的空间是什么呢？

 

　　根据定义，这两个向量的线性组合是：

 

　　这相当于单个向量<2, 3>的线性组合，是一条直线。实际上，这正是过原点的直线参数方程（直线的参数方程可参考《线性代数笔记6——直线和曲线的参数方程》）。

　　上面的两个向量就是线性相关的，这意味着它们中的一个可以用另一个的线性组合表示，也就是说其中一个向量是多余的，或者说它们不是独立向量（对同一种现象，线性代数从不同的角度会有多种叫法，这多少令人迷惑）。与之相反，就是线性无关。

　　再来一组向量，看看它们是线性相关还是线性无关？

　　看起来是线性无关的，其中一个向量无论再怎么增大，都无法表示另一个，但是线性组合不仅仅包括数乘：

　　v3是v1v2的线性组合，所以这三个向量是线性相关的。换个角度看，v1v2是线性无关的，span(v1, v2) = R2，R2中的每个向量都可以由v1, v2的线性组合表示，而v3∈R2，所以v3也可以由v1, v2的线性组合表示，它是个多余向量（当然，也可以说v1或v2是多余的，因为三者中的任意一个都可以由另外两个表示，所以三者等价），对张成空间没有任何贡献，因此v1v2 v3是线性相关的。span(v1, v2, , v2) = R2

　　有了上面的铺垫，可以用数学语言描述线性相关的定理：如果存在一个集合S = {v1, v2,…,vn}，当这个集合满足t1v1 + t2v + … + tnvn = Z 时，S中的向量是线性相关的，其中Z是0向量，ti∈R，ti 不全为0。

　　这似乎有些让人困惑，如果换一种写法就很清晰了。假设t1 ≠ 0：

　　现在可以看出，定理描述的是，v1可以用其它向量的线性组合表示。在判断线性相关的时候，定理提供了一种有效的方案。

　　现在有两个向量：

 

　　或许很容易看出它们是线性无关的，现在根据上面数学描述看一种新方案：

 

　　现在判断线性相关变成了解方程组的问题，因为这个方程组解得t1 = 0, t2 = 0，所以两个向量是线性无关的，t1t2至少有一个不为0才是线性相关。

子空间

　　设V是 Rn的一个非空子集，若V中的任意N个向量的线性组合依然属于V，则称V是 Rn的一个线性子空间，简称子空间。

　　根据概念，如果V是Rn的线性子空间，则V一定满足三个条件，

1. 包含0向量；
2. x是V中的一个向量，x和一个标量的乘积也在V中，即数乘封闭性；
3. a和b是V中的向量，a+b也在V中，即加法封闭性。

　　上面的2、3可以看作是V中任意两个向量的线性组合。

　　对于R2来说，它的子空间有三个， R2本身、Z、所有经过原点的直线。

　　对于R3来说，它的子空间有四个， R3本身、Z、所有经过原点的直线、所有经过原点的平面。

　　来看一个例子，下面的V是否是R2的子空间？

 

　　可以通过分量的取值范围得知，V是直角坐标系的一、四象限：

　　可以根据子空间的条件逐一检验，首先0向量在V内；再看加法封闭性，这样定义V中的任意两个向量：

 

　　由于a1+a2 ≥ 0，所以满足加法封闭性。最后看乘法封闭性，当标量为负数时，其结果已经超出了一、四象限，不在V中，所以不满足乘法封闭性，V不是R2的子空间。

　　最后，向量集合张成的空间一定是子空间，所以也经常说“向量张成的子空间”。

子空间的基

　　简单地说，基就是张成子空间所需要的最小向量集。

　　如果一个向量集S={v1, v2 … vn}中的向量是线性无关的，S张成了一个子空间V，S就叫做V的一组基，{v1, 2v2, 3v3 … nvn} 是另一组基，但是它和第一组没什么本质区别。

　　下面的集合S1和S2都是R2的一组基：

 

　　因为S2中的两个向量是R2空间两个维度上的单位向量，所以S2也叫做R2的标准基。