标准DH建模与改进DH建模(三)—— 怎么用改进DH法
能力强的大佬可以直接看原文《A new geometric notation for open and close-loop robots》
另外,只想学习怎么使用改进DH法可以直接看第四节
0.前言
本论文讲解一种新的,用来给串联,并联,树状机器人建模的方法(我们只介绍开环结构,如果你对其他结构感兴趣请看原文)。
DH建模法对于串联机械臂来说十分实用,但是对于并联结构甚至是树形结构的机器人并不适用,文章介绍的新的建模方法正是从DH方法推导而来,该方法在改进了DH法的一些不足的同时,仍然保留了其优点。
1.介绍
对于串联机械臂有很多种建模方法,其中最著名的就是DH建模法了,DH法用4个参数描述每个关节坐标系。DH在串联机械臂建模上面十分强大,但是难以用于并联结构的机器人。
Sheth and Uicker(简称S-U)发明了另一种用7个参数描述每个连杆的建模方法,这里我们简称为S-U法,该方法的优点就是可以用于任何机械结构,但是由于它过于复杂,因此一般我们在面对并联结构时才会用这个方法。
本文介绍的新的建模方法结合了DH方法的简单以及SU方法的强大。第二节和第三节我们分别回顾DH法和SU法,第四节介绍我们新的建模方法,第五节用是用新的建模思路建模的两个例子
2.DH建模法回顾
(这里不再赘述)
3.S-U建模法
(科普了,不看无妨)
鉴于DH法无法用于并联结构,Seth 和 Uicker 发明了S-U建模法,该方法包含两个部分:
- 一个常数部分来指明连杆的形状
- 一个变量部分来代表关节的运动
下图展示了两个相连的连杆,每个连杆包含了两个坐标系。

S-U 法把关节的表达分成了两个坐标系分别在前后两个连杆上面:(这也不难理解,每个转动关节是不是由两个连杆组成?或者说一个导轨是不是包含滑块和滑轨?)
- 对于前一个连杆Li上的坐标系XjYjZj(我们称其为Rj-),Zj指明了转动关节的方向,XjYj可以任意选
- 对于后一个连杆Lj上的坐标系UjVjWj(我们称其为Rj+),Wj指明了转动关节的方向,UjVj可以任意选
- 关节j的转动量用qj表示
现在,我们定义连杆的形状以及关节的运动
3.1 Shape matrix 形状矩阵
Lj的形状是由Rj+和Rk-的相对变换来描述的,因此我们只要知道Rj+和Rk-之间的相对变换,就能表达出Lj的形状。为了达成这个目的,我们还需要找到Wj和Zk的公共垂线tjk,然后下面用6个参数来描述两个坐标系的相对变换:
- ajk:Wj与Zk在tjk方向上的距离
- αjk:从正的Wj轴到正的Zk轴关于tjk方向上的转角
- bjk:tjk与Xk在Zk方向上的距离
- βjk:从tjk轴到正的Xk轴关于Zk方向上的转角
- rjk:Uj与tjk在Wj方向上的距离
- γjk:从正的Uj轴到正的tjk轴关于Wj方向上的转角
我们用Fjk来表示link(j)的形状,这同时也是关节j到关节k的转换:
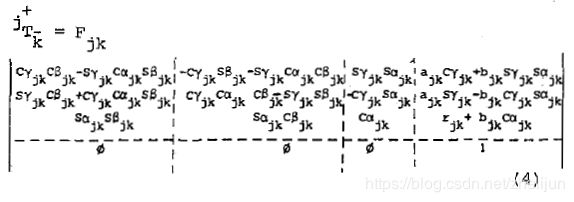
3.2 Joint Matrix 关节矩阵
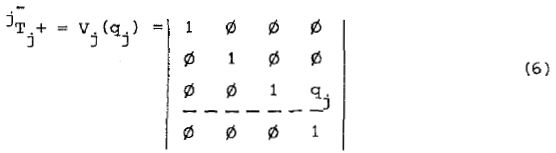
描述完了连杆的形状,我们现在描述关节的运动。我们用关节矩阵Vj(qj)来描述关节运动,其中qj代表第j个关节的关节变量。之前我们提到过一个关节由两个坐标系Rj+和Rj-组成,关节矩阵Vj(qj)正描述了Rj-到Rj+的变换。这里我们需要分成转动关机和平动关节来考虑(只是坐标系简单的旋转和平移变换,相信大家很熟悉了,我直接贴结论):
3.3 转换矩阵
有了形状矩阵和关节运动矩阵之后,转换矩阵就很容易了。于是对于figure 3的这个结构,Rj-到Rk-的转换矩阵为:
![]()
要得到完整的机器人动力学方程只需要从第一个坐标系乘到最后一个坐标系即可。
4. 本文要介绍的改进建模法
4.1 介绍
该方法可用于开环,闭环以及树形结构机器人。我们这里只介绍串联结构。有兴趣了解并联以及树形结构的可以自行看原文。
4.2 串联机器人
4.2.1 建系规则
首先我们需要建立坐标系,建系所要遵循的四个规则:
- 一个串联机器人包括n+1个连杆,link(0)是固定的基坐标系,link(n)是最后一根连杆。joint(i)连接了link(i-1)和link(i)
- 用Ri表示对应于link(i)的坐标系
- Zi表示joint(i)的方向
- Xi 定义为Zi 以及Zi+1的公共垂线(Xi必须要同时与Zi以及Zi+1相交)
4.2.2 准备建系
我个人的建系顺序如下:
- 定义好连杆,关节并找到关节轴
- 根据上面说的最后一个条件找到X轴
- 根据右手定则找到Y轴
- 加上tool frame,如果tool frame不满足上述条件4的话解决办法跟标准DH无异,参见这里
4.2.3 写出参数表
由下图,我们需要以下四个参数来表达从坐标系i到坐标系i-1的转换
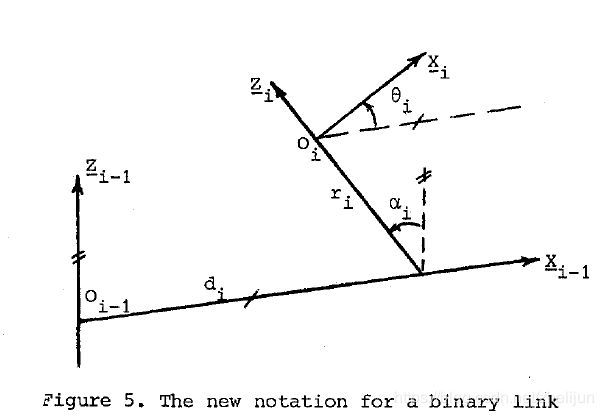
- αi:Zi-1轴与Zi轴关于Xi-1的夹角
- di:oi-1与Zi关于Xi-1的距离
- ri:oi与Xi-1关于Zi的距离
- θi:Xi-1轴与Xi轴关于Zi的夹角
类似于DH法里面,我们需要分两种情况讨论。如果是转动关节,那么qi = θi;如果是平动关节,那么qi = ri。
4.2.4 最后写出坐标系转换矩阵
有了上面这些表达方式之后,我们根据坐标变换得到坐标系i-1到坐标系i的转换关系为:

建系时作者提供了两个简化方法(我还没验证):
- 当q1=0的时候,R0可以跟R1定义在一起,此时α1 = d1 = 0
- 当qn = 0 时,Xn可以与Xn-1重合
有了上述坐标系转换方程之后我们就可以通过
![]()
得到整个串联机器人的动力学方程(如需要知道基坐标到tool tip的转换矩阵,还需要再乘一个nTtool)。
5. 建模举例(结果还未验证,本节仅供参考)
这是论文提供的例子,没给机械结构照片,而且似乎做了简化,有点抽象。下一篇我们用一个更简单的例子来说明。
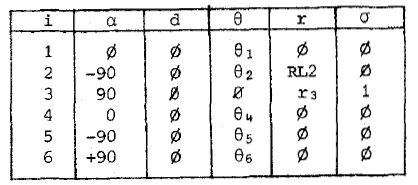
经典的斯坦福机械臂
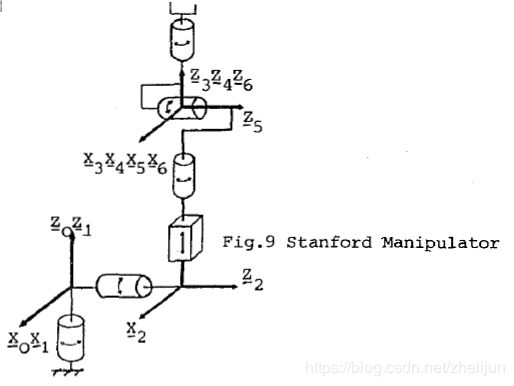
用本文所讲的方法建模得到
6.小结
本文介绍了一种新的建模方法,初衷是让大家知道怎么运用该建模方法使用软件Open symoro。我们并没有深入讲解该建模方法的优越性具体体现在哪,以及怎么用该方法给并联结构和树状结构机器人建模(因为我暂时只用到这些知识)。有兴趣的可以看英文原文