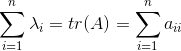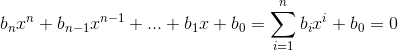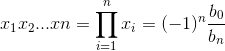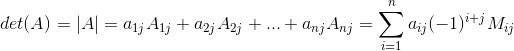线性代数——韦达定理、矩阵行列式、矩阵的迹、矩阵特征值及关系
本文主要围绕以下定理,并对相关知识点做回顾和扩充。
定理:设![]() ,...,
,...,![]() (实数或者复数,可以重复)是
(实数或者复数,可以重复)是![]() 阶方阵
阶方阵![]() 的
的![]() 个特征值,即
个特征值,即![]() ,则
,则
通俗描述即为:矩阵的特征值之和等于矩阵的迹,矩阵的特征值之积等于矩阵的行列式。
以下分为五个部分介绍:
- 韦达定理
- 矩阵行列式
- 矩阵的迹
- 矩阵的特征值及特征向量
- 解释矩阵的特征值之和等于矩阵的迹,之积等于矩阵的行列式
一、韦达定理
韦达定理说明了一元二次方程中根和系数之间的关系。
1、一元二次方程
对于一元二次方程![]() (
(![]() 且
且![]() ),设两个根为
),设两个根为![]() ,
,![]() 。
。
以上定理交代了两根之和(积)与方程系数的关系。
2、一元三次方程
对于一元三次方程![]() ,设三个根为
,设三个根为![]() ,
,![]() ,
,![]() 。
。
3、一元多次方程
推广定理:韦达定理不仅可以说明一元二次方程根与系数的关系,还可以推广说明一元n次方程根与系数的关系。
即:所有根之和为(n-1)次项系数与n次项系数之比的相反数,所有根之积为常数项与n次项系数之比再乘以![]()
注:该推广形式的证明一般无法根据求根公式进行,因为5次以上的一元方程没有求根公式。证明步骤较繁琐,是通过将左边的多项式因式分解成![]() 之后,再去括号,比较相同次数的项的系数从而得出结论。这个方法具有普遍性,即使是有求根公式的方程,亦可以通过该方法证明韦达定理,而无需借助求根公式。
之后,再去括号,比较相同次数的项的系数从而得出结论。这个方法具有普遍性,即使是有求根公式的方程,亦可以通过该方法证明韦达定理,而无需借助求根公式。
二、矩阵行列式
1、矩阵行列式的基本介绍
一个![]() 的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:
的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:
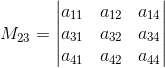
把一个![]() 阶行列式中的元素
阶行列式中的元素![]() 所在的第
所在的第![]() 行和第
行和第![]() 列划去后,留下来的
列划去后,留下来的![]() 阶行列式叫做元素
阶行列式叫做元素![]() 的余子式,记作
的余子式,记作![]() 。记
。记![]() ,叫做元素
,叫做元素![]() 的代数余子式。例如:
的代数余子式。例如:
注意:余子式和代数余子式是行列式中才有的概念。如上所示,此时的![]() 代表行列式,
代表行列式,![]() 代表元素
代表元素![]() 的余子式,
的余子式,![]() 代表元素
代表元素![]() 的D代数余子式。
的D代数余子式。
命题:n阶行列式det(A)等于它的任一行(列)的所有元素与其对应的代数余子式的乘积之和:
2、矩阵行列式的几何理解
一句话概括之,行列式的本质就是线性变换的放大率(伸缩因子)。
几何理解:![]() 表示
表示![]() 维空间到
维空间到![]() 维空间的线性变换,假想原来空间中有一个
维空间的线性变换,假想原来空间中有一个![]() 维的“立方体”(任意形状),其中“立方体”内的每一个点都经过这个线性变换,变成
维的“立方体”(任意形状),其中“立方体”内的每一个点都经过这个线性变换,变成![]() 维空间中的一个新立方体,设原立方体的体积为
维空间中的一个新立方体,设原立方体的体积为![]() ,新立方体的体积为
,新立方体的体积为![]() ,行列式
,行列式![]() 。
。
1)线性变换
理解行列式之前,需要先理解线性变换。
线性代数中的线性变换:转换矩阵![]() 乘以向量
乘以向量![]() 就是对其进行了线性变换,从而得到转换之后的向量
就是对其进行了线性变换,从而得到转换之后的向量![]() 。
。
线性变化中的“”线性”二字,也就是原来的一条直线,在变换了之后还应该是直线。
任何一个空间都可以由一组基构成,也就是说,这个空间上的任何一个点(向量)都可以由这组基以线性组合的形式得到。
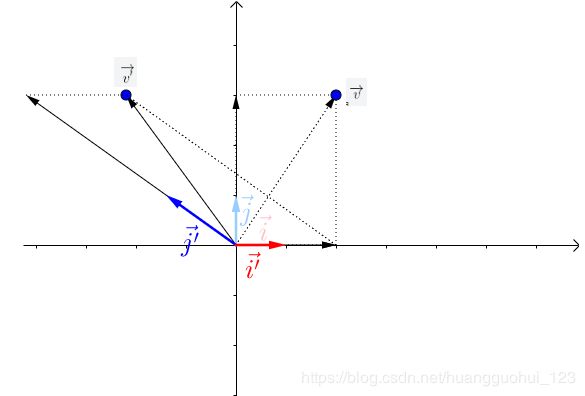
假设我们有原向量![]() ,变换(旋转)矩阵
,变换(旋转)矩阵![]() ,从而得到转换之后的向量
,从而得到转换之后的向量。
从基向量的角度解释:矩阵![]() 对向量
对向量![]() 的变换,其实是施加在其基底上的变换,而新的向量
的变换,其实是施加在其基底上的变换,而新的向量![]() 关于新的基底
关于新的基底![]() 的线性组合,与原来的向量
的线性组合,与原来的向量![]() 是关于基底
是关于基底![]() 的线性组合是一样的。
的线性组合是一样的。![]() ,
,![]() ,
,![]() ,线性组合系数为(2,3),
,线性组合系数为(2,3),![]() ,
,![]() 经过矩阵
经过矩阵![]() 的线性变换之后变成新的基底
的线性变换之后变成新的基底![]() ,
,![]() ,新向量
,新向量![]() 。
。
注意:关于旋转矩阵的由来及推导可见《线性代数——线性变换——旋转矩阵(泰勒公式、虚数、欧拉公式)》
所以我们说,一个向量,在经过一个矩阵![]() 的变换之后,改变的是组成向量的基,而这个向量关于基的线性组合方式是没有变化的。
的变换之后,改变的是组成向量的基,而这个向量关于基的线性组合方式是没有变化的。
换句话说,对于一个线性变换,我们只需要跟踪其基在变换前后的变化,便可以掌握整个空间的变化。而矩阵![]() 的列其实与变换后新的基底之间有着某些联系,也就是说,新的基底其实就是矩阵
的列其实与变换后新的基底之间有着某些联系,也就是说,新的基底其实就是矩阵![]() 的列向量的线性组合
的列向量的线性组合![]() ,其中
,其中![]() 是
是![]() 的列。
的列。
以上的图形展现的是“旋转”的线性变化,其本质是改变组成向量的基。接下来我们“推移”是怎么改变基的,如下图。
推移矩阵把![]() 推移到
推移到![]() 实际上也是改变了
实际上也是改变了![]() 的基底
的基底![]() 。
。
从基向量的角度解释:设![]() ,
,![]() ,
,![]() ,线性组合系数为(2,3);
,线性组合系数为(2,3);![]() ,
,![]() 经过矩阵
经过矩阵![]() 的线性变换之后变成新的基底
的线性变换之后变成新的基底![]() ,
,![]() ,新向量
,新向量![]() 。
。
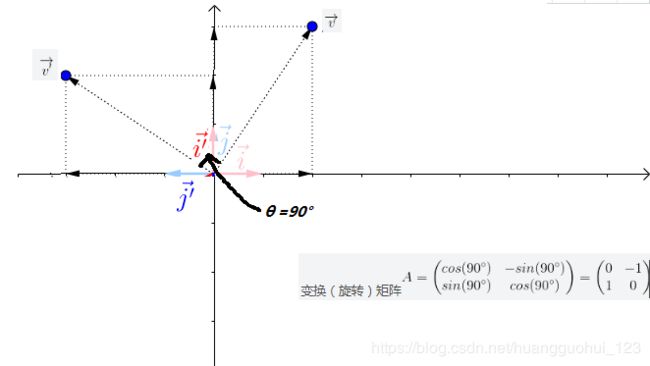
2)行列式的几何理解
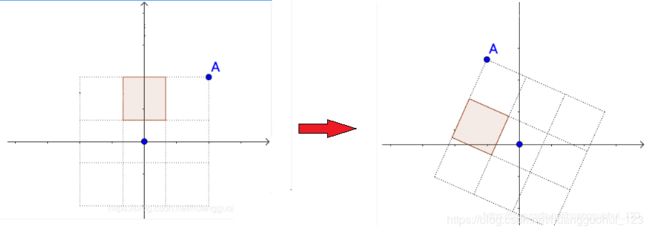
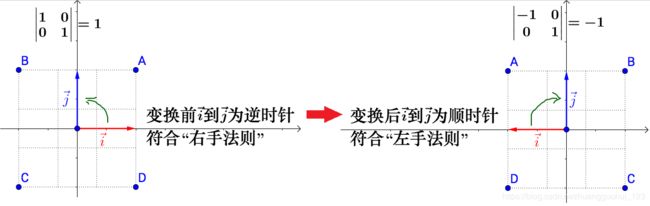
以上面的旋转矩阵![]() 为例,我们对其求行列式
为例,我们对其求行列式![]() ,意味旋转矩阵的行列式恒等于1,且不改变面积(或体积),如下图二维平面的旋转展示。
,意味旋转矩阵的行列式恒等于1,且不改变面积(或体积),如下图二维平面的旋转展示。
即和上面的结论相符:行列式是线性变换的伸缩因子。
且我们容易得到:
3)行列式的性质
由上面我们已经知道,行列式是线性变换的伸缩因子,所以很容易得到:
![]()
从“体积”的角度理解为:两次对“体积”的缩放效果是累积的,且和两次操作次序无关。
4)“矩阵![]() 可逆” 完全等价于 “
可逆” 完全等价于 “![]() ”
”
公式推导
由上面我们已知:![]()
且有逆矩阵的性质:![]() (
(![]() 为单位矩阵)
为单位矩阵)
结合可得:![]()
几何理解
![]() 可以理解为线性变换矩阵
可以理解为线性变换矩阵![]() 把
把![]() 维立方体给拍扁了(原来
维立方体给拍扁了(原来![]() 维变成了
维变成了![]() 维或
维或![]() 维,....),例如把3维立方体拍成2维的纸片,纸片体积多少呢?当然是 0 啦!
维,....),例如把3维立方体拍成2维的纸片,纸片体积多少呢?当然是 0 啦!
注意:这里说的体积都是针对![]() 维空间而言的,
维空间而言的,![]() 就表示新的立方体在
就表示新的立方体在![]() 维空间体积为0,但是可能在
维空间体积为0,但是可能在![]() 维还是有体积的,只是在
维还是有体积的,只是在![]() 维空间的标准下为0而已。好比一张纸片,“2维体积”也就是面积可以不为0,但是“3维体积”是0。
维空间的标准下为0而已。好比一张纸片,“2维体积”也就是面积可以不为0,但是“3维体积”是0。
所以凡是![]() 的矩阵
的矩阵![]() 都是不可逆的,因为这样的变换以后就再也找不到一个矩阵将其变换回去,这样的矩阵必然是没有逆矩阵
都是不可逆的,因为这样的变换以后就再也找不到一个矩阵将其变换回去,这样的矩阵必然是没有逆矩阵![]() 的。
的。
详细可参考:
https://www.matongxue.com/madocs/247.html
https://www.zhihu.com/collection/200330229
三、矩阵的迹
1、矩阵的迹的基本介绍
在线性代数中,一个![]() 矩阵
矩阵![]() 的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵
的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵![]() 的迹(或迹数),一般记作
的迹(或迹数),一般记作![]() ,
,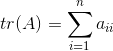 。
。
四、矩阵的特征值及特征向量
1、矩阵的特征值、特征向量的基本介绍
以下知识点来自吴传生主编的《线性代数》
1)特征值、特征向量
设![]() 是
是![]() 阶方阵,如果标量
阶方阵,如果标量![]() 和
和![]() 维非零列向量
维非零列向量![]() 使关系式
使关系式![]() 成立,则称
成立,则称![]() 是方阵
是方阵![]() 的特征值,非零列向量
的特征值,非零列向量![]() 称为
称为![]() 的对应于特征值
的对应于特征值![]() 的特征向量。
的特征向量。![]() 可改写为
可改写为![]() 。
。
这是![]()
![]() 个未知数
个未知数![]() 个方程的齐次线性方程组,它有非零解的充要条件是
个方程的齐次线性方程组,它有非零解的充要条件是![]() ,即
,即
2)特征值、特征向量的求解
求n阶方阵的特征值和特征向量的步骤如下:
-
求出n阶方阵A的特征多项式
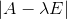
-
求出特征方程
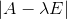 =0的全部根,
=0的全部根,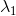 ,
, ,......,
,......,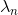 ,即为A的特征值。
,即为A的特征值。 -
把每个特征值
 代入线性方程组
代入线性方程组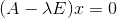 ,求出基础解系,就是A对应于
,求出基础解系,就是A对应于 的特征向量,基础解析的线性组合(零向量外)就是A对应于
的特征向量,基础解析的线性组合(零向量外)就是A对应于 的全部特征向量。
的全部特征向量。
3)特征值、特征向量的几何解释
上面我们提到,线性变换其实是施加在其基底上的变换,在以![]() 为基底的二维空间中,向量
为基底的二维空间中,向量![]() 经过矩阵
经过矩阵![]() 变换,变成
变换,变成![]() ,可以观察到,调整后
,可以观察到,调整后![]() 和
和![]() 在同一条直线上,但是
在同一条直线上,但是![]() 相对于
相对于![]() 延长了。
延长了。
此时,我们就称![]() 是
是![]() 的特征向量,而
的特征向量,而![]() 的长度是
的长度是![]() 的长度的
的长度的![]() 倍,
倍,![]() 就是特征值。
就是特征值。
所以![]() 可以理解为,
可以理解为,![]() 在
在![]() 的作用下,保持方向不变进行比例为
的作用下,保持方向不变进行比例为![]() 的伸缩。
的伸缩。
如果把矩阵看作是运动,则特征值就是运动的速度,特征向量就是运动的方向。
五、解释矩阵的特征值之和等于矩阵的迹,之积等于矩阵的行列式
1、矩阵的特征值之和等于矩阵的迹
已知求![]() 阶方阵的特征值,即求
阶方阵的特征值,即求![]() 阶方阵
阶方阵![]() 的特征多项式
的特征多项式![]() 的全部根,即求
的全部根,即求
的所有
![]() 。
。
由韦达定理可知:设,其中
![]() 代表第
代表第![]() 次项的系数,
次项的系数,![]() 代表常数项。则
代表常数项。则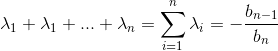 ,其中,
,其中,![]() 为
为![]() 的系数等于
的系数等于![]() (当
(当![]() 为奇数时等于-1,偶数时为1);
为奇数时等于-1,偶数时为1);![]() 为
为![]() 的系数,除了主对角元的乘积
的系数,除了主对角元的乘积![]() 的展开项之外,其他展开项的次数都小于
的展开项之外,其他展开项的次数都小于![]() ,因此
,因此![]() 次项的系数
次项的系数![]() 就是
就是 ![]() 中
中![]() 的系数,等于
的系数,等于![]() (当
(当![]() 为奇数时为负,偶数时为正),则
为奇数时为负,偶数时为正),则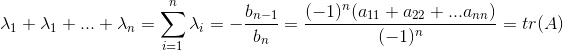 ,即矩阵的特征值之和等于矩阵的迹。
,即矩阵的特征值之和等于矩阵的迹。
2、矩阵的特征值之积等于矩阵的行列式
1)代数理解
同样根据韦达定理可知,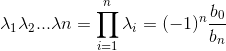 ,其中,
,其中,![]() 为
为![]() 的系数等于
的系数等于![]() (当
(当![]() 为奇数时等于-1,偶数时为1),则可化简为
为奇数时等于-1,偶数时为1),则可化简为 ,已知特征多项式
,已知特征多项式,我们令
![]() ,求得
,求得 ,
,![]() 代表
代表![]() 阶方阵
阶方阵![]() 的行列式,即
的行列式,即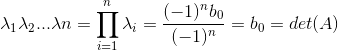 ,矩阵的特征值之积等于矩阵的行列式。
,矩阵的特征值之积等于矩阵的行列式。
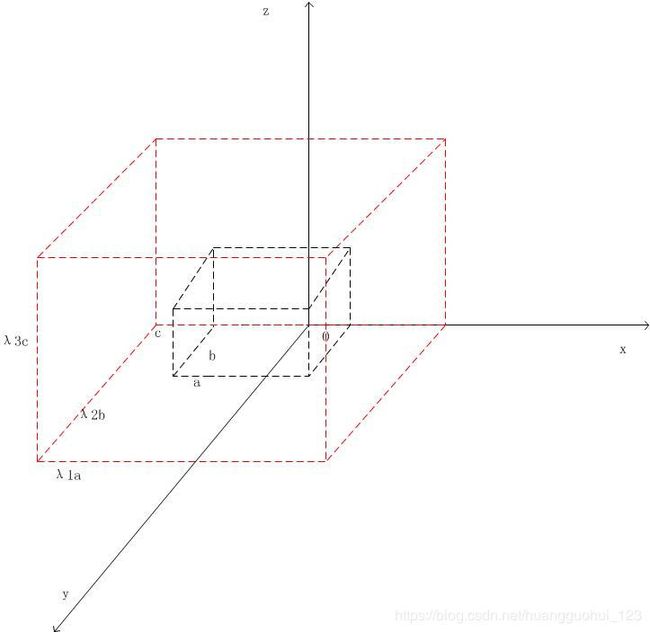
2)几何理解
特征值,理解为通过变换改变了观察者视角,由特征向量产生新的正交基,每个特征值对应着特征向量所在方向上的缩放系数,
行列式,理解为有向体积的缩放系数。
特征值在每个维度上缩放系数之乘积就是总的有向体积缩放系数。
如下图所示,原来的长方体体积![]() ,缩放之后的长方体体积等于。
,缩放之后的长方体体积等于。![]()
![]()