- 探索C#编程:高效解决N皇后问题的回溯算法实现
AitTech
算法算法c#开发语言
在C#中,回溯算法是一种通过探索所有可能的候选解来找出所有解的算法。如果候选解被确认不是一个解(或者至少不是最后一个解),回溯算法会通过在上一步进行一些变化来撤销上一步或上几步的计算,以获得新的候选解。这个过程一直进行,直到找到所有解或确定无解。回溯算法常用于解决组合问题、排列问题、子集问题、棋盘问题(如八皇后问题)、图的着色问题、旅行商问题等。示例:C#中的回溯算法实现N皇后问题N皇后问题是一个
- 力扣-N皇后问题
坚持拒绝熬夜
leetcode算法职场和发展
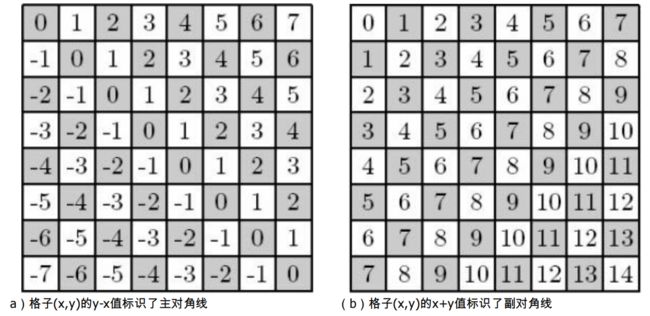
.-力扣(LeetCode)开始的思路由于n=4情况太多我们先画一下n=3的决策树可以知道皇后不能在同一行,因为我的思路是每一行每一行的填写皇后,所以不考虑行的皇后会重叠,主要考虑列的皇后会不会重叠,还有斜线的列皇后可以直接用一个数组col来标记一列中有皇后标记为true而斜线的需要一点数学功底如图可以转化成截距相等,当斜线斜率为1时,可能会有负数的情况,两边同时加上n,因为我想使用下标来标记截距
- leetcode算法题之N皇后
前端码农小黄
算法算法leetcode
N皇后也是一道很经典的问题,问题如下:题目地址按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。解法:回溯回溯是基于DFS的一种算法,它通过在解
- 九度 题目1254:N皇后问题
小白龙v5
九度C++N皇后
题目描述:N皇后问题,即在N*N的方格棋盘内放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在同一斜线上。因为皇后可以直走,横走和斜走如下图)。你的任务是,对于给定的N,求出有多少种合法的放置方法。输出N皇后问题所有不同的摆放情况个数。输入:输入包含多组测试数据。每组测试数据输入一个整数n(3usingnamespacestd;intn,sum;booldps
- 遗传算法与深度学习实战(7)——使用遗传算法解决N皇后问题
盼小辉丶
遗传算法与深度学习实战深度学习DEAP遗传算法
遗传算法与深度学习实战(7)——使用遗传算法解决N皇后问题0.前言1.N皇后问题2.解的表示3.遗传算法解决N皇后问题小结系列链接0.前言进化算法(EvolutionaryAlgorithm,EA)和遗传算法(GeneticAlgorithms,GA)已成功解决了许多复杂的设计和布局问题,部分原因是它们采用了受控随机元素的搜索。这通常使得使用EA或GA设计的系统能够超越我们的理解进行创新。在本节中
- leetcode51 N皇后问题
浦东新村轱天乐
leetcode算法数据结构
https://programmercarl.com/0051.N%E7%9A%87%E5%90%8E.html代码随想录讲的很清楚。回溯法从上到下按行搜索,因此back_tracking(chessboard,row+1)其参数为row+1判断该位置是否符合终止条件是i==nclassSolution{public://vectorpath_;vector>res_;boolvalid(vect
- 【leetcode题解C++】51.N皇后 and 76.最小覆盖子串
WISHMELUCK1'
leetcodeleetcodec++算法
51.N皇后按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。示例1:输入:n=4输出:[[".Q..","...Q","Q...","..Q.
- C++ dfs状态的表示(五十三)【第十三篇】
我家小白小花儿
C++深度优先算法
今天我们将来求解N皇后问题。1.N皇后问题N皇后问题是一个经典的问题,在一个N×N的棋盘上放置N个皇后,每行刚好放置一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。上图就是一个合法的8皇后的解。N皇后问题是指:计算一共有多少种合法的方法放置N个皇后。很显然,我们依然会用dfs来求解N皇后问题,我们的搜索策略如下。从第0列开始,我们依次给每一列放置一个皇后,对于一个确定的列,
- day30 n皇后
NHCyrus
算法
day29回溯N皇后题目链接:N皇后题目描述按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中‘Q’和‘.’分别代表了皇后和空位。?解答classSolution{List>res
- LeetCode|Python|400题分类刷题记录——递归
ClaraR
pythonleetcodepythonleetcode
递归/DFS/BFS在不断更新中...51.N皇后n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。示例1:输入:n=4输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...",
- 【LeetCode】51. N 皇后(困难)——代码随想录算法训练营Day30
晴雪月乔
代码随想录算法训练营#LeetCode回溯法算法代码随想录算法训练营leetcode回溯法
题目链接:51.N皇后题目描述按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。示例1:输入:n=4输出:[[".Q..","...Q","Q.
- leetcode:51. N皇后
暮色恍然
LeetCodeLeetCode
题目:n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。上图为8皇后问题的一种解法。给定一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个明确的n皇后问题的棋子放置方案,该方案中‘Q’和‘.’分别代表了皇后和空位。示例:输入:4输出:[[".Q…",//解法1“…Q”,“Q…”,“…Q.”],["…Q.",//解法2“Q…”,“…Q”,“.Q…”
- leetcode:51. N 皇后
uncle_ll
编程练习-Leetcodeleetcode八皇后N皇后回溯算法训练
51.N皇后来源:力扣(LeetCode)链接:https://leetcode.cn/problems/n-queens/按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中‘Q’
- 回溯算法——n皇后问题
桑稚远方~
算法
什么是回溯算法?回溯法,⼀般可以解决如下几种问题:组合问题、排列问题、子集问题、棋盘问题等问题;n皇后问题就是其中的棋盘问题;回溯法要解决的问题都可以抽象为树形结构,可以理解为N叉树;回溯法使用递归,在一个集合中递归找子集,集合的大小就可以理解为需要递归的层;并且使用递归就要有终止条件,不然就在函数体中出不来,会出错。所以这颗N叉树就是有限的;回溯算法的流程:1.回溯函数进入的参数以及返回值;就是
- java写n皇后问题回溯法_回溯算法:N皇后问题
知乎电影
java写n皇后问题回溯法
❞如果对回溯法理论还不清楚的同学,可以先看这个视频:n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互***。上图为8皇后问题的一种解法。给定一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个明确的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。示例:输入:4输出:[[".Q..",//解法1"...Q","Q...","..Q.
- python中级篇1:n皇后问题(回溯算法)
浪矢秀一
算法python
hello!大家好,我是浪矢秀一。最近经历了许多事情,终于是恢复1次更新了。那么今天呢,我们来学习中级篇,需要学过不少python知识的人来学习。好了,废话不多说,我们进入今天的课程!n皇后问题题目在1个n*n的国际象棋棋盘上,放置n个皇后,要求:同1行、同1列、同1斜线上只能有1个皇后。题目分析既然是有很多行,分别满足不同条件,那么我们可以进行枚举每行,再枚举每列。但是,如果1行都不满足的话,就
- 回溯算法:N皇后问题
DevDiary
算法回溯算法N皇后问题
N皇后问题是一个经典的回溯算法应用问题,要求在一个N×N的棋盘上放置N个皇后,使得它们互不攻击。即任何两个皇后都不能位于同一行、同一列或同一对角线上。这个问题可以通过回溯算法来解决,下面详细讲解这个问题的解法。解题思路逐行放置:一种有效的解决方案是逐行放置皇后,这样可以保证每行只有一个皇后。检查冲突:放置每个皇后时,需要检查当前放置的皇后是否与已放置的皇后冲突(即检查列和对角线)。回溯:如果当前行
- 网课:N皇后问题——牛客(题解和疑问)
2301_80718054
算法dfs
题目描述给出一个n×nn\timesnn×n的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。输入描述:一行,一个整数n(1≤n≤12)n(1\len\le12)n(1≤n≤12),表示棋盘的大小。输出描述:输出一行一个整数,表示总共有多少种摆放皇后的方案,使得它们两两不能
- 第三十天| 51. N皇后
%dionysus%
代码随想录算法训练营算法leetcode
Leetcode51.N皇后题目链接:51N皇后题干:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。思考:回溯法。先定义结果集result,
- 常用算法模板之图论(持续更新)
荔枝还冷静
算法图论深度优先数据结构c++图搜索算法
DFSDFS的结果就是一颗搜索树,只不过每次只记录眼前的分支,然后通过栈回溯到上一个节点再往下朝另一个方向搜索,绘出所有轨迹就是一棵搜索树。排列数字问题#includeusingnamespacestd;constintN=8;intn,path[N];boolst[N];voiddfs(intu){if(u==n){for(inti=0;i>n;dfs(0);return0;}经典N皇后问题#i
- 二道经典OJ题带你入门回溯剪枝算法
烟雨长虹,孤鹜齐飞
C++剪枝算法c语言C++回溯DFS
风起于青萍之末浪成于微澜之间个人主页个人专栏前期回顾-环形链表目录回溯算法的简介N皇后问题思路代码测试N皇后思路判断一竖列是否有皇后判断对角线是否有皇后代码测试回溯算法的简介回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和DFS混在一起回溯的介绍:在搜索解空间时会采用尝试与回退的策略回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,
- 【力扣 51】N 皇后(回溯+剪枝+深度优先搜索)
HEX9CF
AlgorithmProblemsleetcode剪枝深度优先
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中‘Q’和‘.’分别代表了皇后和空位。示例1:输入:n=4输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q
- U402491 N皇后问题
SYZ0610
算法
题目传送门题目描述一个n×n的国际象棋棋盘,有n个皇后被放置在棋盘上,使得每两个皇后之间不能直接吃掉对方(每行、每列和两个对角线有且只有一个皇后)。输入格式一个n,代表棋盘大小(n*n)和皇后个数输出格式按给定顺序和格式输出所有N皇后问题的解输入输出样例输入#18输出#1No.1Q...........Q..........Q.....Q....Q...........Q..Q.........Q
- n皇后问题(DFS)
自律的kkk
算法数据结构
原题详细如下:n−皇后问题是指将n个皇后放在n×n的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。现在给定整数n,请你输出所有的满足条件的棋子摆法。输入格式共一行,包含整数n。输出格式每个解决方案占n行,每行输出一个长度为n的字符串,用来表示完整的棋盘状态。其中.表示某一个位置的方格状态为空,Q表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一
- 【算法很美】深入递归 (下)深度优先搜索DFS问题
小易I
算法学习java算法蓝桥杯数据结构dfs
深搜、回溯、剪枝深度优先搜索DFS2.1无死角搜索I数独游戏部分和水洼数目2.2回溯和剪枝n皇后问题素数环困难的串小结一些使用2.1无死角搜索I数独游戏你一定听说过“数独”游戏。如下图所示,玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个同色九宫内的数字均含1-9,不重复。数独的答案都是唯一的,所以,多个解也称为无解。本图的数字据说是芬兰数学家花了3个月的
- Leetcode-3--递归、DFS、回溯
NKidult
Leetcode
Leetcode--回溯、进制运算递归24两两交换链表143重排链表98验证二叉搜索树1796不同的二叉搜索树二叉树展开成链表回溯22括号生成39组合总和40组合总和216组合总和46排列47全排列⭐️剑指offer字符串排列131分割回文串78子集416.分割等和子集N皇后问题面试题08.08.有重复字符串的排列组合硬币兑换74单词搜索剑指Offer55-II.平衡二叉树面试题08.08.有重复
- 力扣labuladong一刷day70天回溯大集合
当年拼却醉颜红
力扣算法题leetcode算法职场和发展
力扣labuladong一刷day70天回溯大集合文章目录力扣labuladong一刷day70天回溯大集合一、51.N皇后二、37.解数独一、51.N皇后题目链接:https://leetcode.cn/problems/n-queens/思路:n皇后问题,利用回溯来搜索正确答案,每次向下递归都是新的一层,进入递归之前都会做是否可以作为皇后的判断。classSolution{List>array
- 2021-02-16:n皇后问题。给定一个整数n,返回n皇后的摆法有多少种?
福大大架构师每日一题
福哥答案2021-02-16:自然智慧即可。1.普通递归。有代码。需要判断同列和斜线。2.位运算递归。有代码。3.我的递归。有代码。只需要判断斜线。代码用golang编写,代码如下:packagemainimport("fmt""time")funcmain(){n:=12fmt.Println(n,"皇后问题")fmt.Println("------")now:=time.Now()fmt.Pr
- 回溯算法--LeetCode-51 N皇后
DY_HM
Leetcoden皇后回溯LeetCodeJava
题目链接:https://leetcode-cn.com/problems/n-queens/n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给定一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个明确的n皇后问题的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。示例:输入:4输出:[[".Q..",//解法1"...Q","Q..."
- LeetCode刷题-----N皇后问题
代码改变世界~
LeetCodeleetcode算法数据结构
LeetCode刷题-----N皇后问题(回溯法)51.N皇后题目描述:n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的n皇后问题的解决方案。每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中‘Q’和‘.’分别代表了皇后和空位。思路:枚举每一行,每一列,判断是否放的下classSolution{List>list=newL
- 开发者关心的那些事
圣子足道
ios游戏编程apple支付
我要在app里添加IAP,必须要注册自己的产品标识符(product identifiers)。产品标识符是什么?
产品标识符(Product Identifiers)是一串字符串,它用来识别你在应用内贩卖的每件商品。App Store用产品标识符来检索产品信息,标识符只能包含大小写字母(A-Z)、数字(0-9)、下划线(-)、以及圆点(.)。你可以任意排列这些元素,但我们建议你创建标识符时使用
- 负载均衡器技术Nginx和F5的优缺点对比
bijian1013
nginxF5
对于数据流量过大的网络中,往往单一设备无法承担,需要多台设备进行数据分流,而负载均衡器就是用来将数据分流到多台设备的一个转发器。
目前有许多不同的负载均衡技术用以满足不同的应用需求,如软/硬件负载均衡、本地/全局负载均衡、更高
- LeetCode[Math] - #9 Palindrome Number
Cwind
javaAlgorithm题解LeetCodeMath
原题链接:#9 Palindrome Number
要求:
判断一个整数是否是回文数,不要使用额外的存储空间
难度:简单
分析:
题目限制不允许使用额外的存储空间应指不允许使用O(n)的内存空间,O(1)的内存用于存储中间结果是可以接受的。于是考虑将该整型数反转,然后与原数字进行比较。
注:没有看到有关负数是否可以是回文数的明确结论,例如
- 画图板的基本实现
15700786134
画图板
要实现画图板的基本功能,除了在qq登陆界面中用到的组件和方法外,还需要添加鼠标监听器,和接口实现。
首先,需要显示一个JFrame界面:
public class DrameFrame extends JFrame { //显示
- linux的ps命令
被触发
linux
Linux中的ps命令是Process Status的缩写。ps命令用来列出系统中当前运行的那些进程。ps命令列出的是当前那些进程的快照,就是执行ps命令的那个时刻的那些进程,如果想要动态的显示进程信息,就可以使用top命令。
要对进程进行监测和控制,首先必须要了解当前进程的情况,也就是需要查看当前进程,而 ps 命令就是最基本同时也是非常强大的进程查看命令。使用该命令可以确定有哪些进程正在运行
- Android 音乐播放器 下一曲 连续跳几首歌
肆无忌惮_
android
最近在写安卓音乐播放器的时候遇到个问题。在MediaPlayer播放结束时会回调
player.setOnCompletionListener(new OnCompletionListener() {
@Override
public void onCompletion(MediaPlayer mp) {
mp.reset();
Log.i("H
- java导出txt文件的例子
知了ing
javaservlet
代码很简单就一个servlet,如下:
package com.eastcom.servlet;
import java.io.BufferedOutputStream;
import java.io.IOException;
import java.net.URLEncoder;
import java.sql.Connection;
import java.sql.Resu
- Scala stack试玩, 提高第三方依赖下载速度
矮蛋蛋
scalasbt
原文地址:
http://segmentfault.com/a/1190000002894524
sbt下载速度实在是惨不忍睹, 需要做些配置优化
下载typesafe离线包, 保存为ivy本地库
wget http://downloads.typesafe.com/typesafe-activator/1.3.4/typesafe-activator-1.3.4.zip
解压r
- phantomjs安装(linux,附带环境变量设置) ,以及casperjs安装。
alleni123
linuxspider
1. 首先从官网
http://phantomjs.org/下载phantomjs压缩包,解压缩到/root/phantomjs文件夹。
2. 安装依赖
sudo yum install fontconfig freetype libfreetype.so.6 libfontconfig.so.1 libstdc++.so.6
3. 配置环境变量
vi /etc/profil
- JAVA IO FileInputStream和FileOutputStream,字节流的打包输出
百合不是茶
java核心思想JAVA IO操作字节流
在程序设计语言中,数据的保存是基本,如果某程序语言不能保存数据那么该语言是不可能存在的,JAVA是当今最流行的面向对象设计语言之一,在保存数据中也有自己独特的一面,字节流和字符流
1,字节流是由字节构成的,字符流是由字符构成的 字节流和字符流都是继承的InputStream和OutPutStream ,java中两种最基本的就是字节流和字符流
类 FileInputStream
- Spring基础实例(依赖注入和控制反转)
bijian1013
spring
前提条件:在http://www.springsource.org/download网站上下载Spring框架,并将spring.jar、log4j-1.2.15.jar、commons-logging.jar加载至工程1.武器接口
package com.bijian.spring.base3;
public interface Weapon {
void kil
- HR看重的十大技能
bijian1013
提升能力HR成长
一个人掌握何种技能取决于他的兴趣、能力和聪明程度,也取决于他所能支配的资源以及制定的事业目标,拥有过硬技能的人有更多的工作机会。但是,由于经济发展前景不确定,掌握对你的事业有所帮助的技能显得尤为重要。以下是最受雇主欢迎的十种技能。 一、解决问题的能力 每天,我们都要在生活和工作中解决一些综合性的问题。那些能够发现问题、解决问题并迅速作出有效决
- 【Thrift一】Thrift编译安装
bit1129
thrift
什么是Thrift
The Apache Thrift software framework, for scalable cross-language services development, combines a software stack with a code generation engine to build services that work efficiently and s
- 【Avro三】Hadoop MapReduce读写Avro文件
bit1129
mapreduce
Avro是Doug Cutting(此人绝对是神一般的存在)牵头开发的。 开发之初就是围绕着完善Hadoop生态系统的数据处理而开展的(使用Avro作为Hadoop MapReduce需要处理数据序列化和反序列化的场景),因此Hadoop MapReduce集成Avro也就是自然而然的事情。
这个例子是一个简单的Hadoop MapReduce读取Avro格式的源文件进行计数统计,然后将计算结果
- nginx定制500,502,503,504页面
ronin47
nginx 错误显示
server {
listen 80;
error_page 500/500.html;
error_page 502/502.html;
error_page 503/503.html;
error_page 504/504.html;
location /test {return502;}}
配置很简单,和配
- java-1.二叉查找树转为双向链表
bylijinnan
二叉查找树
import java.util.ArrayList;
import java.util.List;
public class BSTreeToLinkedList {
/*
把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ \
6 14
/ \
- Netty源码学习-HTTP-tunnel
bylijinnan
javanetty
Netty关于HTTP tunnel的说明:
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/socket/http/package-summary.html#package_description
这个说明有点太简略了
一个完整的例子在这里:
https://github.com/bylijinnan
- JSONUtil.serialize(map)和JSON.toJSONString(map)的区别
coder_xpf
jqueryjsonmapval()
JSONUtil.serialize(map)和JSON.toJSONString(map)的区别
数据库查询出来的map有一个字段为空
通过System.out.println()输出 JSONUtil.serialize(map): {"one":"1","two":"nul
- Hibernate缓存总结
cuishikuan
开源sshjavawebhibernate缓存三大框架
一、为什么要用Hibernate缓存?
Hibernate是一个持久层框架,经常访问物理数据库。
为了降低应用程序对物理数据源访问的频次,从而提高应用程序的运行性能。
缓存内的数据是对物理数据源中的数据的复制,应用程序在运行时从缓存读写数据,在特定的时刻或事件会同步缓存和物理数据源的数据。
二、Hibernate缓存原理是怎样的?
Hibernate缓存包括两大类:Hib
- CentOs6
dalan_123
centos
首先su - 切换到root下面1、首先要先安装GCC GCC-C++ Openssl等以来模块:yum -y install make gcc gcc-c++ kernel-devel m4 ncurses-devel openssl-devel2、再安装ncurses模块yum -y install ncurses-develyum install ncurses-devel3、下载Erang
- 10款用 jquery 实现滚动条至页面底端自动加载数据效果
dcj3sjt126com
JavaScript
无限滚动自动翻页可以说是web2.0时代的一项堪称伟大的技术,它让我们在浏览页面的时候只需要把滚动条拉到网页底部就能自动显示下一页的结果,改变了一直以来只能通过点击下一页来翻页这种常规做法。
无限滚动自动翻页技术的鼻祖是微博的先驱:推特(twitter),后来必应图片搜索、谷歌图片搜索、google reader、箱包批发网等纷纷抄袭了这一项技术,于是靠滚动浏览器滚动条
- ImageButton去边框&Button或者ImageButton的背景透明
dcj3sjt126com
imagebutton
在ImageButton中载入图片后,很多人会觉得有图片周围的白边会影响到美观,其实解决这个问题有两种方法
一种方法是将ImageButton的背景改为所需要的图片。如:android:background="@drawable/XXX"
第二种方法就是将ImageButton背景改为透明,这个方法更常用
在XML里;
<ImageBut
- JSP之c:foreach
eksliang
jspforearch
原文出自:http://www.cnblogs.com/draem0507/archive/2012/09/24/2699745.html
<c:forEach>标签用于通用数据循环,它有以下属性 属 性 描 述 是否必须 缺省值 items 进行循环的项目 否 无 begin 开始条件 否 0 end 结束条件 否 集合中的最后一个项目 step 步长 否 1
- Android实现主动连接蓝牙耳机
gqdy365
android
在Android程序中可以实现自动扫描蓝牙、配对蓝牙、建立数据通道。蓝牙分不同类型,这篇文字只讨论如何与蓝牙耳机连接。
大致可以分三步:
一、扫描蓝牙设备:
1、注册并监听广播:
BluetoothAdapter.ACTION_DISCOVERY_STARTED
BluetoothDevice.ACTION_FOUND
BluetoothAdapter.ACTION_DIS
- android学习轨迹之四:org.json.JSONException: No value for
hyz301
json
org.json.JSONException: No value for items
在JSON解析中会遇到一种错误,很常见的错误
06-21 12:19:08.714 2098-2127/com.jikexueyuan.secret I/System.out﹕ Result:{"status":1,"page":1,&
- 干货分享:从零开始学编程 系列汇总
justjavac
编程
程序员总爱重新发明轮子,于是做了要给轮子汇总。
从零开始写个编译器吧系列 (知乎专栏)
从零开始写一个简单的操作系统 (伯乐在线)
从零开始写JavaScript框架 (图灵社区)
从零开始写jQuery框架 (蓝色理想 )
从零开始nodejs系列文章 (粉丝日志)
从零开始编写网络游戏
- jquery-autocomplete 使用手册
macroli
jqueryAjax脚本
jquery-autocomplete学习
一、用前必备
官方网站:http://bassistance.de/jquery-plugins/jquery-plugin-autocomplete/
当前版本:1.1
需要JQuery版本:1.2.6
二、使用
<script src="./jquery-1.3.2.js" type="text/ja
- PLSQL-Developer或者Navicat等工具连接远程oracle数据库的详细配置以及数据库编码的修改
超声波
oracleplsql
在服务器上将Oracle安装好之后接下来要做的就是通过本地机器来远程连接服务器端的oracle数据库,常用的客户端连接工具就是PLSQL-Developer或者Navicat这些工具了。刚开始也是各种报错,什么TNS:no listener;TNS:lost connection;TNS:target hosts...花了一天的时间终于让PLSQL-Developer和Navicat等这些客户
- 数据仓库数据模型之:极限存储--历史拉链表
superlxw1234
极限存储数据仓库数据模型拉链历史表
在数据仓库的数据模型设计过程中,经常会遇到这样的需求:
1. 数据量比较大; 2. 表中的部分字段会被update,如用户的地址,产品的描述信息,订单的状态等等; 3. 需要查看某一个时间点或者时间段的历史快照信息,比如,查看某一个订单在历史某一个时间点的状态, 比如,查看某一个用户在过去某一段时间内,更新过几次等等; 4. 变化的比例和频率不是很大,比如,总共有10
- 10点睛Spring MVC4.1-全局异常处理
wiselyman
spring mvc
10.1 全局异常处理
使用@ControllerAdvice注解来实现全局异常处理;
使用@ControllerAdvice的属性缩小处理范围
10.2 演示
演示控制器
package com.wisely.web;
import org.springframework.stereotype.Controller;
import org.spring