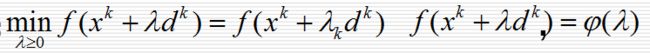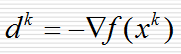【MATLAB】最速下降方法
最速下降法
定义:沿负梯度方向进行搜索的算法(负梯度方向为最速下降方向)
优化问题:
算法流程
1.取 x0,令k=0 ;
2.求 xk 处 f(x) 的一个下降方向 dk ;
否则,转步骤2;
例题求解:
1.实现最速梯度下降法MATLAB关键几点
1)建立符号表达式表达函数
建立函数表达式可以使用matlab中的符号变量和符号表达式功能。
如下示例,利用三种方式构造函数表达式x^2+x-2,并将其转换为多项式,求其根。
%构成符号表达式方法一:
fx = sym('x^2+x-2');% 利用sym('符号字符串')构成符号表达式
ployx = sym2poly(fx)% 转换成多项式
roots(ployx);% 原符号表达式转换为多项式后求根
ans =
-2
1
%构成符号表达式方法二:
syms x;%利用syms定义符号变量
fx = x^2+x-2;%利用已定义的符号变量组成符号表达式
polyx = sym2poly(fx);
roots(polyx)
ans =
-2
1
%构成符号表达式方法三:
fx = 'x^2+x-2';%利用单引号建立符号表达式,与之前定义有区别,实质上定义的是char类型
fx = sym(fx);%转换为真正意义的符号表达式
polyx = sym2poly(fx);
roots(polyx)
ans =
-2
1
注意两点:
a. 利用单引号生成的符号表达式建立的并不是真正意义上的符号表达式(sym类型),就是一个普通的字符串(char类型)。
如以下示例:
>> fx = 'x^2+x-2';
>> fy = sym('y^2+y-2');
>> whos
Name Size Bytes Class Attributes
fx 1x7 14 char
fy 1x1 60 sym
我们可以发现,利用单引号创建的符号表达式存贮为char类型,而不是sym类型。
因此使用单引号创建符号表达式时注意作用在其上函数的影响,要将其转换为真正符号表达式,如:
>> y = 'x^3+x^5'
y =
x^3+x^5
>> diff(y) %计算结果明显错误
ans =
-26 -43 -8 77 -26 -41
>> diff(sym(y)) %先转换为符号表达式,再求微分,结果正确
ans =
5*x^4 + 3*x^2
b.符号表达式计算的结果必要时要转换为数值类型
例如,
>> syms x;
>> fx = x^2+x-2;
>> ret = solve(fx)
ret =
1
-2
>> whos ret
Name Size Bytes Class Attributes
ret 2x1 60 sym
>> ret = double(ret);%利用double函数将sym类型转换为数值类型
>> whos ret
Name Size Bytes Class Attributes
ret 2x1 16 double
这里利用solve函数返回的根,是符号变量,将它直接与数值类型计算时,将产生错误,利用double将其转换为数值类型。
2)求解函数的梯度,从而获取搜索方向
求解函数梯度需要利用gradient函数,代入某个位置,求具体点的梯度需要使用subs函数,示例如下:
>> syms x1 x2;
X = [x1;x2];
fx = x1-x2+2*x1^2+2*x1*x2+x2^2;
>> gradx = gradient(fx,X) %计算梯度函数
gradx =
4*x1 + 2*x2 + 1
2*x1 + 2*x2 - 1
>> ret = subs(gradx,X,[1 2]) %计算在点(1,2)处梯度
ret =
9
5
3)寻找最佳步长
最佳步长,需要求解方程: step* = min f(x[k]+step*d[k]),其中x[k]表示当前位置,step表示步长,d[k]表示当前搜索方向,step*表示所求去的理想步长。
理想步长的求解,就是求解使上述方程取最小值的步长,可以通过求导函数的实数零点来获取。
这个地方需要使用符号变量和符号表达式的技巧,具体可参见代码清单2-2部分的函数getNextStep(fx,var,xk,dk) 。
4)精度控制问题
一方面利用精度控制迭代的过程的终止,另一方面如果你想观察计算过程也要控制精度。
如果没有控制精度,很有可能把正确的计算结果当成错误的结果。例如:
>> ft = sym('(44*t-2)^4+(92*t-6)^2');
>> ft_diff = diff(ft);%求导数
>> roots = solve(ft_diff) %求导数方程的根
roots =
((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3) - 529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + 1/22
(3^(1/2)*(529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3))*i)/2 + 529/(2811072*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) - ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)/2 + 1/22
529/(2811072*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) - (3^(1/2)*(529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3))*i)/2 - ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)/2 + 1/22
>> roots = vpa(solve(ft_diff)) %控制位默认精度显示
roots =
0.0615348488488
0.0374143937574 + 0.0363735994416*i
0.0374143937574 - 0.0363735994416*i
>> size(roots)
ans =
3 1
代码实现:
后续补齐.........................