Stereo Processing by Semiglobal Matching and Mutual Information

SGM中文名称“半全局匹配”，顾名思义，其介于局部算法和全局算法之间，所谓半全局指的是算法既没有只考虑像素的局部区域，也没有考虑所有的像素点。例如，BM计算某一点视差的时候，往往根据目标像素周围的矩形区域进行代价聚合计算；DoubleBP在计算目的像素视差的时候，考虑的则是图像所有的像素点。抛开具体的方法不说，SGM中考虑到的只有非遮挡点，这正是定义为半全局的原因。这篇文章主要涉及三个部分：分层互信息的代价计算+基于动态规划的代价聚合+视差计算和细化

1.分层互信息代价计算

其中，互信息的前两项是图像的熵，最后一项叫做联合熵，联合熵是熵的变种，其依赖的自然是联合概率分布（熵依赖的是概率分布），联合熵的公式如下所示：

图像的概率分布P是图像的灰度直方图。图像的灰度值是0~255，每个灰度值对应的像素个数除以图像像素个数就是该灰度值对应的概率，单幅图像的概率密度是一维的，那么自然地，两幅图像的联合概率密度就是二维的，它的定义域取值就是（0，0）~（255，255），公式如下所示：

其中，（i，k）指的是像素灰度值对，I1和I2分别代表了左图和矫正之后的右图，p代表像素点，n代表着像素的总数，公式的含义是统计不同灰度值对的个数并归一化。因此，两幅图像对应的概率分布可以用一幅图表示，这幅图的大小一定是256*256。
联合熵的定义，在这里作者引用了其他文献的研究成果，直接用泰勒展开近似联合熵为像素和的形式，如下所示：

其中，作者称h为数据项，注意看它的自变量是像素灰度值，所以可以事先建立一个查表，将每个灰度值对的h值都保存下来（一共有256*256），那么联合熵的计算速度就会很快，h的计算公式如下所示：

与高斯核函数进行卷积在这里起到平滑的作用。概率P是对所有的corresponding points（假设有n个）构成灰度值对的统计，可以用联合直方图计算。如果两个图像匹配得越好，计算得H就会非常小，加负号后就是非常大，也就是互信息会越大。

本来熵和联合熵的计算方法不同，但是由于遮挡点的问题，将二者都设置为相同，都采用泰勒近似的方式。具体来说，图像的熵是基于图像的概率分布来计算的，但由于遮挡点的存在，有些像素根本就不会有匹配点，如果也将这样的像素考虑在内恐怕不合适，别忘了我们的目的是令能够匹配的点尽量匹配，不能匹配的点我们根本就没必要让它们匹配，于是将目光放在了联合熵的定义上，联合熵是基于联合概率分布的，其基于的点可以保证都是匹配点，这样的概率公式如下所示：

基于这样的概率分布得到的图像熵公式如下所示：

最后，作者采用分层互信息（HMI）进行代价匹配计算，由于概率分布图和图像大小无关（一直都是256*256），所以可以采用分层计算的方式来加速（反正不同层都是256*256），每一层的计算对应一次迭代，首次迭代需要基于随机生成的视差图对右图进行warp，并且由于像素个数很多，随机生成的个别错误可以被容忍，warp之后的右图和左图的匹配程度还是会比较高，迭代次数也相对较低，这也是SGM的一大优点。

由于单次迭代的时间复杂度是O(WHD)，每次下采样都会令三个参数同时减半，所以上次迭代将会是当前迭代速度的1/8，假设我们有4次迭代，那么相比较于BT算法，只比它慢了14%，注意，算法首次迭代使用的是最小的视差图，并且乘以3的原因是随机生成的视差图十分不靠谱，需要反复迭代3次才能得到同样分辨率下的靠谱视差图，然后再参与后续高分辨率的计算。

2.基于动态规划的代价聚合

SGM的代价聚合是为了优化一个能量函数，这和一般的全局算法一样，如何利用优化算法求解复杂的能量函数才是重中之重，其能量函数如下所示：

其中，C(p, Dp)代表的就是基于互信息的代价计算项，后面两项指的是当前像素p和其邻域内所有像素q之间的约束，如果q和p的视差只差了1，那么惩罚P1，如果大于1，那么惩罚P2。

• 假如不考虑像素之间的制约关系，不假设领域内像素应该具有相同的视差值，那么最小化E(D)就是最小化每一个C，这样的视差图效果很差，因为图像总会收到光照，噪声等因素的影响，最小的代价对应的视差往往是“假的”，并且这样做全然不考虑相邻之间的像素关系，例如，一个桌面的视差明显应该相同，但是可能由于倾斜光照的影响，每个像素的最小代价往往会不同，所以看起来就会乱七八糟，东一块西一块。这就是加上约束的目的。
• 添加两个正则化项一方面是为了保证视差图平滑，另一方面为了保持边缘（保持边缘一直没想明白为什么？）。惩罚的越大，说明越不想看到这种情况发生，具体来说，如果q和p之间的视差有所差异但又不大，那么就要付出代价，你不是想最小化能量函数么？那么二者都要小，如果没有第二项，那么求出来的视差图将会有明显的锯齿现象，如果只有第三项，那么求出来的视差图边缘部分将会得到保持，但由于没有对相差为1的相邻像素进行惩罚，物体内部很可能出现一个“斜面”。

怎么利用动态规划来求解E，其实这个求解问题是NP完全问题，想在2D图像上直接利用动态规划求解是不可能的，只有沿着每一行或者每一列求解才能够满足多项式时间（又叫做扫描线优化），但是这里问题来了，如果我们只沿着每一行求解，那么行间的约束完全考虑不到，q是p的领域的点其实这个时候被弱化到了q是p的左侧点或者右侧点，这样的求优效果肯定很差。于是，大招来了！！我们索性不要只沿着横或者纵来进行优化，而是沿着一圈8个或者16个方向进行优化。

求解过程:


其中，P1是对物体不平整表面的适应，P2是对灰度不连续（可能是多个物体）的适应，这样可以起到平滑视差图的效果。最后一项减去r方向在前一个像素点的L，添加这一项并不会改变最终视差图结果，只是为了限制L（不断增长至极大值）的规模。
求解方法：假设每个像素的disparity只和其左边的像素相关，有如下公式：

r指某个指向当前像素p的方向，在此可以理解为像素p左边的相邻像素。
Lr(p, d) 表示沿着当前方向（即从左向右），当目前像素p的disparity取值为d时，其最小cost值。

这个最小值是从4种可能的候选值中选取的最小值：

1.前一个像素（左相邻像素）disparity取值为d时，其最小的cost值。

2.前一个像素（左相邻像素）disparity取值为d-1时，其最小的cost值+惩罚系数P1。

3.前一个像素（左相邻像素）disparity取值为d+1时，其最小的cost值+惩罚系数P1。

4.前一个像素（左相邻像素）disparity取值为其他时，其最小的cost值+惩罚系数P2。

另外，当前像素p的cost值还需要减去前一个像素取不同disparity值时最小的cost。这是因为Lr(p, d)是会随着当前像素的右移不停增长的，为了防止数值溢出，所以要让它维持在一个较小的数值。

在代价聚合阶段，作者交换匹配图与待测图位置，可以得到两个视差图Db和Dm，然后用一致性检测保证一对一的映射，否则该点作为黑点（255）。

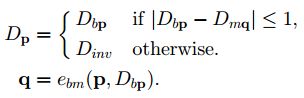
参考：
http://blog.csdn.net/wsj998689aa/article/details/49464017
http://blog.csdn.net/lcc921528642/article/details/42550819