线性代数(17)——坐标转换
坐标转换
- 空间的基与坐标系
- 任意坐标系与标准坐标系之间的转换
- 任意坐标系之间的转换
- 标准单位矩阵作为桥梁
- 结论验证
- 不使用单位坐标系为桥梁的情况
空间的基与坐标系
坐标系是理解空间的基的一个视角,如果只到了一个坐标系也相当于知道了空间中的一组基向量。
之前的笔记中提及过,对于同一个点,在不同的基向量构成的坐标系中,其表示形式是不同的,如下图所示,
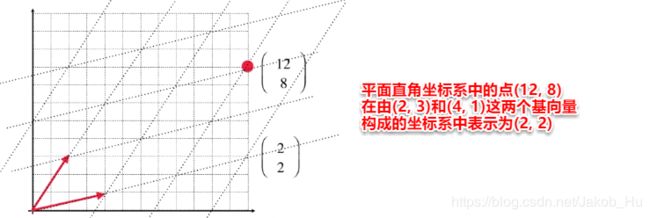
故对空间的基和坐标系之间的关系作出如下定义,
如果给定向量空间 V V V在的一组基 B = { b 1 ⃗ , b 2 ⃗ , b 3 ⃗ , . . . b n ⃗ } B=\{\vec{b_1},\vec{b_2},\vec{b_3},...\vec{b_n}\} B={b1,b2,b3,...bn}以及 V V V中的一个向量 x ⃗ \vec{x} x,则 x ⃗ \vec{x} x一定可以被这组基线性表示。假设: x ⃗ = c 1 b 1 ⃗ + c 2 b 2 ⃗ + c 3 b 3 ⃗ + . . . + c n b n ⃗ \vec{x}=c_1\vec{b_1}+c_2\vec{b_2}+c_3\vec{b_3}+...+c_n\vec{b_n} x=c1b1+c2b2+c3b3+...+cnbn,则称 x ⃗ \vec{x} x在这组基 B B B下的坐标为 ( c 1 c 2 c 3 . . . c n ) T \begin{pmatrix}c_1&c_2&c_3&...&c_n\end{pmatrix}^T (c1c2c3...cn)T。记为 [ x ⃗ ] B [\vec{x}]_B [x]B。
以上图 ( 12 , 8 ) (12,8) (12,8)为例,
ϵ = { e 1 ⃗ , e 2 ⃗ } ⟹ B = { u ⃗ , v ⃗ } x ⃗ = 12 e 1 ⃗ + 8 e 2 ⃗ ⟹ x ⃗ = 2 u ⃗ + 2 v ⃗ [ x ⃗ ] ϵ = ( 12 8 ) ⟹ [ x ⃗ ] B = ( 2 2 ) \epsilon=\{\vec{e_1} ,\vec{e_2}\}\Longrightarrow B=\{\vec{u}, \vec{v}\}\\\vec{x}=12\vec{e_1}+8\vec{e_2}\Longrightarrow \vec{x}=2\vec{u}+2\vec{v}\\ [\vec{x}]_{\epsilon}=\begin{pmatrix}12\\8\end{pmatrix}\Longrightarrow [\vec{x}]_B=\begin{pmatrix}2\\2\end{pmatrix} ϵ={e1,e2}⟹B={u,v}x=12e1+8e2⟹x=2u+2v[x]ϵ=(128)⟹[x]B=(22)
一般认为的坐标系空间就是由 ϵ \epsilon ϵ构成的标准坐标系, ϵ \epsilon ϵ所对应的即称为标准基。一定注意区分标准基和标准正交基,前者的范围更小。
| 基( n n n维度空间) | 说明 |
|---|---|
| 标准基 | 有且只有一组,是由1个1和 n − 1 n-1 n−1个0通过不同的排列得到的 |
| 标准正交基 | 有无数组的 |
任意坐标系与标准坐标系之间的转换
上节的内容归纳为一句话,即“一个空间中有无数组标准正交基,每一组标准正交基都对应一个坐标系。但是每个空间中有且仅有一组标准基,构成该空间的标准坐标系。”
本节中讨论的是坐标系之间相互转换的最基本的问题,一个坐标系与标准坐标系的转换。
依旧以 ( 12 , 8 ) (12, 8) (12,8)这一点作为例子,
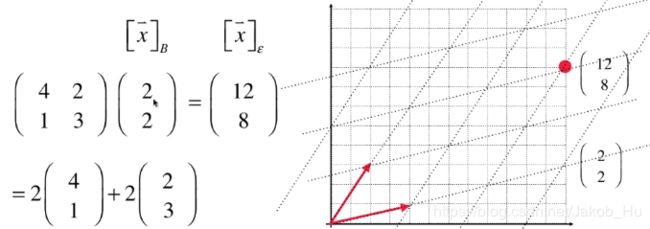
u ⃗ = ( 4 , 1 ) T = 4 e 1 ⃗ + 1 e 2 ⃗ v ⃗ = ( 2 , 3 ) T = 2 e 1 ⃗ + 3 e 2 ⃗ [ x ⃗ ] B = [ ( 2 , 2 ) T ] B = 2 u ⃗ + 2 v ⃗ = 2 ( 4 e 1 ⃗ + 1 e 2 ⃗ ) + 2 ( 2 e 1 ⃗ + 3 e 2 ⃗ ) \vec{u}=(4,1)^T=4\vec{e_1}+1\vec{e_2}\\\vec{v}=(2,3)^T=2\vec{e_1}+3\vec{e_2}\\ [\vec{x}]_B=[(2,2)^T]_B=2\vec{u}+2\vec{v}=2(4\vec{e_1}+1\vec{e_2})+2(2\vec{e_1}+3\vec{e_2}) u=(4,1)T=4e1+1e2v=(2,3)T=2e1+3e2[x]B=[(2,2)T]B=2u+2v=2(4e1+1e2)+2(2e1+3e2)
因为 ( 4 , 1 ) (4, 1) (4,1)和 ( 2 , 3 ) (2, 3) (2,3)这两个基向量是在标准坐标系下衡量的,所以通过上面的转换可以将 ( 2 , 2 ) (2, 2) (2,2)这一点转换到标准坐标系中。将这一规律进行总结,
假设有一组基 B = { b 1 ⃗ , b 2 ⃗ , b 3 ⃗ , . . . b n ⃗ } B=\{\vec{b_1},\vec{b_2},\vec{b_3},...\vec{b_n}\} B={b1,b2,b3,...bn},设立矩阵 P B = ( b 1 ⃗ b 2 ⃗ . . . b n ⃗ ) P_B=\begin{pmatrix}\vec{b_1}&\vec{b_2}&...&\vec{b_n}\end{pmatrix} PB=(b1b2...bn)。在这组基下的一个向量 [ x ⃗ ] B [\vec{x}]_B [x]B,有 [ x ⃗ ] ϵ = P B [ x ⃗ ] B [\vec{x}]_{\epsilon}=P_B[\vec{x}]_B [x]ϵ=PB[x]B。其中 P B P_B PB称为坐标转换矩阵。
相应的,如果一组正交基构成的坐标转换矩阵 P B P_B PB,将标准坐标系中的向量转入到 B B B构成的坐标系也是十分容易的
P B − 1 [ x ⃗ ] ϵ = P B − 1 P B [ x ⃗ ] B P B − 1 [ x ⃗ ] ϵ = [ x ⃗ ] B P_B^{-1}[\vec{x}]_{\epsilon}=P_B^{-1}P_B[\vec{x}]_B\\P_B^{-1}[\vec{x}]_{\epsilon}=[\vec{x}]_B PB−1[x]ϵ=PB−1PB[x]BPB−1[x]ϵ=[x]B
任意坐标系之间的转换
标准单位矩阵作为桥梁
两个任意坐标系之间的转换在任意坐标系与标准坐标系转换的基础上进行是十分简单的,可以直接使用标准坐标系作为桥梁,对两个任意坐标系进行连通。

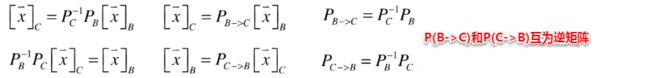
结论验证
具体的转换过程可以推导如下,
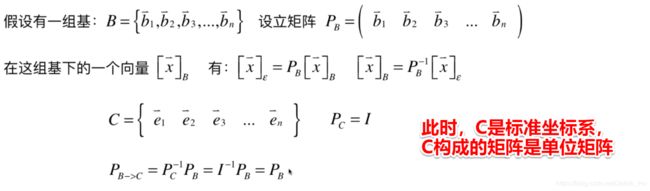
同理,反过来将标准单位矩阵转换为坐标系 B B B也依旧是成立的,
P C → B = P B − 1 P C = P B − 1 I = P B − 1 P_{C\rightarrow B}=P_B^{-1}P_C=P_B^{-1}I=P_B^{-1} PC→B=PB−1PC=PB−1I=PB−1
不使用单位坐标系为桥梁的情况
在前面的讲解中,基向量实际上是这些向量在标准坐标系中的表示,

所以可以进行如下推导,如果已知一组基向量在另一组基向量对应的坐标系中的表示,此时可以不使用单位向量作为转换的桥梁。

此时可以很容易求取出B坐标系的向量在C坐标系中的表示,即
[ x ⃗ ] C = P B → C [ x ⃗ ] B [\vec{x}]_C=P_{B\rightarrow C}[\vec{x}]_B [x]C=PB→C[x]B
简单地使用下面的一个例子进行证明,
