【VIO笔记（学习VINS的必备基础）】第六讲 视觉前端

系列教程来自某学院，侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力，不然直接撸网上的各种VINS解析完全云里雾里-_-!

前端工作的综述

通常的 SLAM 框架由前后端共同构成，前端:提取特征点,追踪相机 Pose,定位相机；后端:提供全局优化或滑动窗口优化。
前端对于SLAM的最终追踪效果的贡献比较大，而后端虽然有很多种做法，例如基于滤波、滑动窗口等等，但是只要后端的实现是对的，对于最后的效果影响却不大。
对于一个好的前端，我们希望它：
• 追踪效果好,不容易丢
• 计算速度快
• 累计误差小
下面这张图给出了各种主流VO之间的一个对比：

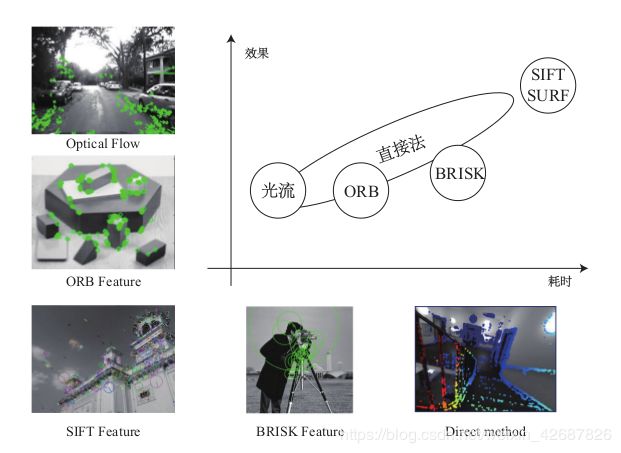
可以看到耗时和效果整体上是成正比的，所以当计算量足够时当然使用SIFT这样的方法，然而在实时的场景中，目前SIFT提取一次特征点需要200ms左右，无法使用。而ORB在10-15ms，然而效果较差，直接法则是一个跨度较大的方法，课上高博说直接法在实际运用时比特征点法是要效果更好的，特征点法经常会面临特征缺失的情况，例如上图中很多有天空的场景，特征点是很少的，两边的物体也很难做匹配，比如杂草等。
下面列出了一些结论：

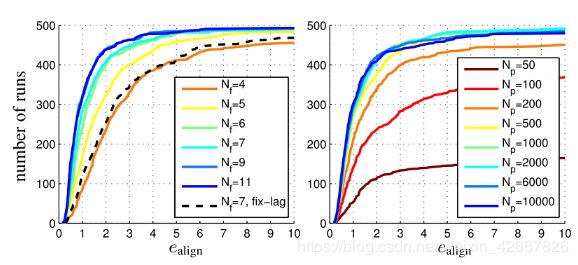
这是光流和特征点法的结论，在角点比较好的情况下，使用FAST+光流/GFTT+光流是比较实用的方法，而直接法则不太依赖于角点，但实现效果根据选点数量变化较大，下图是DSO论文中的内容，曲线越靠左上侧越好。在点数达到500以上的时候，效果的提示就不太明显了，可以看到黄色的线下方的其他线每加一个点数，就会有很大的提升。

特征点提取、匹配和光流

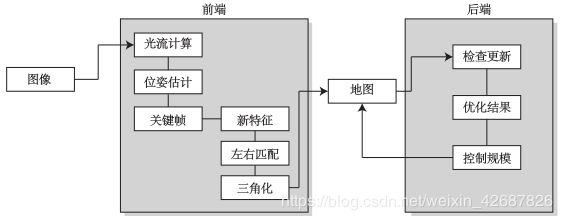
接下来介绍了一个光流方案的前端，下图是一个传统的双目光流的系统框图，单目的系统把左右匹配那一块修改成前后匹配就行了，其他部分也相同。

为什么需要角点

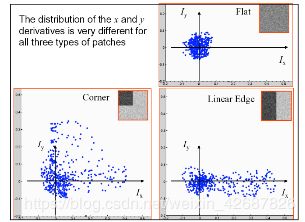
之前也提到光流法对角点比较依赖，这是为什么呢？下面这个例子做了很好的说明：
当我们选取了角点时，很容易辨认出下一张图中第二个绿色框是和上一帧匹配的，而当我们没有选取角点而是选取了一块空白的区域，就很难进行判断。那么这里提一下，如果没有提到角点，而是提到了一个边，例如左边是白色右边是黑色的部位怎么办？这时是可以使用直接法来进行位姿估计的，直接法是先利用一部分点计算出大概的变换矩阵，之后再通过对应的特征点来进行调整。

角点的提取

那么如果要使用光流，那就要确定提取到的是不是角点，下面介绍几种方法：

1. Harris角点
   
   利用角点附近块的两个特征值大小,可以判断该区是否为角点。
   

2. FAST/GFTT 角点
   GFTT是在 Harris 基础改进:Shi-tomasi 分数,增加固定选点数,等等
   FAST则是只要点周围的连续N个点的灰度低于该点则认为它是角点，选取9点的就叫FAST-9。
   FAST的速度最快，在1ms以内。GFTT则在10ms左右。

光流的计算

光流可以追踪一个时刻的角点在下个时刻的图像位置。
基于灰度不变假设：

对上式进行一阶泰勒展开：

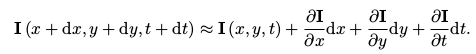
由于两项相等可以消去，最后得到：

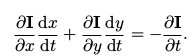
我们所求的就是$\frac{dx}{dt}$和$\frac{dy}{dt}$，那么这就是一个二元一次方程，无法通过一个式子求解，所以我们再假设在一个窗口内所有像素的运动是一样的，这样就获得一个超定的方程组，对其使用最小二乘求解即可求得u和v。
针对一些场景下灰度不变假设并不成立，这里介绍一种带warp的光流：

如下图这个车不断的在变化，那么我们在直接加的基础上使用一个仿射变换：


其中 p 1 − p 6 为 W 的参数,需要在线估计。
同时还可以给光流加上一个金字塔：

在图片中物体运动较快时，两帧之间的位移就会很大，这样就会使得前面的假设不满足，从而出现误差，这样我们就希望它能够运动的慢一点，通过缩小像素的尺寸就可以做到这一点，具体的原理可以参考：总结：光流–LK光流–基于金字塔分层的LK光流–中值流

光流的总结

在SLAM中，光流可以追踪上一帧的角点，并一直追踪该角点,直到超出图像范围或被遮挡，在单目 SLAM 中,新提出的角点没有 3D 信息,因此可通过追踪角点在各图像位置,进行三角化。
然而光流在SLAM中也存在局限性：
1 容易受光照变化影响
2 只适合连续图像中的短距离追踪,不适合更长距离
3 图像外观发生明显变化时不适用(例:远处的角点凑近看之后不为角点了)
4 对角点强依赖,对 Edge 类型点表现较差
5 稀疏光流不约束各点光流的方向统一,可能出现一些 outlier。

关键帧与三角化

在第五讲中已经有提到，我们的滑动窗口不能每一帧图像都进行一样的更新和边缘化的操作，这样的话如果相机处在静止状态，会导致滑动窗口中的图像在一段时间后全是相同的图像，导致估计效果变差。按照上一讲VINS的策略，我们在到来的时候第二新的帧是关键帧时marg掉最老的一帧，否则丢弃视觉信息只进行IMU的更新，这样在静止的时候也能够保持良好的性能。

关键帧

那么如何挑选出关键帧呢？

1. 关键帧之间不必太近(退化或三角化问题)
   太近导致的问题和静止其实类似，会导致整个图的顶点离得过近。
2. 关键帧之间不能太远(共视点太少)
   太远会导致共视点太少，使得在零空间中会发生新的移动，因为没有共视点就无法进行两者间位姿的估计。
3. VIO 中,定期选择关键帧(假设 $b_g$ ,$b_a$ 在关键帧期间不变)
   结论：对于非关键帧,只执行前端算法,不参与后端优化，因此,对于非关键帧,它的误差会逐渐累积。直到该帧被作为关键帧插入后端,BA 才会保证窗口内的一致性，所以在计算量允许范围内,且不引起退化时,应尽可能多地插入关键帧。

三角化

在单目SLAM中，通常在插入关键帧时计算新路标点的三角化，下面先介绍三角化的原理：
考虑某路标点 y 在若干个关键帧 k = 1, · · · , n 中看到。则有：

其中${\lambda }_k$是路标点的深度，$x_k={\left[\begin{array}{ccc}{u}_k& v_k& 1\end{array}\right]}^T$，Pk是投影矩阵，y则是我们要求的路标点坐标，用齐次坐标表示。这个式子的第三行可表示为：

将它带入前两行：

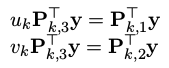
每次观测都会获得这样的一组方程，当有多次相机观测到这个路标点时，可以得到：

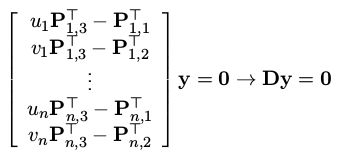
之后使用最小二乘的方法即可获得y的估计值：

这里先给出结论：$Dy=0$的最优解y等于${\mathbf{D}}^T\mathbf{D}$的最小奇异值对应的奇异值向量，也就是$y=u_4$
这里要用到SVD分解：奇异值分解(SVD)原理与在降维中的应用，${\mathbf{D}}^T\mathbf{D}$的奇异值分解为：

也就是我们的特征值分解$A=W\Sigma W^{-1}$将特征值矩阵$\Sigma$展开成连加的形式，将这个式子带入最小二乘，可以写成：

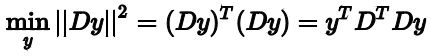
y可以由${\mathbf{D}}^T\mathbf{D}$的奇异值向量线性组合得到,也就是可以表示成如下形式：

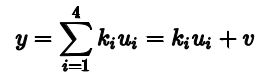
其中


由于u和v正交，所以后两项为0， 且Du=奇异值乘对应的u，带入得到：

当v取0时上式有最小值，也就是仅由奇异值去确定，而奇异值随着i越大越小，所以在这里取4。

k4为1，所以y最小就是u4。
下面用程序来实现三角化。

三角化程序实现

这里只将重要代码贴上来：

/// TODO::homework; 请完成三角化估计深度的代码
    // 遍历所有的观测数据，并三角化
    Eigen::MatrixXd P_est;           // 结果保存到这个变量
    P_est.setZero();
    /* your code begin */
	auto loop_times = camera_pose.size()-start_frame_id;
	Eigen::MatrixXd D((loop_times)*2,4);
    for(int j=0;j<loop_times;++j)
	{
		Eigen::MatrixXd T_tmp(3,4);
        T_tmp.block<3,3>(0,0)=camera_pose[j+3].Rwc.transpose();
        T_tmp.block<3,1>(0,3)=-camera_pose[j+3].Rwc.transpose()*camera_pose[j+3].twc;
        auto P_r1 = T_tmp.block<1,4>(0,0);
	    auto P_r2 = T_tmp.block<1,4>(1,0);
        auto P_r3 = T_tmp.block<1,4>(2,0);
    
        D.block<1,4>(2*j,0)=camera_pose[j+3].uv[0] * P_r3-P_r1;
        D.block<1,4>(2*j+1,0)=camera_pose[j+3].uv[1] * P_r3-P_r2;
    }
    Eigen::Matrix4d D_res=D.transpose()*D;
    Eigen::JacobiSVD<Eigen::Matrix4d> svd(D_res,Eigen::ComputeFullU|Eigen::ComputeFullV);
    auto res_U = svd.matrixU();
    auto res_V = svd.matrixV();
    std::cout << "U=" << res_U << std::endl;
    auto tmp = res_U.rightCols(1);
    P_est=(tmp / tmp(3)).transpose().leftCols(3);
    /* your code end */
    
    std::cout <<"ground truth: \n"<< Pw.transpose() <<std::endl;
    std::cout <<"your result: \n"<< P_est <<std::endl;
    return 0;

首先将所有观测到该路标点的pose都遍历一遍，构建D矩阵。之后对${\mathbf{D}}^T\mathbf{D}$进行SVD分解，然后直接去取分解得到的U矩阵的第四列，注意这里要进行归一化，之后得到估计的y值。运行结果如下，发现和真实值相同了，说明程序效果很好。

最后的矩阵提取要用到一些Eigen的操作，这有一篇总结的文章不错可以参考：Eigen子矩阵操作