【算法】如何根据算法在赌场发家致富?汤普森采样之多臂强盗算法!
汤普森采样—Thompson Sampling 之概念篇
关键词:机器学习,在线学习,人工智能,强化学习
如果你已经熟悉了概念可以直接看代码篇:
【算法应用】Thompson Sampling–汤普森采样应用之代码篇 (Python)
1.简介
汤普森采样是最早由William R. Thompson在1933年提出。最初Thompson在研究两种药物,他想要在尽量少的给病人次优的情况下研究出来哪一种最好。试着试着他就整出来一个客观的选样法,也就是汤普森采样的雏形。而在这之后又不断地有科学家研究该采样方法,并且延伸到很多实用问题上。
2.概念
2.1模型概念
这里用一个流程表示Thompson Sampling 的原理:
a.为每一个可能的选项建立一个贝塔分布(Beta Distribution),在有先验性经验的情况下可调整其中参数α与β的初始值,这里我们举例α与β的初始值都为1(Uniform Distribution)。
b.使每个贝塔分布产生一个随机数值。
c.选择所得结果中最大值为本次选项。
d.根据实验结果调整参数,即α与β。
e.重复整个过程
这里我们第一轮的beta值中,A是最大的,那么我们选择A为本次的选项并获得了回报值1,更新A的模型即增加α的值为2。那么在第2轮中,A的贝塔值就更容易产出一个较大的数。反之我们会增加β的值,A的贝塔值就会比较容易产出一个较小的数。
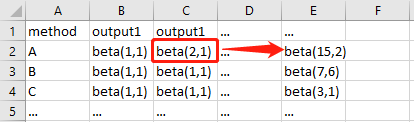

简单吧? 上图!
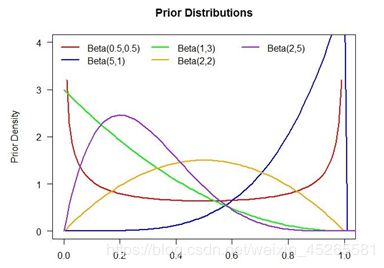
简单来说α小于β时,图像就被往左push,给出的结果也就偏小。
α大于β时,图像就被往右push,给出的结果也就偏大。
f ( α , β ; x ) = Γ ( α + β ) Γ ( α ) Γ ( β ) x α − 1 ( 1 − x ) β − 1 f(\alpha ,\beta ;x)=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )} x^{\alpha -1}(1-x)^{\beta -1} f(α,β;x)=Γ(α)Γ(β)Γ(α+β)xα−1(1−x)β−1
贝塔分布-Beta Distribution 不会也没什么关系
2.2什么是多臂强盗问题?
#本文中所举例子皆是为了学术意义,请大家珍爱生命远离赌博!
我们的主角Tom是一个赌吧老哥,生平最爱玩老虎机。他认为赌场中老虎机的奖励的模式是有特定分布的,那么他新来到一家赌场后他只要找到那个奖励最多的老虎机,他就可以发家致富走向人生巅峰了不是吗。

这里假设他知道这些老虎机大概的情况,但不知道每一个老虎机的平均奖励有多高。
说到这里小伙伴就明白了,我们要解决的就是:
1)最大程度减少Tom在寻找这一台lucky老虎机过程中的损耗(在一些奖励少的老虎机上的cost);
2)追求global maximum防止Tom一直死磕local maximum,也就是当Tom试到第n台老虎机时,他发现这一台老虎机比之前的都高很多,如果基于贪心算法(Greedy algorithms)他会把所有钱画在这个local maximum上,但其实第n+1台所给的平均奖励要更高。那这样就会造成损失。 是不是很简单?

2.3定义变量
好,Tom老哥决定搏一搏,看看单车能不能变摩托。于是Tom老哥踩点了赌场的情况:
赌场中老虎机数量:N
老虎机奖励遵从伯努利(Bernoulli):胜利获奖,失败没有奖励
老虎机奖励(Reward):r=1
每个老虎机累计胜利(Success):Si --> r=1 (i=1,2,3,…,N)
每个老虎机累计失败(Fail):Fi --> r=0 (i=1,2,3,…,N)
Tom口袋里的钱可以玩的次数:T
2.4基础汤普森采样模型
i.为每一个老虎机i(i=1,…,N)建立贝塔分布,且初始参数为(1,1)。
*下面的部分循环T次(t=1,2,3,…,T):
ii.通过每个老虎机i的贝塔分布
B e t a ( S i + 1 , F i + 1 ) Beta(S_{i}+1,F_{i}+1) Beta(Si+1,Fi+1)
获得每个老虎机的贝塔值。
iii.选取有最大贝塔值的那一台最为本次的选择 i(t), 并获得 i(t) 的结果。
iv.根据回报 r(t) 的值更新 i(t)的参数:
{ S i = S i + 1 如果胜利 → r = 1 F i = F i + 1 如果失败 → r = 1 \left\{\begin{matrix} S_{i}=S_{i}+1&\text{如果胜利} \rightarrow r=1\\ F_{i}=F_{i}+1& \text{如果失败} \rightarrow r=1 \end{matrix}\right. {Si=Si+1Fi=Fi+1如果胜利→r=1如果失败→r=1
注意:这里只更新本次选择的i(t)的贝塔分布的参数,所以在下一轮采集贝塔值时,A的模型被更新为:
{ B e t a ( S i + 1 + 1 , F i + 1 ) 如果胜利 → r = 1 B e t a ( S i + 1 , F i + 1 + 1 ) 如果失败 → r = 1 \left\{\begin{matrix} Beta(S_{i}+1+1,F_{i}+1)&\text{如果胜利} \rightarrow r=1\\ Beta(S_{i}+1,F_{i}+1+1)& \text{如果失败} \rightarrow r=1 \end{matrix}\right. {Beta(Si+1+1,Fi+1)Beta(Si+1,Fi+1+1)如果胜利→r=1如果失败→r=1
***结束–>返回 ii
3.结论
最终Tom所建立的模型会探索赌场中的所有老虎机,并在一定的尝试数量后找到属于Tom的那一台lucky老虎机。而我们所要研究的主要问题就是如何减少Tom在这个过程中的损耗。可以使用的方法有:1)修改模型;2)调整收益参数。在本篇中我们所采用的例子只有两个可能,而在现实中会有更多可能的结果,那么通过建立更贴合的收益公式就会很大程度上加快global maximum的寻找。
#本文中所举例子皆是为了学术意义,请大家珍爱生命远离赌博!
Reference:
1. S.Agrawal & N.Goyal ‘AnalysisofThompsonSamplingfortheMulti-armedBanditProblem’
url: http://proceedings.mlr.press/v23/agrawal12/agrawal12.pdf
