【数字逻辑】学习笔记 第五章 时序逻辑电路(概述和集成触发器)
文章目录
- 一、时序逻辑电路概述
- 1. 基本概念和核心部件
- 2. 时序逻辑电路的特点
- 3. 时序逻辑电路的分类
- 二、集成触发器介绍
- 1. 触发器概述
- 2. 触发器的特点
- 3. 触发器的分类
- 4. 触发器逻辑功能的描述方式
- 三、集成触发器
- 1. 基本 `R-S` 触发器
- (1) 电路结构
- (2) 工作原理
- 输入 R D ‾ = 0 , S D ‾ = 1 \overline{R_D} = 0, \overline {S_D}= 1 RD=0,SD=1 时,置 0 0 0
- 输入 R D ‾ = 1 , S D ‾ = 0 \overline{R_D} =1, \overline {S_D}= 0 RD=1,SD=0 时,置 1 1 1
- 输入 R D ‾ = 1 , S D ‾ = 1 \overline{R_D} =1, \overline {S_D}= 1 RD=1,SD=1 时,保持
- 输入 R D ‾ = 0 , S D ‾ = 0 \overline{R_D} =0, \overline {S_D}= 0 RD=0,SD=0 时,保持
- (3) 逻辑功能的描述
- a. 状态转移真值表(功能表)
- b. 特征方程——用逻辑函数描述触发器的功能
- c. 状态转移图——用图形来描述触发器的功能
- d. 激励表 —— 是状态转移图的表格表达方式
- e. 波形图 —— 输出信号波形随输入信号发生变化
- (4) 特点
- 2. 电平触发的触发器
- (1) 钟控 `R-S` 触发器
- a. 电路结构
- b. 工作原理
- c. 功能表
- d. 特征方程
- e. 时序波形图
- (2) 钟控D触发器
- a. 电路结构
- b. 工作原理
- c. 特征方程
- d. 状态转移真值表
- e. 波形图
- (3) 钟控J-K触发器
- a. 电路结构
- b. 工作原理
- c. 特征方程
- d. 功能表
- e. 波形图
- (4) 钟控T触发器
- a. 电路结构与工作原理
- b. 特征方程
- c. 功能表
- (5) 电平触发方式的动作特点
- 3. 边沿触发的触发器
- (1) 边沿D触发器
- a. 基本结构
- b. 状态方程
- c. 功能表
- d. 波形图
- 四、触发器汇总
- 1. 基本R-S触发器
- 2. 钟控R-S触发器
- 3. J-K触发器
- 4. D触发器
- 5. T触发器
- 五、练习题
一、时序逻辑电路概述
1. 基本概念和核心部件
- 基本概念:具有记忆功能的电路
- 触发器 : 能记忆 1 1 1 位二进制数的电路
本章我们重点关注:
- 时序逻辑电路的分析与设计的方法
- 实际应用:计数器与寄存器
2. 时序逻辑电路的特点
数字逻辑电路分为:组合逻辑电路和时序逻辑电路
- 组合逻辑电路的特点:输出随当前输入变化
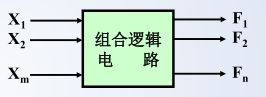
- 时序逻辑电路的特点:
功能:任何时刻的稳定输出,不仅与 该时刻 的输入有关,还与电路 原状态 有关,即与以前的输入有关
结构: 由 组合电路 和 存储电路 组成
3. 时序逻辑电路的分类
按有无统一时钟脉冲分:
- 同步: 有统一的时钟
CP,状态变更与CP同步 - 异步: 无统一
CP,状态变更不同步,逐级进行
按输出信号特点分:
- 米里型(Mealy): 输出信号不仅与存储状态有关,还与外部输入有关
- 莫尔型(Moore): 输出信号仅与存储状态有关(外部输入改变存储状态,从而改变输出)
二、集成触发器介绍
1. 触发器概述
数字电路对二进制信号的处理无非是数值运算和逻辑运算,加上存储。数值逻辑运算电路的设计属于组合电路,而存储则属于时序电路。
能够存储 1 1 1 位二值信号的基本单元电路统称为触发器(Flip-Flop),简称 FF ,又称为双稳态触发器。
触发器是构成时序逻辑电路的基本单元电路。
2. 触发器的特点
- 有两个稳定状态(简称稳态),用来表示逻辑 0 0 0 和 1 1 1,一个触发器可存储 1 1 1 位二进制数码
- 在输入信号作用下,触发器的两个稳定状态可相互转换(称为状态的翻转)
- 输入信号作用后,新状态可长期保持下来,电路具有记忆功能
触发器的现态和次态
- 现态 (现在状态):输入变化前,触发器所处的状态
- 次态 (下一状态):输入变化后,触发器进入的状态(次态是对某一时刻而言,过了该时刻就应看作现态)
3. 触发器的分类
- 按逻辑功能分:
R-S触发器、D型触发器、J-K触发器、T型触发器等; - 按触发方式分: 电平触发方式、脉冲触发方式和边沿触发方式
4. 触发器逻辑功能的描述方式
状态转移真值表(功能表)、特征方程、激励表、状态转换图、波形图(时序图)等
三、集成触发器
1. 基本 R-S 触发器
基本R-S触发器,又叫SR锁存器,是构成各种触发器的基本部件,也是最简单的一种触发器。
锁存器——不需要触发信号,由输入信号直接完成置 0 0 0 或置 1 1 1 操作。
触发器——需要一个触发信号 ,称为时钟信号CLOCK,只有触发信号有效时,才按输入信号完成置 0 0 0 或置 1 1 1 操作。
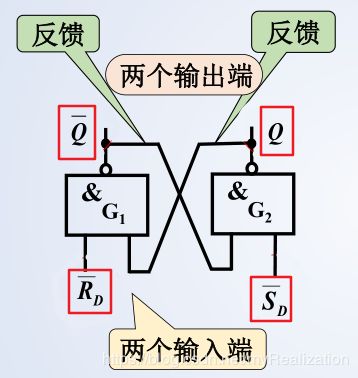
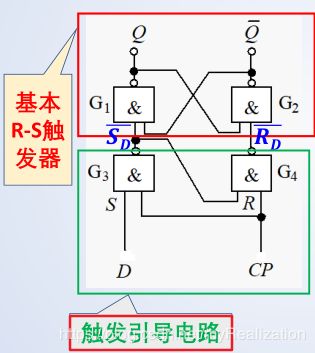
(1) 电路结构
反馈:正是由于引入反馈,才使电路具有记忆功能!
R-S触发器的状态:(输出 Q Q Q 和 Q ‾ \overline Q Q 互为相反逻辑,方便工作原理的分析)
- 0 0 0 态: Q = 0 , Q ‾ = 1 Q=0,\overline Q=1 Q=0,Q=1
- 1 1 1 态: Q = 1 , Q ‾ = 0 Q=1, \overline Q=0 Q=1,Q=0
| R D ‾ \overline {R_D} RD | S D ‾ \overline {S_D} SD |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 1 | 0 |
| 0 | 1 |
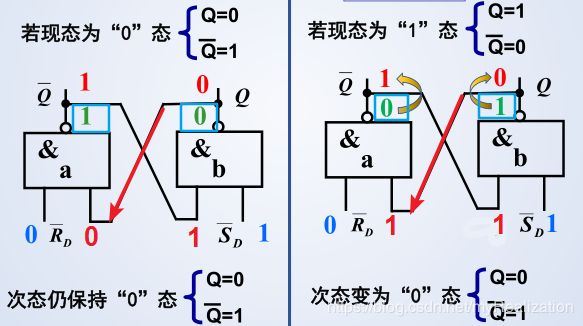
(2) 工作原理
输入 R D ‾ = 0 , S D ‾ = 1 \overline{R_D} = 0, \overline {S_D}= 1 RD=0,SD=1 时,置 0 0 0
输入 R D ‾ = 1 , S D ‾ = 0 \overline{R_D} =1, \overline {S_D}= 0 RD=1,SD=0 时,置 1 1 1

输入 R D ‾ = 1 , S D ‾ = 1 \overline{R_D} =1, \overline {S_D}= 1 RD=1,SD=1 时,保持

输入 R D ‾ = 0 , S D ‾ = 0 \overline{R_D} =0, \overline {S_D}= 0 RD=0,SD=0 时,保持
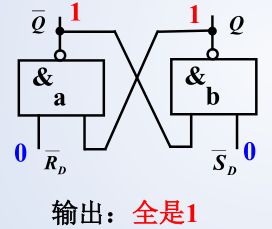
注意:当两个输入端由 0 0 0 变为 1 1 1 时,翻转快的门输出变为 0 0 0 ,另一个不得翻转。因此,该状态为不定状态。
(3) 逻辑功能的描述
a. 状态转移真值表(功能表)
基本R-S触发器的状态转移真值表——反映触发器状态变化与输入之间的关系

基本R-S触发器的简化功能表

b. 特征方程——用逻辑函数描述触发器的功能
基本R-S触发器状态转移表
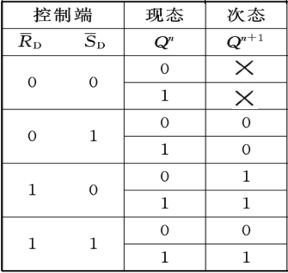
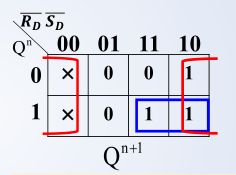
{ Q n + 1 = S D + R D ‾ Q n S D ‾ + R D ‾ = 1 \left\{ \begin{aligned} Q^{n+1} &= S_D + \overline {R_D}Q^n\\ \overline {S_D} +\overline {R_D} &= 1 \end{aligned} \right. {Qn+1SD+RD=SD+RDQn=1
约束条件: S D ‾ , R D ‾ \overline {S_D},\overline {R_D} SD,RD 不能同时为零。
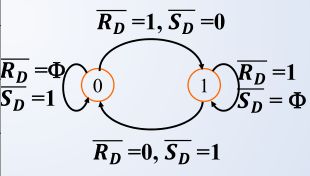
c. 状态转移图——用图形来描述触发器的功能
d. 激励表 —— 是状态转移图的表格表达方式
基本R-S触发器的激励表:
激励表描述触发器由现态 Q n Q^n Qn 转移到次态 Q n + 1 Q^{n+1} Qn+1 时对输入控制信号的要求:

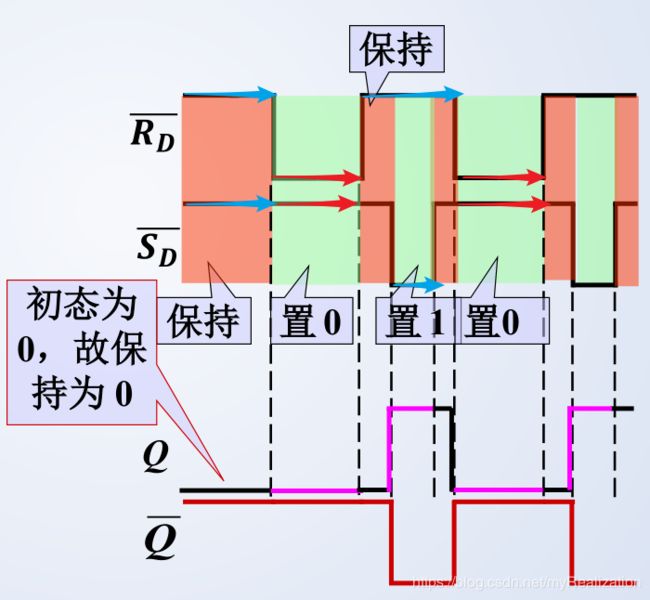
e. 波形图 —— 输出信号波形随输入信号发生变化
(4) 特点
由于基本R-S触发器的状态由输入信号直接控制,以及存在约束条件,其在应用方面存在很大的局限性和不便。
直接控制:输入信号直接加在输出门上,在输入信号全部作用时间内,都能直接改变输出端的状态,即只要有输入信号,就能作用于电路。
2. 电平触发的触发器
在数字系统中, 为协调各部分的动作, 常常要求某些触发器在 同一时刻 动作(即改变状态,也称为翻转)。 这就要求有一个同步信号来控制,这个控制信号叫做 时钟脉冲信号(Clock Pulse,CP),Clock Pulse 是一串周期性的矩形脉冲。
具有时钟脉冲控制的触发器统称为 时钟触发器 ,又称 钟控触发器 。电平触发器(也称同步触发器)是其中最简单的一种。
(1) 钟控 R-S 触发器
a. 电路结构
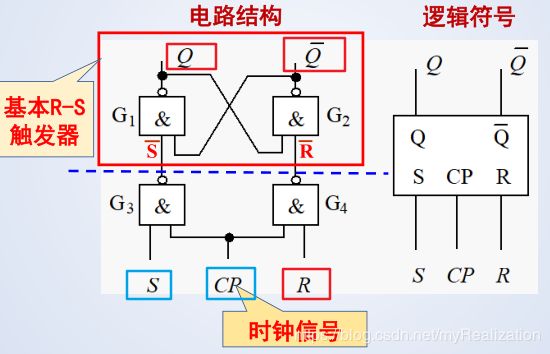
b. 工作原理
C P = 0 CP=0 CP=0 时,触发器保持原态,G3 门和 G4 门的输出被锁定为 1 1 1 , 基本R-S触发器状态保持不变,触发器保持原态。

C P = 1 CP=1 CP=1 时,基本R-S触发器状态由 R R R 和 S S S 决定。
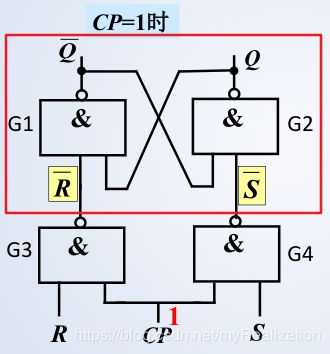
c. 功能表
钟控 R-S 触发器的功能表:
| CP | R | S | Q Q ‾ Q \quad \overline Q QQ |
|---|---|---|---|
| 0 0 0 | Φ \Phi Φ | Φ \Phi Φ | 保持 |
| 1 1 1 | 0 0 0 | 0 0 0 | 保持 |
| 1 1 1 | 0 0 0 | 1 1 1 | 1 0 1 \quad 0 10 |
| 1 1 1 | 1 1 1 | 0 0 0 | 0 1 0 \quad 1 01 |
| 1 1 1 | 1 1 1 | 1 1 1 | 不确定 |

d. 特征方程
- C P = 0 CP=0 CP=0,保持原状态: Q n + 1 = Q n Q^{n+1} = Q^n Qn+1=Qn;
- C P = 1 CP=1 CP=1,基本
R-S触发器:
{ Q n + 1 = S + R ‾ Q n R S = 0 \left\{ \begin{aligned} Q^{n+1} &= S + \overline R Q^n \\ RS &= 0 \end{aligned} \right. {Qn+1RS=S+RQn=0
将时钟信号引入特征方程,可得到: Q n + 1 = ( S + R ‾ Q n ) ⋅ C P + Q n ⋅ C P ‾ Q^{n+1} = (S +\overline RQ^n ) \cdot CP + Q^n \cdot \overline {CP} Qn+1=(S+RQn)⋅CP+Qn⋅CP
e. 时序波形图
初态 Q = 0 Q=0 Q=0 ,在 CP 作用下 Q Q Q 端的波形:(钟控R-S触发器输入信号受约束)
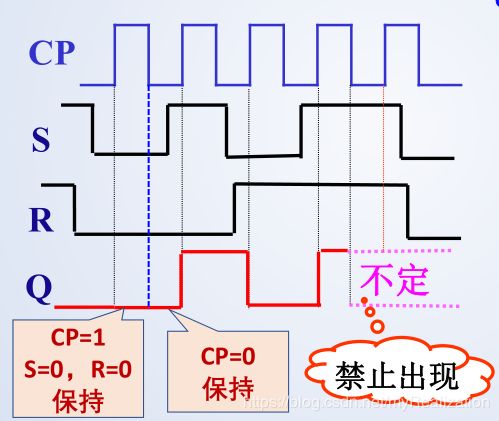
C P = 0 CP=0 CP=0 时,保持原状态;
C P = 1 CP=1 CP=1 时,真值表如下:

(2) 钟控D触发器
a. 电路结构
钟控 D D D 触发器只有一个输入端 D D D , 保证了后端的基本 R-S 触发器的两个输入端 R D ‾ \overline{R_D} RD和 S D ‾ \overline {S_D} SD始终为相反状态。从而解决了电路的输入约束问题。
b. 工作原理
C P = 0 CP=0 CP=0 时,保持原状态:
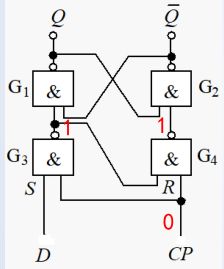

C P = 1 CP=1 CP=1,实现D触发器功能:
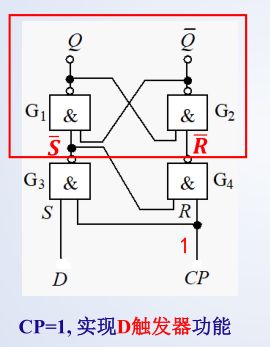
c. 特征方程
C P = 0 CP=0 CP=0 时, Q n + 1 = Q n Q^{n+1} = Q^n Qn+1=Qn;
C P = 1 CP=1 CP=1 时:
{ Q n + 1 = S D + R D ‾ Q n S D ‾ + R D ‾ = 1 S D ‾ = S ‾ = D ‾ R D ‾ = R ‾ = D ‾ ‾ = D \left\{ \begin{aligned} Q^{n+1} = S_D + \overline {R_D} Q^n\\ \overline {S_D}+\overline {R_D} = 1\\ \overline {S_D} = \overline S = \overline D\\ \overline {R_D} = \overline R = \overline {\overline D} = D\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧Qn+1=SD+RDQnSD+RD=1SD=S=DRD=R=D=D
将时钟信号引入特征方程:
Q n + 1 = D ⋅ C P + Q n ⋅ C P ‾ Q^{n+1} = D\cdot CP + Q^n \cdot \overline {CP} Qn+1=D⋅CP+Qn⋅CP
d. 状态转移真值表

其特点如下:
- D触发器的输入信号没有约束限制条件(通过将 D D D 反相输入为 R R R,使得 R ‾ + S ‾ = 1 \overline R + \overline S = 1 R+S=1 始终成立);
- 可实现保持、置 0 0 0 和置 1 1 1 等功能。
e. 波形图
触发器初始状态为 0 0 0:
(3) 钟控J-K触发器
a. 电路结构
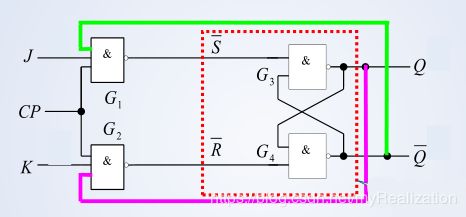
b. 工作原理
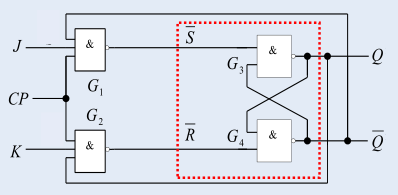
当 C P = 0 CP=0 CP=0 时, S ‾ = 1 , R ‾ = 1 \overline S=1, \overline R = 1 S=1,R=1,触发器处于保持状态 Q n + 1 = Q n Q^{n+1} = Q^n Qn+1=Qn;
当 C P = 1 CP=1 CP=1 时, S ‾ = J Q n ‾ ‾ , R ‾ = K Q n ‾ \overline S = \overline {J \overline {Q^n}}, \overline R = \overline {KQ^n} S=JQn,R=KQn,可得 Q n + 1 = S + R ‾ Q n = J Q n ‾ + K Q n ‾ ⋅ Q n = J Q n ‾ + K ‾ Q n Q^{n+1}= S + \overline RQ^n ={J \overline {Q^n}} + \overline {KQ^n}\cdot Q^n = J\overline {Q^n} + \overline KQ^n Qn+1=S+RQn=JQn+KQn⋅Qn=JQn+KQn
c. 特征方程
将时钟信号引入特征方程:
Q n + 1 = ( J Q n ‾ + K ‾ Q n ) ⋅ C P + Q n ⋅ C P ‾ Q^{n+1} = (J\overline {Q^n} + \overline KQ^n) \cdot CP + Q^n \cdot \overline {CP} Qn+1=(JQn+KQn)⋅CP+Qn⋅CP
由基本R-S触发器的约束条件:
R D ‾ + S D ‾ = 1 \overline {R_D} + \overline {S_D} = 1 RD+SD=1
得到钟控J-K触发器的约束条件:
R D ‾ + S D ‾ = J Q n ‾ ‾ + K Q n ‾ = 1 \overline {R_D} + \overline {S_D} = \overline {J \overline {Q^n}} + \overline {KQ^n}=1 RD+SD=JQn+KQn=1
d. 功能表

无论是从特征方程,还是功能表,都可以看出,钟控J-K触发器不受约束条件限制,因为它把 Q n Q^n Qn 和 Q n ‾ \overline {Q^n} Qn 交错反馈到了输入中。该触发器可以在J、K信号的控制下实现保持、置1、置0和翻转的功能。
e. 波形图
C P = 0 CP = 0 CP=0 时,触发器状态不变。
C P = 1 CP = 1 CP=1 时,触发器根据J 、K信号取值按照JK功能工作。
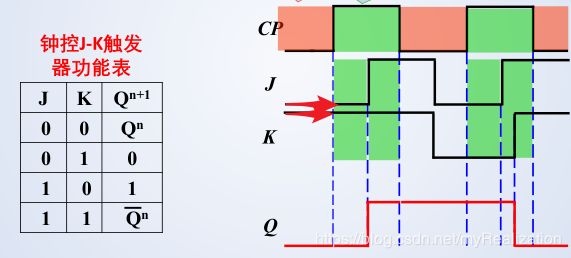
(4) 钟控T触发器
a. 电路结构与工作原理
结合钟控D触发器和J-K触发器的设计原理,就出现了钟控T触发器。

当 C P = 0 CP=0 CP=0 时, S ‾ = 1 , R ‾ = 1 , Q n + 1 = Q n \overline S = 1,\overline R = 1, Q^{n+1} = Q^n S=1,R=1,Qn+1=Qn;
当 C P = 1 CP=1 CP=1 时, S = T Q n ‾ , R = T Q n S = T\overline {Q^n}, R = T {Q^n} S=TQn,R=TQn, Q n + 1 = S + R ‾ Q n = T Q n ‾ + T Q n ‾ ⋅ Q n = T Q n ‾ + T ‾ Q n Q^{n+1} = S + \overline RQ^n = T\overline {Q^n} + \overline {TQ^n}\cdot Q^n = T\overline {Q^n} + \overline TQ^n Qn+1=S+RQn=TQn+TQn⋅Qn=TQn+TQn
b. 特征方程
将时钟信号引入特征方程:
Q n + 1 = ( T Q n ‾ + T ‾ Q n ) ⋅ C P + Q n ⋅ C P ‾ Q^{n+1} = (T\overline {Q^n} + \overline TQ^n)\cdot CP + Q^n \cdot \overline {CP} Qn+1=(TQn+TQn)⋅CP+Qn⋅CP
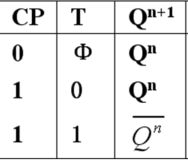
c. 功能表
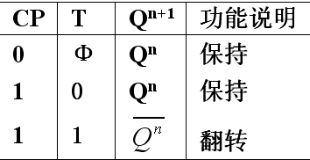
可以看出:
- T触发器的输入信号没有约束限制条件(除了开始介绍的基本R-S触发器和钟控R-S触发器外,其余介绍的都是没有约束条件的);
- 可实现保持和翻转功能。
(5) 电平触发方式的动作特点
- 只有当 C P CP CP 变为有效电平时,触发器才能接受输入信号,并根据输入信号将触发器的输出置成相应的状态;
C P = 1 CP = 1 CP=1 期间翻转的称正电平触发式;
C P = 0 CP = 0 CP=0 期间翻转的称负电平触发式。 - 在 C P CP CP 为有效电平的全部时间里,输入信号的变化都将引起触发器输出状态的变化;
- 在 C P CP CP 有效电平期间,若输入信号多次发生变化,则触发器状态将多次翻转,从而降低了电路的抗干扰能力;
- 在电平触发器在
CP = 有效电平期间,输出发生多次翻转的现象称为空翻。空翻可能会造成误动作!
例:

3. 边沿触发的触发器
边沿触发:
- 只在时钟信号的某一边沿( C P ↑ CP↑ CP↑ 或 C P ↓ CP↓ CP↓ )对输入信号作出响应并引起触发器状态变化(翻转);
- 触发器的次态仅取决于 C P CP CP 的上升沿或下降沿到达时输入的逻辑状态,而与此前、后的状态无关,其它时间的输入也不影响触发器输出,提高了抗干扰能力,可靠性高
边沿触发器只有在 C P CP CP 的上升沿或下降沿瞬间才能接受控制输入信号,改变状态,因此在一个时钟脉冲下,触发器最多只能翻转一次,从根本上杜绝了"空翻"的现象。
(1) 边沿D触发器
a. 基本结构
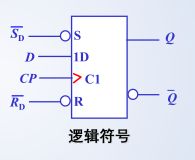
- “>” 表示边沿触发;
CP线顶端没有小圆圈表示"上升沿触发"
异步输入端: S D ‾ , R D ‾ \overline {S_D} , \overline {R_D} SD,RD ,异步输入端对电路的作用与时钟信号无关
- 当 S D ‾ = 1 , R D ‾ = 0 \overline {S_D} =1,\overline {R_D} = 0 SD=1,RD=0 时, Q = 0 , Q ‾ = 1 Q=0, \overline Q = 1 Q=0,Q=1;
- 当 S D ‾ = 0 , R D ‾ = 1 \overline {S_D} =0,\overline {R_D} = 1 SD=0,RD=1 时, Q = 1 , Q ‾ = 0 Q=1, \overline Q = 0 Q=1,Q=0;
- 当 S D ‾ = 1 , R D ‾ = 1 \overline {S_D} =1,\overline {R_D} = 1 SD=1,RD=1 时, 触发器状态变化受输入信号
D和时钟信号CP的控制,触发器的状态仅仅取决于CP信号上升沿到达前瞬间的D信号
b. 状态方程
Q n + 1 = D Q^{n+1} = D Qn+1=D
c. 功能表
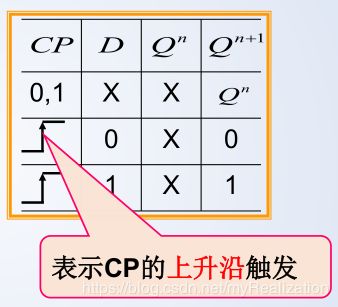
d. 波形图
注意:
- 触发器的翻转发生在 C P CP CP 的上升沿;
- 判断触发器次态的依据是 C P CP CP 上升沿前一瞬间输入端的状态
四、触发器汇总
1. 基本R-S触发器

状态方程:
{ Q n + 1 = S D + R D ‾ Q n S D ‾ + R D ‾ = 1 \left \{ \begin{aligned} &Q^{n+1} = S_D + \overline {R_D} Q^n \\ &\overline {S_D} + \overline {R_D} = 1 \end{aligned} \right. {Qn+1=SD+RDQnSD+RD=1
2. 钟控R-S触发器
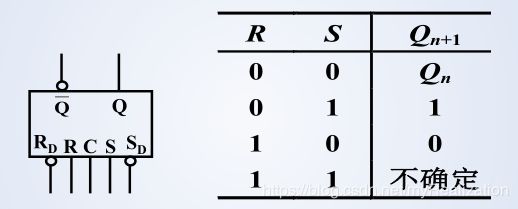
状态方程:
{ Q n + 1 = S D + R D ‾ Q n R S = 0 \left \{ \begin{aligned} &Q^{n+1} = S_D + \overline {R_D} Q^n \\ &RS = 0 \end{aligned} \right. {Qn+1=SD+RDQnRS=0
3. J-K触发器
钟控J-K触发器:(电平触发)
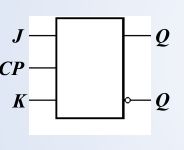

状态方程:
Q n + 1 = J Q n ‾ + K ‾ Q n Q^{n+1} = J\overline {Q^n} + \overline {K} Q^n Qn+1=JQn+KQn
4. D触发器

状态方程:
Q n + 1 = D Q^{n+1} = D Qn+1=D
5. T触发器
钟控T触发器:前面给出了图片;
状态方程:
Q n + 1 = T Q n ‾ + T ‾ Q n Q^{n+1} = T\overline {Q^n} + \overline TQ^n Qn+1=TQn+TQn
这是第五章时序逻辑电路的第一部分,下一部分主要讲的是同步时序和异步时序逻辑电路的分析与设计,更有难度。
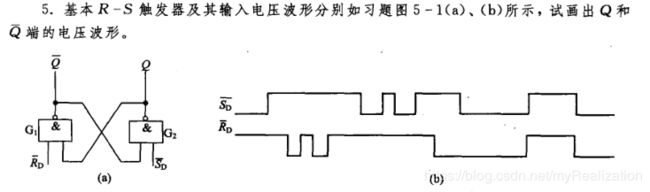
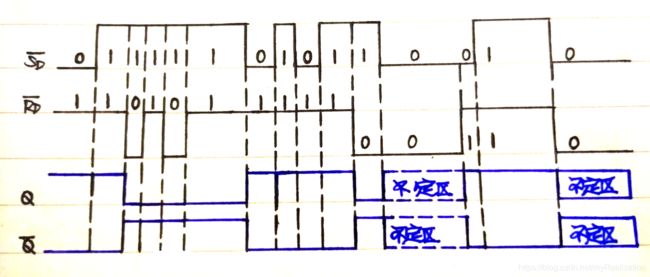
五、练习题