数学建模 —— 自回归模型

一、自回归模型的定义

  将预测对象按照时间顺序排列起来，构成一个所谓的时间序列，从所构成的一组时间序列的变化规律，推断今后变化的可能性及变化趋势、变化规律，就是时间序列预测法。
  时间序列模型其实也是一种回归模型，其基于的原理是，一方面承认事物发展的延续性，运用过去时间序列的数据统计分析就能推测事物的发展趋势；另一方面又充分考虑到偶然因素影响而产生的随机性，为了消除随机波动的影响，利用历史数据，进行统计分析，并对数据进行适合的处理，进行趋势预测。
  自回归模型是用自身做回归变量的过程，即利用前期若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型，它是时间序列中的一个常见形式。

二、自回归模型的表现形式

  考虑一个时间序列的 y₁,y₂,…,y_n，p 阶自回归模型（简称为AR§）表明序列中y_t是前 p 个序列的线性组合及误差项的函数，一般形式的数据模型为：
$$y_t={\Phi }_0+{\Phi }_1{y}_{t-1}+{\Phi }_2{y}_{t-2}+\dots +{\Phi }_p{y}_{t-p}+{\epsilon }_t$$
其中，Φ₀是常数项，Φ₁,…,Φ_p 是模型参数，ε_t是具备均值为 0，方差为 σ 的白噪声（白噪声是指功率谱密度在整个频域内均匀分布的噪声）。

三、Matlab_AR模型阶数确定

  有几种方法来确定。如 Shin 提出基于 SVD的方法，而 AIC和 FPE方法是目前应用最广 泛的方法。 若计算出的 AIC较小，例如小于 -20，则该误差可能对应于损失函数的 10^-10级别， 则这时阶次可以看成是系统合适的阶次。

四、matlab 相关性分析

Pearson相关系数

  考察两个事物（在数据里我们称之为变量）之间的相关程度，简单来说就是衡量两个数据集合是否在一条线上面。其计算公式为：

N表示变量取值的个数。
相关系数r的值介于–1与+1之间，即–1≤r≤+1。其性质如下：

1. 当r>0时，表示两变量正相关，r<0时，两变量为负相关。
2. 当|r|=1时，表示两变量为完全线性相关，即为函数关系。
3. 当r=0时，表示两变量间无线性相关关系。
4. 当0<|r|<1时，表示两变量存在一定程度的线性相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱。

一般可按三级划分：
  |r|<0.4为低度线性相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关。

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

1. 两个变量之间是线性关系，都是连续数据。
2. 两个变量的总体是正态分布，或接近正态的单峰分布。
3. 两个变量的观测值是成对的，每对观测值之间相互独立。

Matlab 实现：

	x=[1;2;3];
	y=[2;5;6];
	r1=corr(x,y,'type','pearson');
	r2=corrcoef(x,y);

结果：

	r1=0.9608
	
	r2=
	
	1.0000 0.9608
	
	0.9608 1.0000

Spearman相关系数

  斯皮尔曼相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的相关系数可以达到+1或-1。

  斯皮尔曼相关系数对数据条件的要求没有皮尔逊相关系数严格，只要两个变量的观测值是成对的，或者是由连续变量观测资料转化得到的，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼相关系数来进行研究。

  使用matlab计算spearman相关系数则比较简单，也是使用corr函数，如下：

	r= corr(x, y, 'type' , 'Spearman');  

注意：使用Matlab自带函数计算斯皮尔曼相关系数时，需要保证X、Y均为列向量；
  求解时间序列的相关系数

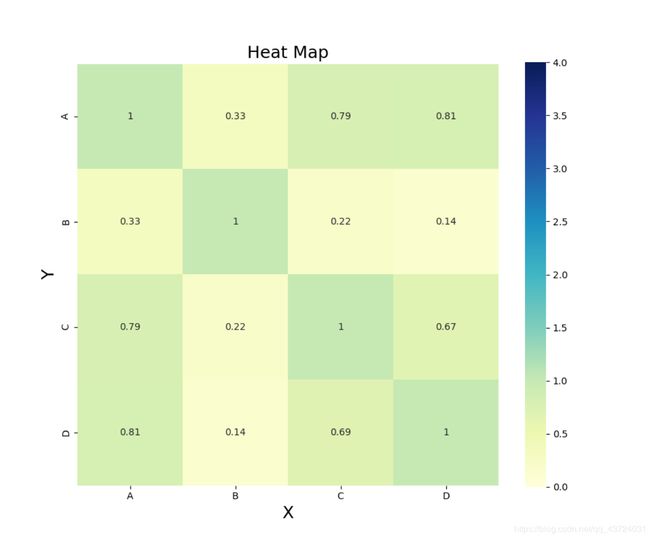
Python 绘制相关系数热力图

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import pearsonr, spearmanr

def dataPlot():
    data1 = [[1,0.3260,0.7916,0.8073],[0.3260,1,0.2162,0.1426],[0.7916,0.2162,1,0.6745],[0.8073,0.1426,0.6945,1]]
    data1 = np.array(data1)
    fig, ax = plt.subplots(figsize=(10, 10))
    key_list = ['A', 'B', 'C', 'D']
    sns.heatmap(pd.DataFrame(np.round(data1, 4), columns=key_list, index=key_list), annot=True, vmax=4, vmin=0,
                xticklabels=True,
                yticklabels=True, square=True, cmap="YlGnBu")
    ax.set_title(' Heat Map ', fontsize=18)
    ax.set_ylabel('Y', fontsize=18)
    ax.set_xlabel('X', fontsize=18)

    plt.savefig('data1.png')
    plt.show()

if __name__ == '__main__':
    dataPlot()

绘制的图像：