线性代数的本质(三)——矩阵和线性变换
线性变换
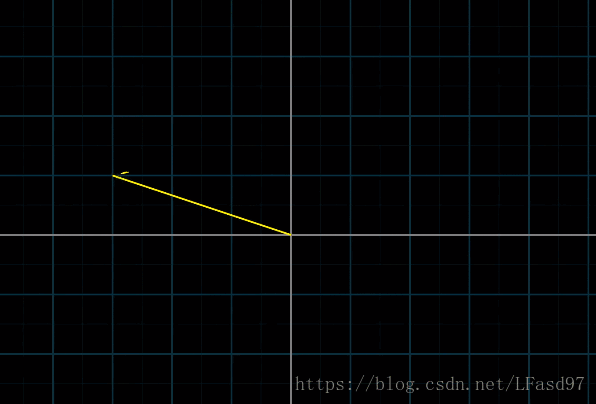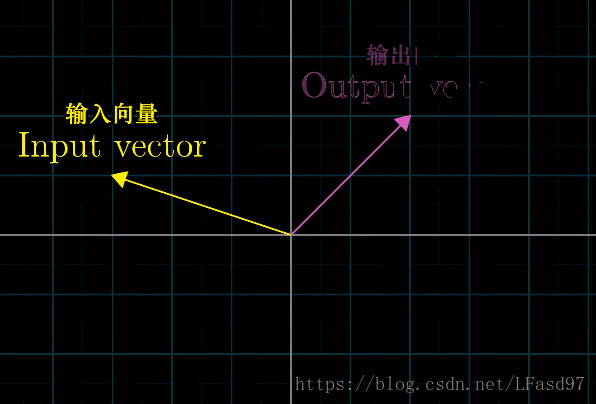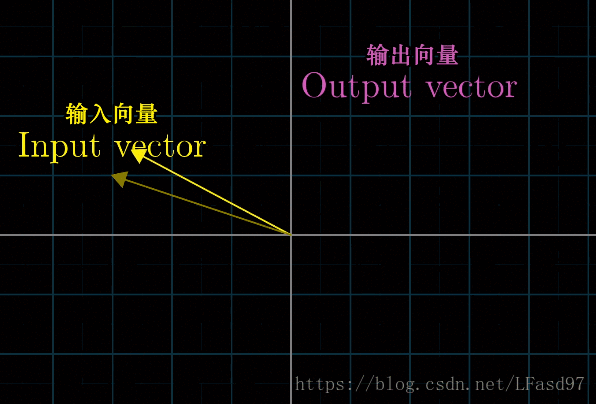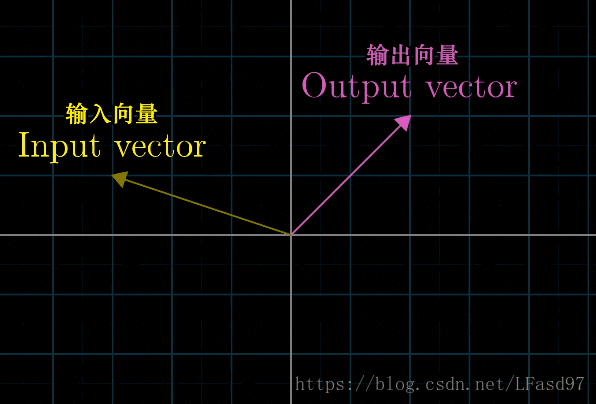
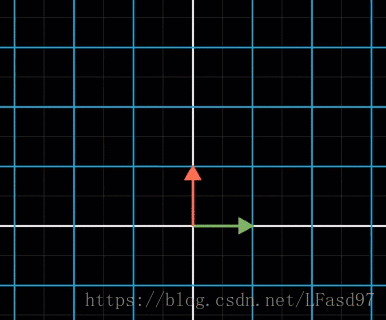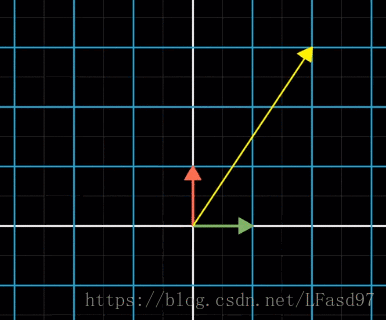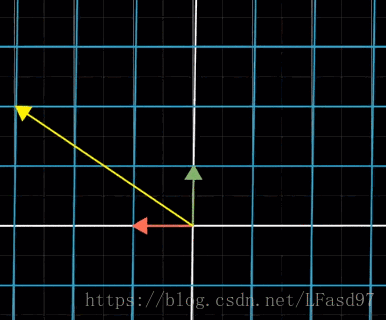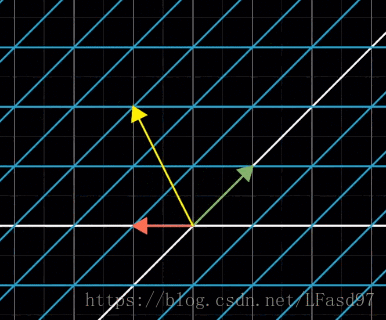
有了前两篇文章的基础,我们现在可以开始理解线性变换和矩阵的意义了。首先,我们可以把变换理解成函数,我们输入一个向量,然后这个变换对应有一个输出向量。这里之所以用“变换”这个词,是因为从向量的理解角度来说,这里像是一种向量的运动,我们看看直观的动图。
我们可以将这种变换理解成对整个空间的变换,这个变换将会对空间中的所有向量生效
线性变换的定义如下
在一个线性空间T中变换A是线性变换是指,对于T中的任意元素 α ⃗ \vec{\alpha} α, β ⃗ \vec{\beta} β,和任意一个标量k,都有
- A ( α ⃗ + β ⃗ ) = A ( α ⃗ ) + A ( β ⃗ ) A(\vec{\alpha} + \vec{\beta}) = A(\vec{\alpha}) + A(\vec{\beta}) A(α+β)=A(α)+A(β)
- A ( k α ⃗ ) = k A ( α ⃗ ) A(k\vec{\alpha}) = kA(\vec{\alpha}) A(kα)=kA(α)
下面两个变换都是线性变换
矩阵
矩阵与线性变换
从上面两个图可以看出,线性变换对空间中所有的向量都产生作用,所以线性变换也会对基向量产生作用。由于所有向量是同时变换,所以变换后的任何向量仍然可以使用原来的坐标并使用变换后的向量进行向量数乘运算获得。
从图中可以看出,在变换后,向量 v ⃗ \vec{v} v 一样可以在变换后的 i ^ \hat{i} i^ 和 j ^ \hat{j} j^ 中使用它的坐标来表示。所以我们可以直接记录变换后的基向量 i ^ \hat{i} i^ 和 j ^ \hat{j} j^ 来表示一个线性变换
所以我们可以将变换后的 i ^ \hat{i} i^ 和变换后的 j ^ \hat{j} j^ 放到一起形成一个矩阵阵。比如上面例子中 i ^ \hat{i} i^ 变成了 [ 1 − 2 ] \begin{bmatrix} 1 \\ -2 \end{bmatrix} [1−2], j ^ \hat{j} j^ 变成了 [ 3 0 ] \begin{bmatrix} 3\\ 0\end{bmatrix} [30],那这个变换我们可以使用矩阵 [ 1 3 − 2 0 ] \begin{bmatrix} 1 & 3 \\-2 & 0 \end{bmatrix} [1−230]来表示。
现在我们想要对一个向量进行一个变换,那我们可以使用代表变换后的基向量矩阵跟这个向量进行矩阵乘法运算。下面来看看完整的例子。
如果我们想要把一个向量逆时针旋转90°,那只需要将基向量 i ^ \hat{i} i^ 和 j ^ \hat{j} j^逆时针旋转90°,我们可以得到这样一个矩阵 [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} [01−10],这个矩阵与任何向量相乘都会使向量逆时针旋转90°。
在理解了矩阵就是向量空间的变换后,我们就能理解单位矩阵使什么意思了,单位矩阵就是原向量空间中基向量本身的集合,我们看单位矩阵 [ 1 0 0 1 ] \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} [1001],只有主对角线上的元素是1,代表各个对应方向上的基向量的长度为1,所以单位矩阵乘以任何向量都等于该向量本身。
如果我们将这里矩阵的特性扩展到三维空间,那么需要记录的基向量就有三个,所以描述三维空间变换的矩阵是 3 × 3 3\times3 3×3的。
复合变换
在上面讲到的线性变换,我们可以使用一个矩阵来表示,即使用变换后基向量的集合来表示一个线性变换。但是一个线性变换也可以理解成由多个线性变换按照一定顺序执行的结果。
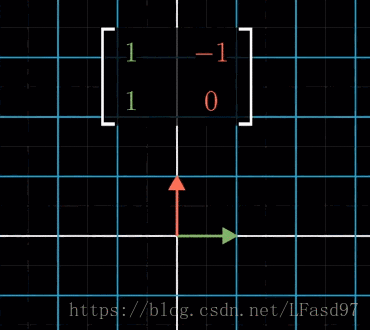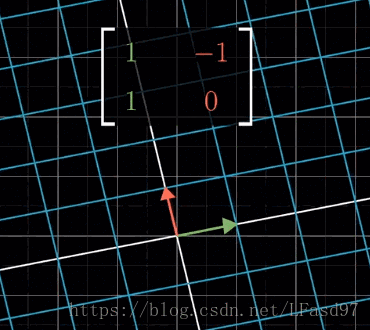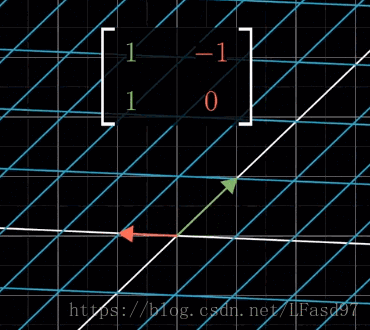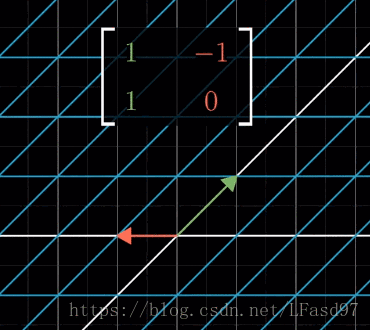
例如,对一个变换 [ 1 − 1 1 0 ] \begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix} [11−10]
我们可以理解成先逆时针旋转90°,然后再往右剪切1个单位,为了方便理解,这里添加了一个向量。
也就是这里的矩阵乘法运算 [ 1 − 1 1 0 ] = [ 1 1 0 1 ] × [ 0 − 1 1 0 ] \begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} [11−10]=[1011]×[01−10]
需要留意的是,这里的矩阵乘法的顺序跟上面图中复合线性变换的顺序是相反的。这相当于函数 f ( g ( v ⃗ ) ) f(g(\vec{v})) f(g(v)),也就是
[ 1 − 1 1 0 ] × [ 2 3 ] = [ 1 1 0 1 ] × [ 0 − 1 1 0 ] × [ 2 3 ] \begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} [11−10]×[23]=[1011]×[01−10]×[23]
上面等式的右边可以理解成 [ 1 1 0 1 ] × ( [ 0 − 1 1 0 ] × [ 2 3 ] ) \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \times \left( \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} \right) [1011]×([01−10]×[23]),对这个逆时针旋转了90°的向量向右剪切一个单位。
理解了复合变换,我们也就能够理解为什么矩阵的乘法中为什么 A × B ≠ B × A A \times B \neq B \times A A×B̸=B×A 了
逆变换
我们已经知道,一个矩阵可以代表一个变换,那么我们可以将逆矩阵理解成逆变换,即对变换后的向量进行逆变换就会变回原来那个向量。矩阵 [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} [01−10] 代表逆时针旋转90°,那它的逆变换就是代表顺时针旋转90°的 [ 0 1 − 1 0 ] \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} [0−110],任何线性变换与它的逆进行复合,最终结果就是一个什么都不做的线性变换,也就是原来基向量的集合,我们称为单位矩阵。
总结
这里我们讨论了线性变换就是对向量空间进行满足两个条件的变换。我们可以使用变换后的基向量来代表一个线性变换,把这些基向量组合起来就形成了矩阵,我们可以使用矩阵向量乘法运算来计算一个对一个向量进行了线性变换后的输出向量。矩阵之间的乘法运算跟线性变换的复合有关,复合变换是不能够打乱变换顺序的,而且它的空间变换顺序是从右到左进行的。逆变换就是一个变换的逆,一个变换与该变换的逆复合就会形成单位矩阵。
小测试
理解了线性变换和复合变换后,我们看看下面这个复合变换的的等式为什么是正确的。
( A × B ) × C = A × ( B × C ) (A \times B) \times C = A \times (B \times C) (A×B)×C=A×(B×C)