- 拓扑排序
- 1. 算法分析
- 1.1 特点分析
- 1.2 使用场景
- 2. 例题
- 2.1 求出拓扑序
- 2.1.1 一般拓扑序
- 2.1.2 求出字典序最大/最小的拓扑序
- 2.2 判断图中是否有环
- 2.3 拓扑排序+dp
- 2.3.1 求最短路\最长路
- 2.3.2 求可达性
- 2.1 求出拓扑序
- 1. 算法分析
拓扑排序
1. 算法分析
1.1 特点分析
拓扑排序可以在线性的时间复杂度 O(n + m) 内完成求出拓扑序的操作,对象是有向无环图。
拓扑图的性质如下:
- 有向图才有拓扑序
- 有向无环图必定存在拓扑序
- 存在拓扑序 <=> 无环
- 有向无环图至少存在一个入度为0的点
- 当前的点只影响后面的状态,所以可以dp处理
1.2 使用场景
拓扑排序,可以支持以下操作:
- 求出拓扑序:
1.1 求一般拓扑序:如果是一般队列,那么求出的为一般的拓扑序
1.2 求字典序最大/最小拓扑序:如果是优先队列,那么求出的是字典序最大/最小拓扑序 - 拓扑序判断环
判断图中是否有环:如果原来的点数==最后拓扑序内的点数,那么拓扑序唯一,无环;否则,有环 - 拓扑序+dp:
3.1 求最短\长路:如果边权全部大于0,那么可以使用拓扑排序找最短路
3.2 求每个点的可达性
2. 例题
2.1 求出拓扑序
2.1.1 一般拓扑序
#include
using namespace std;
int const N = 1e5 + 10;
int e[N], ne[N], h[N], idx, d[N];
int n, m;
vector ans;
// 建立邻接表
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 拓扑排序
void top_sort()
{
queue q; // 维护一个队列
for (int i = 1; i <= n; ++i) if (!d[i]) q.push(i); // 把入度为0的点加入队列
// 当队列不为空时
while (q.size())
{
auto t = q.front(); // 取队头
q.pop(); // 队头出队
ans.push_back(t); // 把这个数字放入答案序列
for (int i = h[t]; i != -1; i = ne[i]) // 枚举所有队头元素相邻的元素
{
int j = e[i];
d[j]--; // 队头元素出队相当于把与队头元素相连的元素的入度减一
if (!d[j]) q.push(j); // 把入度为0的元素放入队列
}
}
if (ans.size() == n) // 输出答案序列
{
for (auto a: ans) printf("%d ", a);
}
else cout << "-1";
}
int main()
{
cin >> n >> m; // 输入点数和边数
memset(h, -1, sizeof h); // 初始化h
for (int i = 0; i < m; ++i) // 读入每条边
{
int a, b;
scanf("%d %d", &a, &b);
add(a, b); // 把b插入a的边表
d[b]++; // b的入度加一
}
top_sort();
return 0;
}
2.1.2 求出字典序最大/最小的拓扑序
#include
using namespace std;
int const N = 1e5 + 10;
int e[N], ne[N], h[N], idx, d[N];
int n, m;
vector ans;
// 建立邻接表
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 拓扑排序
void top_sort()
{
priority_queue, greater> q; // 这里是求字典序最小的拓扑序,如果求字典序最大的,那么改成 priority_queue, less> q;
for (int i = 1; i <= n; ++i) if (!d[i]) q.push(i); // 把入度为0的点加入队列
// 当队列不为空时
while (q.size())
{
auto t = q.top(); // 取队头
q.pop(); // 队头出队
ans.push_back(t); // 把这个数字放入答案序列
for (int i = h[t]; i != -1; i = ne[i]) // 枚举所有队头元素相邻的元素
{
int j = e[i];
d[j]--; // 队头元素出队相当于把与队头元素相连的元素的入度减一
if (!d[j]) q.push(j); // 把入度为0的元素放入队列
}
}
for (int i = 0; i < ans.size(); ++i) {
cout << ans[i];
if (i != ans.size() - 1) cout << " ";
}
cout << endl;
}
int main()
{
while (scanf("%d%d", &n, &m) != EOF) {
memset(d, 0, sizeof d);
ans.clear();
idx= 0;
memset(h, -1, sizeof h); // 初始化h
for (int i = 0; i < m; ++i) // 读入每条边
{
int a, b;
scanf("%d %d", &a, &b);
add(a, b); // 把b插入a的边表
d[b]++; // b的入度加一
}
top_sort();
}
return 0;
}
HDU2857 逃生
题意: t个测试样例,每个测试样例给出n和m,表示n个点、m条边。下面m行给出m条有向边信息a b,表示a->b。求出拓扑序,要求当拓扑序不唯一时,使得序号小的在前。
题解: 让编号小的尽量靠前,这个意思不是字典序最小的拓扑序。解法:反向建图,优先队列(大顶堆)求字典序最大的序列,倒着输出即为本题答案。理解:看上图,我们从1开始走,邻接点3和4,我们不知道后面还有个2,所以不知道3和4先选谁,故正向寻找是错的。既然要求编号小的尽量靠前,那我们可以考虑把编号大的放到后面去。
我们反向走,从最后面往前走,优先走编号大的,也就是字典序最大。最后把序列倒着输出,如此,就满足了本题。
#include
using namespace std;
int const N = 1e5 + 10;
int e[N], ne[N], h[N], idx, d[N];
int n, m, t;
vector ans;
// 建立邻接表
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 拓扑排序
void top_sort()
{
priority_queue, less> q; // 维护一个从大到小的优先队列
for (int i = 1; i <= n; ++i) if (!d[i]) q.push(i); // 把入度为0的点加入队列
// 当队列不为空时
while (q.size())
{
auto t = q.top(); // 取队头
q.pop(); // 队头出队
ans.push_back(t); // 把这个数字放入答案序列
for (int i = h[t]; i != -1; i = ne[i]) // 枚举所有队头元素相邻的元素
{
int j = e[i];
d[j]--; // 队头元素出队相当于把与队头元素相连的元素的入度减一
if (!d[j]) q.push(j); // 把入度为0的元素放入队列
}
}
reverse(ans.begin(), ans.end()); // 反转输出
for (int i = 0; i < ans.size(); ++i) {
cout << ans[i];
if (i != ans.size() - 1) cout << " ";
}
cout << endl;
}
int main()
{
cin >> t;
while (t--) {
scanf("%d%d", &n, &m);
memset(d, 0, sizeof d);
ans.clear();
idx= 0;
memset(h, -1, sizeof h); // 初始化h
for (int i = 0; i < m; ++i) // 读入每条边
{
int a, b;
scanf("%d %d", &a, &b);
add(b, a); // 把b插入a的边表
d[a]++; // b的入度加一
}
top_sort();
}
return 0;
}
2.2 判断图中是否有环
Codeforces Round #656 (Div. 3) E. Directing Edges
题意: 给定t个测试样例,每个测试样例给定n和m,n为图的点数,m为图的边数,给定m条边,每条边为op, a, b。如果op == 1,表示有一条有向边a -> b;如果op == 0,表示a和b之间有一条无向边。现在要求把无向边变成有向边(把a--b变成a->b或b->a),使得最后这m条边没有环。\(\sum_{i=1}^n n、m\) ~ 2e5
题解: 题意可以转换为现在有一张有向图,要求向这张有向图内加入有向边,使得这张有向图没有环,求加边的方法。因此,可以先做一次拓扑排序,求出拓扑序,如果没有拓扑序,说明已经存在环;否则,只需要加入拓扑序小的指向拓扑序大的边即可。(因为想要形成环,必须有回路,则必须a->b,同时b->a,一旦出现拓扑序,说明存在a->b,不存在b->a,因此只要不加入b->a,则不可能出现环)
代码如下:
#include
using namespace std;
int const N = 2e5 + 10;
int t, n, m;
set point;
int e[N * 2], ne[N * 2], idx, h[N];
int d[N], sorted[N];
vector > undirect, direct;
vector ans;
struct Edge{
int op, u, v;
};
vector E;
void top_sort() {
queue q;
for (int i = 1; i <= n; ++i) {
if (!d[i]) {
q.push(i);
}
}
while (q.size()) {
auto t = q.front();
q.pop();
ans.push_back(t);
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
d[j]--;
if (!d[j]) {
q.push(j);
}
}
}
// 记录一下拓扑序内的点的顺序
for (int i = 0; i < ans.size(); ++i) {
sorted[ans[i]] = i + 1;
}
return ;
}
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int main() {
cin >> t;
while (t--) {
memset(h, -1, sizeof h);
memset(d, 0, sizeof d);
idx = 0;
E.clear();
memset(sorted, 0, sizeof sorted);
ans.clear();
cin >> n >> m;
for (int i = 0, op, a, b; i < m; ++i) {
scanf("%d%d%d", &op, &a, &b);
E.push_back({op, a, b});
if (op == 1) {
add(a, b);
d[b]++;
}
}
top_sort();
if (ans.size() != n) {
cout << "NO\n";
continue;
}
cout << "YES\n";
for (int i = 0; i < E.size(); ++i) {
if (E[i].op == 1) {
cout << E[i].u << " " << E[i].v << endl;
}
else {
// 按照拓扑序内顺序小的指向顺序大的
if (sorted[E[i].u] < sorted[E[i].v]) cout << E[i].u << " " << E[i].v << endl;
else cout << E[i].v << " " << E[i].u << endl;
}
}
}
return 0;
}
2.3 拓扑排序+dp
2.3.1 求最短路\最长路
acwing1192奖金
公司按照每个人的贡献给每个人发奖金。奖金存在M对关系,每对关系为a,b,表示a的奖金比b高。每位员工工资最少为100元,问最少需要发多少奖金。
/*
本题是差分约束的简化版,形成的边只有正权边
如果存在正环那么无解,换言之,如果不存在拓扑序则无解,因此可以使用拓扑排序来判断
如果有解,求出拓扑序后,直接按照拓扑序更新最长路即可
*/
#include
using namespace std;
int const N = 1e4 + 10, M = 2e4 + 10;
int n, m;
int din[N], dis[N];
int e[M], ne[M], h[N], idx;
vector ans;
// 拓扑排序
bool topsort()
{
queue q;
for (int i = 1; i <= n; ++i)
if (!din[i]) q.push(i);
while (q.size())
{
auto t = q.front();
q.pop();
ans.push_back(t);
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
din[j]--;
if (!din[j]) q.push(j);
}
}v
return ans.size() == n;
}
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int main()
{
// 建图
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; ++i)
{
int a, b;
scanf("%d %d", &a, &b);
add(b, a);
din[a] ++;
}
// 拓扑排序判断是否有解
if (!topsort())
{
printf("Poor Xed\n");
return 0;
}
// 按照拓扑排序更新最长路
for (int i = 1; i <= n; ++i) dis[i] = 100;
for (int i = 0; i < n; ++i)
{
int t = ans[i];
for (int j = h[t]; ~j; j = ne[j])
{
int k = e[j];
dis[k] = max(dis[k], dis[t] + 1);
}
}
// 计算答案
int ans = 0;
for (int i = 1; i <= n; ++i) ans += dis[i];
cout << ans << endl;
return 0;
}
acwing456车站分级
题意: 一条单向的铁路线上,依次有编号为1, 2, …, n 的n个火车站。每个火车站都有一个级别,最低为1级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站x,则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是5趟车次的运行情况。
其中,前4趟车次均满足要求,而第5趟车次由于停靠了3号火车站(2级)却未停靠途经的6号火车站(亦为2级)而不满足要求。
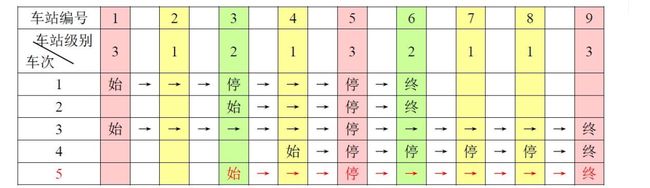
现有m趟车次的运行情况(全部满足要求),试推算这n个火车站至少分为几个不同的级别。1≤n,m≤1000
题解: 很明显,不停靠的站点的优先级一定比停靠的站点的优先级要小,因此不停靠的站点的优先级最小为1,且停靠的站点的优先级>=不停靠的站点的优先级+1,则本题可以转换为一个差分约束问题,且边权大于等于0。(这里不需要tarjan判断是否有正环,因为明确了有解,不可能出现正环,所以直接拓扑排序求拓扑序(tarjan的目的也是缩点完求拓扑序))。本题的另一个难点在于建图,如果直接把不停靠的站点向停靠的站点连一条边,那么建图的复杂度为O(mn^2^)。对于一个二分图,左边的每个点都需要向右边每个点连一条边的建图模型来说,可以设置一个虚拟节点,然后使得左边每个点连向虚拟节点,虚拟节点再向右边每个点连边。这样就把O(n ^ 2)优化到O(n)。
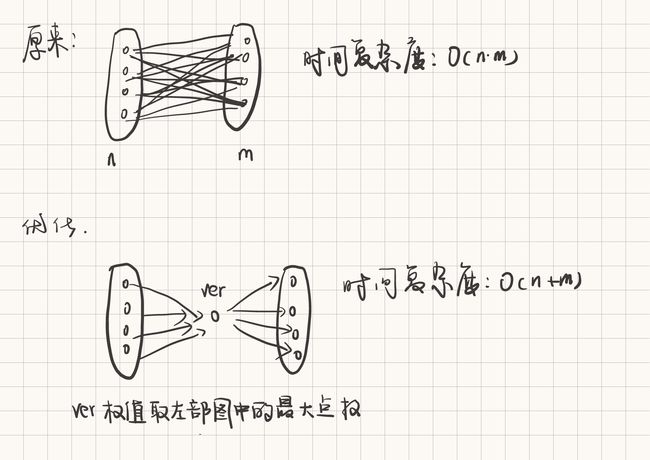
/*
本题是一道差分约束问题,对于每一辆车停靠的站点的优先级一定比没停靠的站点的优先级要高,因此
所有未停靠的站点都可以连一条边到停靠的站点。
但是如果这样建图将会建边平方条,1e8,超时
考虑简单的建边方法:对于每辆车建立一个虚拟节点,这个虚拟节点可以认为是未停靠的车站的最高优先级,
那么对于每个关系b>=a+1则可以从原来的a->b建权值为1的边变化为a向虚拟节点ver建一条边权为0的边,再从ver到b建一条
边权为1的边,这样子就可以把平方的边数降到线性,每辆车最多建立2000条边,总共2e6条边
建图后,由于本题特点保证了一定是一张DAG,所以要求最长路不需要判正环,直接拓扑排序后得到顺序,然后dp求最长路即可
*/
#include
using namespace std;
int const N = 2e3 + 10, M = 2e6 + 10;
int n, m;
int e[M], ne[M], h[N], w[M], idx;
int din[N], st[N], dis[N];
vector ans;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
// 拓扑排序
void topsort()
{
queue q;
for (int i = 1; i <= n + m; ++i) if (!din[i]) q.push(i);
while (q.size())
{
auto t = q.front();
q.pop();
ans.push_back(t);
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
din[j]--;
if (!din[j]) q.push(j);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i <= m; ++i)
{
// 建图(加入虚节点,平方->线性)
memset(st, 0, sizeof st);
int cnt, start = n, end = 1, ver = n + i; // start记录最小的点,end记录最大的点,ver记录虚拟节点
cin >> cnt;
for (int i = 0; i < cnt; ++i)
{
int t;
cin >> t;
st[t] = 1;
start = min(start, t);
end = max(end, t);
}
// 把a->b的边拆成a->ver和ver->b
for (int j = start; j <= end; ++j)
{
if (st[j]) add(ver, j, 1), din[j]++;
else add(j, ver, 0), din[ver]++;
}
}
// 拓扑排序得到更新的顺序
topsort();
// dp求最大值
for (int i = 1; i <= n; ++i) dis[i] = 1;
for (int i = 0; i < ans.size(); ++i)
{
int k = ans[i];
for (int j = h[k]; ~j; j = ne[j])
{
int t = e[j];
dis[t] = max(dis[t], dis[k] + w[j]);
}
}
int res = 0;
for (int i = 1; i <= n; ++i) res = max(res, dis[i]);
cout << res << endl;
return 0;
}
2.3.2 求可达性
acwing164可达性统计
给定一张N个点M条边的有向无环图,分别统计从每个点出发能够到达的点的数量。第一行两个整数N,M,接下来M行每行两个整数x,y,表示从x到y的一条有向边。输出共N行,表示每个点能够到达的点的数量。1≤N,M≤30000
/*
因为是有向无环图,所以当前状态只影响后面的状态,所以可以使用dp的思想处理
因此,先做一次拓扑排序,得到拓扑序,而后使用逆拓扑序倒着向前更新每个点的可达性
具体更新的时候可以使用一个bitset即可维护当前每个点的可达状态
*/
#include
using namespace std;
int const N = 3e4 + 10;
int e[N], ne[N], idx, h[N];
int n, m, d[N];
bitset f[N];
vector ans;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void top_sort() {
queue q;
for (int i = 1; i <= n; ++i) if (!d[i]) q.push(i);
while (!q.empty()) {
auto t = q.front();
q.pop();
ans.push_back(t);
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
d[j]--;
if (!d[j]) q.push(j);
}
}
return ;
}
int main(){
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1, a, b; i <= m; ++i) {
scanf("%d%d", &a, &b);
d[b] ++;
add(a, b);
}
// 求出拓扑序
top_sort();
// 倒着更新求出可达性
for (int i = ans.size() - 1; i >= 0; --i) {
int j = ans[i]; // 当前这个点
f[j][j] = 1; // 当前这个点到自己是可达的
for (int k = h[j]; ~k; k = ne[k]) {
int t = e[k]; // j能够遍历到的点是t
f[j] |= f[t]; // j的状态受t影响
}
}
for (int i = 1; i <= n; ++i) cout << f[i].count() << endl;
return 0;
}