Vulkan_曲面细分(Tessellation Shader)
曲面细分
本部分我们主要来看一下图形管线中的可选功能:曲面细分。
曲面细分靠近管线的最前端,紧挨着顶点着色器之后,它是以图元片(patch)作为输入:每一个都是一个用顶点表示的控制点集合,并把片段分解成更小、更简单的片元,比如点线三角形,从而以正常的方式在管线余下的阶段中渲染。
曲面细分是一个管线中可灵活配置的固有功能模块,并且在它的一前一后有两个着色器阶段:表面细分控制着色器(tessellation control shader)和表面细分评估着色器(tessellation evaluation shader)。
一、vulkan实现
本场景仅是加载一个简单的模型具体步骤不在赘述,基础的顶点和片元着色器非常简单如下:
顶点着色器
#version 450
layout (location = 0) in vec3 inPos;
void main(void)
{
gl_Position = vec4(inPos.xyz, 1.0);
}
片元着色器
#version 450
layout (location = 0) out vec4 outFragColor;
void main()
{
outFragColor.rgb = color.rgb * 1.5;
}
在创建管线的时候注意使用的是线框模式:
VkPipelineRasterizationStateCreateInfo pipelineRasterizationStateCreateInfo {};
pipelineRasterizationStateCreateInfo.polygonMode = VK_POLYGON_MODE_LINE;
此外还需注意的是在创建图形管线的时候将结构体VkPipelineTessellationStateCreateInfo 填充如下:
VkPipelineTessellationStateCreateInfo pipelineTessellationStateCreateInfo {};
pipelineTessellationStateCreateInfo.sType = VK_STRUCTURE_TYPE_PIPELINE_TESSELLATION_STATE_CREATE_INFO;
pipelineTessellationStateCreateInfo.patchControlPoints = 3;
其中patchControlPoints会影响曲面细分状态。
最后就是将基础的管线和曲面细分着色器加载并传入管线:
// Load shaders
std::array<VkPipelineShaderStageCreateInfo, 4> shaderStages;
shaderStages[0] = loadShader("shaders/tessellation/base.vert.spv", VK_SHADER_STAGE_VERTEX_BIT);
shaderStages[1] = loadShader("shaders/tessellation/base.frag.spv", VK_SHADER_STAGE_FRAGMENT_BIT);
shaderStages[2] = loadShader("shaders/tessellation/pntriangles.tesc.spv", VK_SHADER_STAGE_TESSELLATION_CONTROL_BIT);
shaderStages[3] = loadShader("shaders/tessellation/pntriangles.tese.spv", VK_SHADER_STAGE_TESSELLATION_EVALUATION_BIT);
接下来我们来具体详述着色器,在此之前我们先来介绍下曲面细分中用到经典PN Triangles算法。
二、PN Triangles算法
PN triangle是一个特殊的贝塞尔曲面,它的表示形式为:
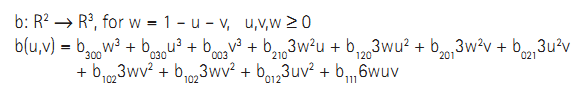
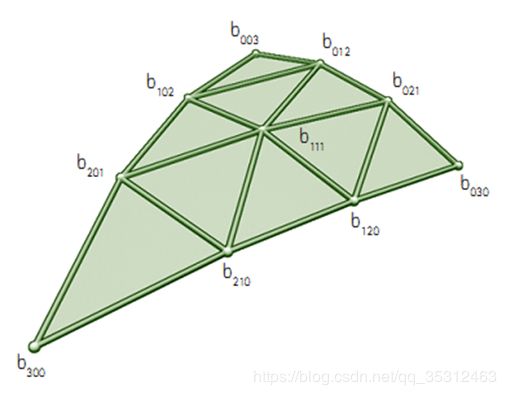
u,v, w是重心坐标,bxyz就是控制点,其中u+v+w=1,控制点的位置如下,看以看出来,b003, b030,b300就是三角形的三个顶点控制点,根据这三个控制点位置和法向,我们就可以计算出其它控制点的位置。
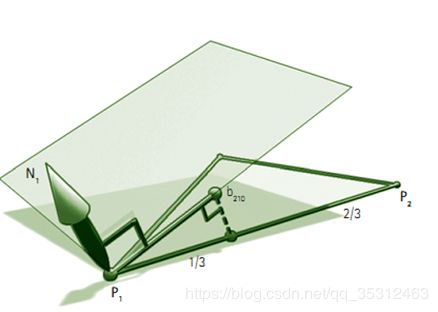

PN triangles的法向通过下面的方法计算得到:


从上述的计算原理我们可以看出,PN triangle的控制点信息是依据输入三角形的顶点位置信息和法线信息计算求得,而它的质心坐标则是通过细分着色器来进行插值并输出。
三、曲面细分控制着色器(tessellation control shader)
表面细分控制着色器(tessellation control shader),它负责处理图元的控制点,设置每个图元片的某些参数,然后将控制权交给固定功能细分模块。该模块获取到图元后,会把图元分解成基本的点线三角形,最终把生成的顶点数据送入评估着色器。
#version 450
// PN数据
struct PnPatch
{
float b210;
float b120;
float b021;
float b012;
float b102;
float b201;
float b111;
float n110;
float n011;
float n101;
};
// 细分等级可控
layout (binding = 0) uniform UBO
{
float tessLevel;
} ubo;
//设置三角形输出
layout(vertices=3) out;
layout(location = 0) in vec3 inNormal[];
layout(location = 1) in vec2 inUV[];
//location对应上三角形输出
layout(location = 0) out vec3 outNormal[3];
layout(location = 3) out vec2 outUV[3];
layout(location = 6) out PnPatch outPatch[3];
float wij(int i, int j)
{
return dot(gl_in[j].gl_Position.xyz - gl_in[i].gl_Position.xyz, inNormal[i]);
}
float vij(int i, int j)
{
vec3 Pj_minus_Pi = gl_in[j].gl_Position.xyz
- gl_in[i].gl_Position.xyz;
vec3 Ni_plus_Nj = inNormal[i]+inNormal[j];
return 2.0*dot(Pj_minus_Pi, Ni_plus_Nj)/dot(Pj_minus_Pi, Pj_minus_Pi);
}
void main()
{
// 获取数据
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
outNormal[gl_InvocationID] = inNormal[gl_InvocationID];
outUV[gl_InvocationID] = inUV[gl_InvocationID];
// 初始化
float P0 = gl_in[0].gl_Position[gl_InvocationID];
float P1 = gl_in[1].gl_Position[gl_InvocationID];
float P2 = gl_in[2].gl_Position[gl_InvocationID];
float N0 = inNormal[0][gl_InvocationID];
float N1 = inNormal[1][gl_InvocationID];
float N2 = inNormal[2][gl_InvocationID];
// 计算控制点
outPatch[gl_InvocationID].b210 = (2.0*P0 + P1 - wij(0,1)*N0)/3.0;
outPatch[gl_InvocationID].b120 = (2.0*P1 + P0 - wij(1,0)*N1)/3.0;
outPatch[gl_InvocationID].b021 = (2.0*P1 + P2 - wij(1,2)*N1)/3.0;
outPatch[gl_InvocationID].b012 = (2.0*P2 + P1 - wij(2,1)*N2)/3.0;
outPatch[gl_InvocationID].b102 = (2.0*P2 + P0 - wij(2,0)*N2)/3.0;
outPatch[gl_InvocationID].b201 = (2.0*P0 + P2 - wij(0,2)*N0)/3.0;
float E = ( outPatch[gl_InvocationID].b210
+ outPatch[gl_InvocationID].b120
+ outPatch[gl_InvocationID].b021
+ outPatch[gl_InvocationID].b012
+ outPatch[gl_InvocationID].b102
+ outPatch[gl_InvocationID].b201 ) / 6.0;
float V = (P0 + P1 + P2)/3.0;
outPatch[gl_InvocationID].b111 = E + (E - V)*0.5;
outPatch[gl_InvocationID].n110 = N0+N1-vij(0,1)*(P1-P0);
outPatch[gl_InvocationID].n011 = N1+N2-vij(1,2)*(P2-P1);
outPatch[gl_InvocationID].n101 = N2+N0-vij(2,0)*(P0-P2);
// 设置细分等级
gl_TessLevelOuter[gl_InvocationID] = ubo.tessLevel;
gl_TessLevelInner[0] = ubo.tessLevel;
}
其中我们使用了PN Triangles算法为低精度多边形模型添加细节。在设置细分等级精度之前我们可以看到,我们根据PN Triangles算法将所需数据皆计算好,并传递给评估着色器使用。
三角形内外部细分示意图如下: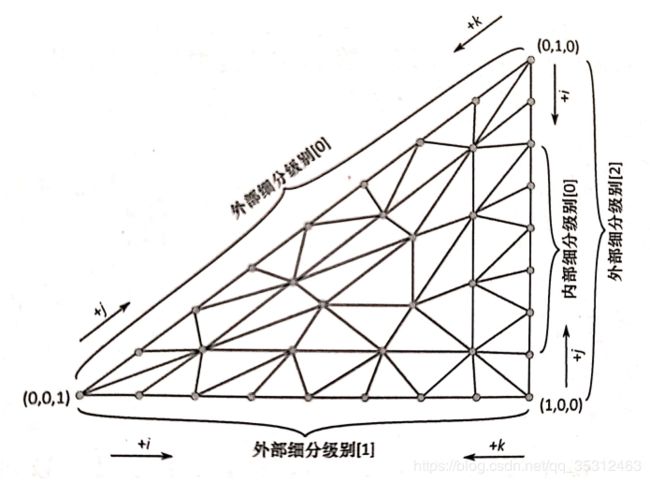
相关细分着色器内置字段及定义:
-
gl_out数组具有相同的结构体成员,不过数组大小与gl_in不同,它是由gl_PatchVerticesOut来指定的。而这个值则是在细分曲面控制器中的out这一layout限定符中设置。此外,以下标量值用于确定正在被着色的图元和输出顶点:
-
gl_InvocationID:当前细分曲面着色器的输出顶点的调用索引
-
gl_PrimitiveID:当前输入patch的图元索引
-
gl_PatchVerticesIn:输入patch中的顶点个数,它作为gl_in数组变量中的元素个数
-
gl_PatchVerticesOut:输出patch中的顶点个数,它作为gl_out数组变量中的元素个数
如果我们需要额外的基于每个顶点的属性值,或为输入或为输出,那么这需要在我们的细分曲面控制着色器中将它们声明为in或out数组。一个输入数组的大小需要与输入patch大小相同,或者可以被声明为缺省大小的,这样Vulkan将会为其所有值适当地分配空间。类似地,每个顶点的输出属性需要与输出patch中的顶点个数相一致,也可以为输出属性声明为缺省大小的。输出属性值将会被传递到细分曲面计算着色器,作为其输入属性值。
四、曲面细分评估着色器(tessellation evaluation shader)
表面细分控制着色器(tessellation control shader),它的作用和顶点着色器类似,只不过它处理的是所有新生成的点。
#version 450
// PN数据
struct PnPatch
{
float b210;
float b120;
float b021;
float b012;
float b102;
float b201;
float b111;
float n110;
float n011;
float n101;
};
layout (binding = 1) uniform UBO
{
mat4 projection;
mat4 model;
float tessAlpha;
} ubo;
//triangles:使用重心坐标的一个三角形域;域坐标:带有范围在[0, 1]内的a、b、c三个值的坐标(a, b, c),这里a+b+c=1。
//fractional_odd_spacing:值被裁减到[1, max-1]范围内,然后取整到下一个最大奇整数值n。边然后被划分为n-2条等长部分,以及两个剩余部分,每个在一端,剩余部分长度可能比其它长度要短,
//ccw:表面细分环绕顺序:逆时针方向
layout(triangles, fractional_odd_spacing, ccw) in;
layout(location = 0) in vec3 iNormal[];
layout(location = 3) in vec2 iTexCoord[];
layout(location = 6) in PnPatch iPnPatch[];
layout(location = 0) out vec3 oNormal;
layout(location = 1) out vec2 oTexCoord;
#define uvw gl_TessCoord
void main()
{
vec3 uvwSquared = uvw * uvw;
vec3 uvwCubed = uvwSquared * uvw;
// 提取控制点
vec3 b210 = vec3(iPnPatch[0].b210, iPnPatch[1].b210, iPnPatch[2].b210);
vec3 b120 = vec3(iPnPatch[0].b120, iPnPatch[1].b120, iPnPatch[2].b120);
vec3 b021 = vec3(iPnPatch[0].b021, iPnPatch[1].b021, iPnPatch[2].b021);
vec3 b012 = vec3(iPnPatch[0].b012, iPnPatch[1].b012, iPnPatch[2].b012);
vec3 b102 = vec3(iPnPatch[0].b102, iPnPatch[1].b102, iPnPatch[2].b102);
vec3 b201 = vec3(iPnPatch[0].b201, iPnPatch[1].b201, iPnPatch[2].b201);
vec3 b111 = vec3(iPnPatch[0].b111, iPnPatch[1].b111, iPnPatch[2].b111);
// 提取控制法线
vec3 n110 = normalize(vec3(iPnPatch[0].n110, iPnPatch[1].n110, iPnPatch[2].n110));
vec3 n011 = normalize(vec3(iPnPatch[0].n011, iPnPatch[1].n011, iPnPatch[2].n011));
vec3 n101 = normalize(vec3(iPnPatch[0].n101, iPnPatch[1].n101, iPnPatch[2].n101));
// 计算texcoords
oTexCoord = gl_TessCoord[2]*iTexCoord[0] + gl_TessCoord[0]*iTexCoord[1] + gl_TessCoord[1]*iTexCoord[2];
// normal
// 重心法线
vec3 barNormal = gl_TessCoord[2]*iNormal[0] + gl_TessCoord[0]*iNormal[1] + gl_TessCoord[1]*iNormal[2];
vec3 pnNormal = iNormal[0]*uvwSquared[2] + iNormal[1]*uvwSquared[0] + iNormal[2]*uvwSquared[1]
+ n110*uvw[2]*uvw[0] + n011*uvw[0]*uvw[1]+ n101*uvw[2]*uvw[1];
oNormal = ubo.tessAlpha*pnNormal + (1.0-ubo.tessAlpha) * barNormal;
// 计算插值位置
vec3 barPos = gl_TessCoord[2]*gl_in[0].gl_Position.xyz
+ gl_TessCoord[0]*gl_in[1].gl_Position.xyz
+ gl_TessCoord[1]*gl_in[2].gl_Position.xyz;
// 节省一些计算
uvwSquared *= 3.0;
// 计算PN的位置
vec3 pnPos = gl_in[0].gl_Position.xyz*uvwCubed[2]
+ gl_in[1].gl_Position.xyz*uvwCubed[0]
+ gl_in[2].gl_Position.xyz*uvwCubed[1]
+ b210*uvwSquared[2]*uvw[0]
+ b120*uvwSquared[0]*uvw[2]
+ b201*uvwSquared[2]*uvw[1]
+ b021*uvwSquared[0]*uvw[1]
+ b102*uvwSquared[1]*uvw[2]
+ b012*uvwSquared[1]*uvw[0]
+ b111*6.0*uvw[0]*uvw[1]*uvw[2];
// 最终位置和法线
vec3 finalPos = (1.0-ubo.tessAlpha)*barPos + ubo.tessAlpha*pnPos;
gl_Position = ubo.projection * ubo.model * vec4(finalPos,1.0);
}
在表面细分控制着色器处理好之后,我们运行可以看到如下效果(此时内部和外部细分等级都是1(uboTessControl.tessLevel = 1)):
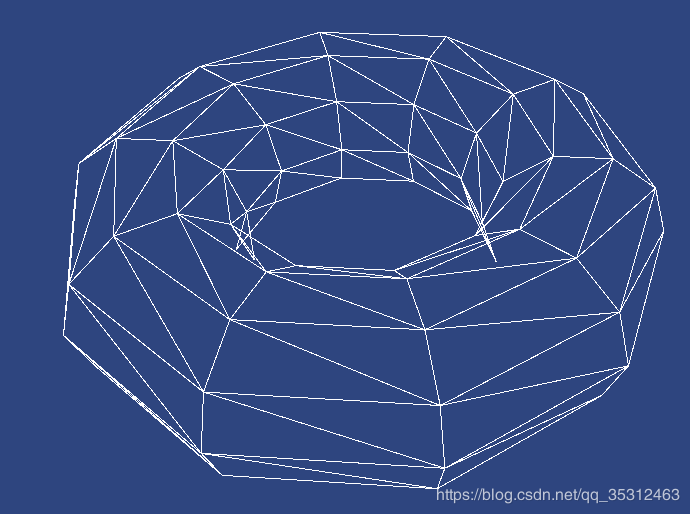
你可以设置不同的细分等级来查看对应的曲面细分程度及PN Triangles效果:
uboTessControl.tessLevel = 2:
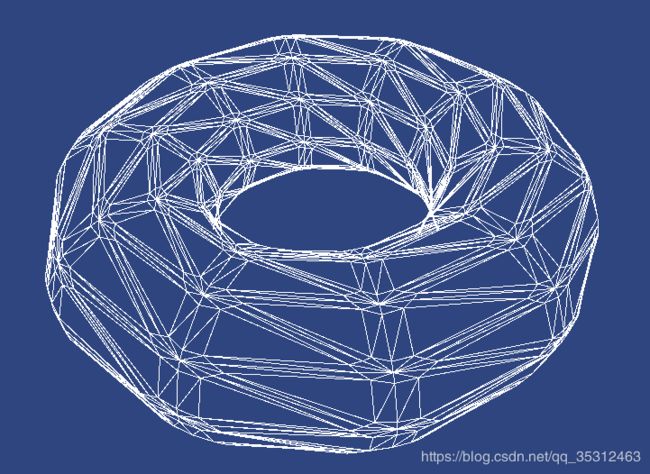
uboTessControl.tessLevel = 5:

uboTessControl.tessLevel = 13:
