聚类分析与判别分析十题_数学建模系列
聚类分析与判别分析习题_数学建模系列
1.
【问题描述】:
5位代理商对某种产品的四种指标评分如下:
| x1 | x2 | x3 | x4 | |
|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 32 |
| 2 | 5 | 2 | 5 | 38 |
| 3 | 3 | 3 | 7 | 30 |
| 4 | 1 | 2 | 3 | 16 |
| 5 | 4 | 3 | 2 | 30 |
其中, x1 , x2 , x3 为态度测度,共有17个分值, x4 为兴趣测度,取值为1140.求出其绝对值距离矩阵,平方和距离矩阵。
【解析】:
编写如下的Matlab程序:(为latex版本,后文省略排版代码)
\begin{verbatim}
X = [2 4 6 32;
5 2 5 38;
3 3 7 30;
1 2 3 16;
4 3 2 30];
D1 = pdist(X, 'cityblock')
D2 = pdist(X, 'euclidean')
\end{verbatim}于是得到如下的计算结果:
(1)绝对值距离矩阵:
D1=⎛⎝⎜⎜⎜⎜⎜012522912013281351302162228210199136190⎞⎠⎟⎟⎟⎟⎟
(2)平方和距离矩阵:
D2=⎛⎝⎜⎜⎜⎜⎜07.07112.645816.43175.00007.071108.544022.44998.66032.64588.5440014.73095.099016.431722.449914.7309014.38755.00008.66035.099014.38750⎞⎠⎟⎟⎟⎟⎟
2.
【问题描述】:
检测某类产品的重量,抽了六个样品,每个样品只测了一个指标,分别为1,2,3,6,9,11.试用最短距离法,重心法进行聚类分析。
【解析】:
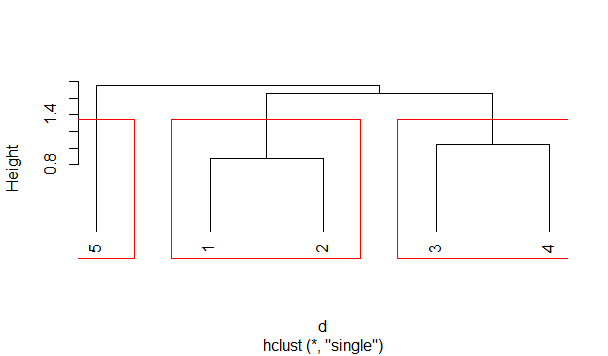
(1)按照最短距离法进行聚类分析。编写如下的R语言程序:
X <- data.frame(
x1 = c(1, 2, 3, 6, 9, 11),
row.names = c("1", "2", "3", "4", "5", "6")
)
d <- dist(scale(X), method = 'euclidean')
heatmap(as.matrix(d),labRow = rownames(d), labCol = colnames(d))
kinds <- 3
model1 <- hclust(d, method = 'single')
result <- cutree(model1, k = kinds)
plot(model1, -1)
rect.hclust(model1, k = kinds, border = "red")
↑首先得到的是样本之间的相关关系,颜色越深表示这两个样本之间的关系越近,亦可能属于同一类。
(下面为latex绘图代码片,后文略)
\begin{figure}[h]
\centering
\includegraphics[width=*0.75*\textwidth]{*5.png*}
\end{figure}所以将样本划分为: {1,2,3,4} 、 {5,6} 。
(2)按照重心法进行聚类分析。编写如下的R语言程序:
kinds <- 2
model1 <- hclust(d, method = 'centroid')
result <- cutree(model1, k = kinds)
plot(model1, -1)
rect.hclust(model1, k = kinds, border = "red")所以将样本划分为: {1,2,3} 、 {4,5,6} 。
3.
【问题描述】:
某店五个售货员的销售量 x1 与教育水平 x2 之间的评分表如下,试用最短距离法做聚类分析
| x1 | x2 | |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 6 | 3 |
| 4 | 8 | 2 |
| 5 | 8 | 0 |
【解析】:
编写如下的R语言程序:
X <- data.frame(
x1 = c(1, 1, 6, 8, 8),
x2 = c(1, 2, 3, 2, 0),
row.names = c("1", "2", "3", "4", "5")
)
d <- dist(scale(X), method = 'euclidean')
heatmap(as.matrix(d),labRow = rownames(d), labCol = colnames(d))
kinds <- 3
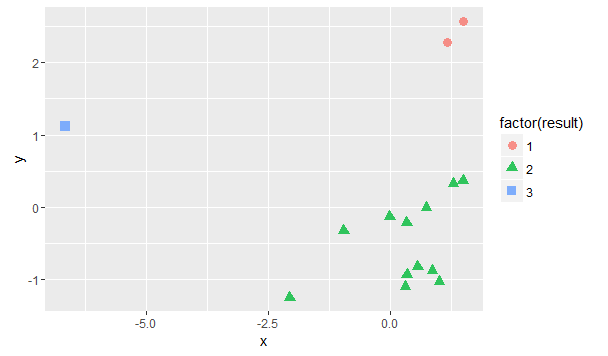
model1 <- hclust(d, method = 'single')
result <- cutree(model1, k = kinds)
plclust(model1, -1)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result),shape = factor(result)))
↑首先得到的是样本之间的相关关系,颜色越深表示这两个样本之间的关系越近,亦可能属于同一类。
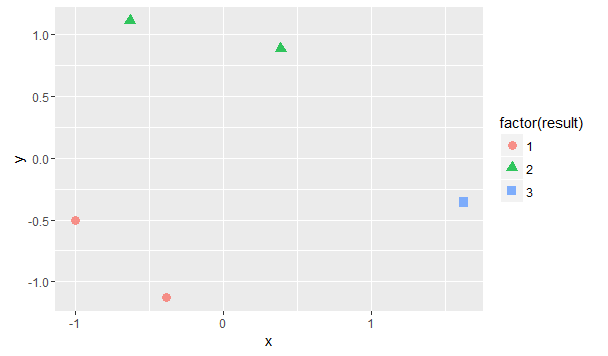
↑为了更直观的表示出3类之间的关系,利用经典MDS对样本数据进行变换,在二维平面上绘制出散点图。
可见,按照3类进行划分是合理的。所以将样本划分为: {1,2} 、 {3,4} 、 {5} 。
4.
【问题描述】:
下面给出七个样品两两之间的欧氏距离矩阵
D=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜12345671047121819212038141517305111214406179501360270⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
试分别用最小距离法、最大距离法、重心举例法进行聚类,并画出系谱图。
【解析】:
编写如下的Matlab程序:
d = [4, 7, 12, 18, 19, 21, 3, 8, 14, 15, 17, 5, 11, 12, 14, 6, 7, 9, 1, 3, 2];
z1 = linkage(d);
z2 = linkage(d, 'complete');
z3 = linkage(d, 'average');
k = 3;
figure(1);
H1 = dendrogram(z1);
T1 = cluster(z1, k)
figure(2);
H2 = dendrogram(z2);
T2 = cluster(z2, k)
figure(3);
H3 = dendrogram(z3);
T3 = cluster(z3, k)(1)最小距离法得到的聚类结果为: {1,2,3} 、 {4} 、 {5,6,7} 。绘制的谱系聚类图,如下:
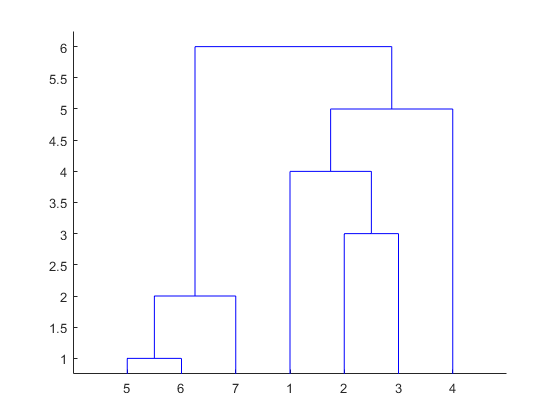
(2)最大距离法得到的聚类结果为: {1,2,3} 、 {4} 、 {5,6,7} 。绘制的谱系聚类图,如下:

(3)重心距离法得到的聚类结果为: {1,2,3} 、 {4} 、 {5,6,7} 。绘制的谱系聚类图,如下:

5.
【问题描述】:
华北五站(北京、天津、营口、太远、石家庄)1968年(及1969年)7、8月份降水量( Y )作预报。
- (1)根据专业的统计分析 Y 主要取决于下列因子:
- X_1:上海4月份平均气温,
- X_2:北京三月份降水总量,
- X_3:5月份地磁 Ci 指数,
- X_4:4月份500 mbW 环流型日数
(2)1961-1967年的历史数据如下:
| 时间 | Y/mm | x1 | x2 | x3 | x4 |
|---|---|---|---|---|---|
| 1961 | 410 | 14.8 | 20.1 | 0.69 | 13 |
| 1962 | 255 | 12.5 | 2.3 | 0.36 | 4 |
| 1963 | 527 | 14.5 | 12.4 | 0.69 | 12 |
| 1964 | 510 | 16.4 | 10.6 | 0.58 | 26 |
| 1965 | 226 | 12.2 | 0.3 | 0.35 | 4 |
| 1966 | 456 | 13.8 | 12.3 | 0.42 | 23 |
| 1967 | 389 | 13.6 | 7.7 | 0.82 | 25 |
| 1968 | 13.7 | 0.6 | 0.68 | 12.5 | |
| 1969 | 14.2 | 16.5 | 0.65 | 15 |
【解析】:
首先,编写如下的R语言程序,检测二变量间关系。
X1 <- c(14.8, 12.5, 14.5, 16.4, 12.2, 13.8, 13.6)
X2 <- c(20.1, 2.3, 12.4, 10.6, 0.3, 12.3, 7.7)
X3 <- c(0.69, 0.36, 0.69, 0.58, 0.35, 0.42, 0.82)
X4 <- c(13, 4, 12, 26, 4, 23, 25)
Y <- c(410, 255, 527, 510, 226, 456, 389)
testData <- data.frame(X1, X2, X3, X4, Y)
cor(testData)
library(car)
scatterplotMatrix(testData, spread = FALSE, lty.smooth = 2, main = "Scatter Plot Matrix")得到相关系数矩阵如下:
| X1 | X2 | X3 | X4 | Y | |
|---|---|---|---|---|---|
| X1 | 1.0000000 | 0.6950138 | 0.5142621 | 0.6627185 | 0.8497245 |
| X2 | 0.6950138 | 1.0000000 | 0.5762508 | 0.4386373 | 0.7227803 |
| X3 | 0.5142621 | 0.5762508 | 1.0000000 | 0.5283724 | 0.5735971 |
| X4 | 0.6627185 | 0.4386373 | 0.5283724 | 1.0000000 | 0.6979025 |
接着,利用R语言程序进行多元线性拟合。
fit <- lm(Y ~ X1 + X2 + X3 + X4, data = testData)
summary(fit)
vif(fit)得到回归分析表:
lm(formula = Y ~ X1 + X2 + X3 + X4, data = testData)
Residuals:
1 2 3 4 5 6 7
-63.59 -11.54 101.28 -22.20 -19.41 37.15 -21.69
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -278.856 541.448 -0.515 0.658
X1 40.935 44.060 0.929 0.451
X2 4.251 8.506 0.500 0.667
X3 34.616 269.756 0.128 0.910
X4 2.869 5.642 0.508 0.662
Residual standard error: 92.62 on 2 degrees of freedom
Multiple R-squared: 0.7928, Adjusted R-squared: 0.3783
F-statistic: 1.913 on 4 and 2 DF, p-value: 0.3715以及方差膨胀因c:
X1 X2 X3 X4
2.791265 2.272406 1.743121 2.001629说明该模型存在多重共线性。
于是,将 X3 剔除,再进行多元拟合:
fit <- lm(Y ~ X1 + X2 + X4, data = testData)
summary(fit)
vif(fit)得到回归分析表:
lm(formula = Y ~ X1 + X2 + X4, data = testData)
Residuals:
1 2 3 4 5 6 7
-62.90 -12.92 105.41 -24.26 -20.33 29.29 -14.28
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -265.627 435.785 -0.610 0.585
X1 40.830 36.116 1.131 0.340
X2 4.669 6.439 0.725 0.521
X4 3.106 4.369 0.711 0.528
Residual standard error: 75.93 on 3 degrees of freedom
Multiple R-squared: 0.791, Adjusted R-squared: 0.5821
F-statistic: 3.786 on 3 and 3 DF, p-value: 0.1516以及方差膨胀因子:
X1 X2 X4
2.790316 1.937625 1.786125说明该模型存在多重共线性。
于是,将 X4 剔除,再进行多元拟合:
fit <- lm(Y ~ X1 + X2, data = testData)
summary(fit)
vif(fit)得到回归分析表:
lm(formula = Y ~ X1 + X2, data = testData)
Residuals:
1 2 3 4 5 6 7
-79.79 -28.38 88.25 -25.28 -31.89 56.23 20.86
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -415.076 357.354 -1.162 0.310
X1 55.051 28.151 1.956 0.122
X2 4.483 6.023 0.744 0.498
Residual standard error: 71.08 on 4 degrees of freedom
Multiple R-squared: 0.7558, Adjusted R-squared: 0.6338
F-statistic: 6.191 on 2 and 4 DF, p-value: 0.05961以及方差膨胀因子:
X1 X2
1.934401 1.934401说明该模型不存在多重共线性。
若将 X2 剔除,再进行多元拟合:
fit <- lm(Y ~ X1, data = testData)
summary(fit)得到回归分析表:
Call:
lm(formula = Y ~ X1, data = testData)
Residuals:
1 2 3 4 5 6 7
-43.82 -38.71 94.06 -55.20 -46.83 71.79 18.71
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -576.45 271.09 -2.126 0.0868 .
X1 69.61 19.32 3.604 0.0155 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 67.84 on 5 degrees of freedom
Multiple R-squared: 0.722, Adjusted R-squared: 0.6664
F-statistic: 12.99 on 1 and 5 DF, p-value: 0.01548此时,可以建立回归模型: Y=0.0868+0.0155X1 。散点图和拟合直线如下所示:
于是,在置信水平为 95% 下,1968年华北五站7、8月份降水量预测值为377.2479,置信区间为 [309.9719,444.5238] ;1969年华北五站7、8月份降水量预测值为412.0544,置信区间为 [345.1723,478.9366] 。
6.
下表是15个上市公司2001年的一些主要财务指标,使用系统聚类法和K-均值法分别对这些公司进行聚类,并对结果进行比较分析。其中, x1 :公司编号, x2 :净资产收益率, x3 :每股净利润, x4 :总资产周转率, x5 :资产负债率, x6 :流动负债比率, x7 :每股净资产, x8 :净利润增长率, x9 :总资产增长率
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
|---|---|---|---|---|---|---|---|---|
| 1 | 11.09 | 0.21 | 0.05 | 96.98 | 70.53 | 1.86 | -44.04 | 81.99 |
| 2 | 11.96 | 0.59 | 0.74 | 51.78 | 90.73 | 4.95 | 7.02 | 16.11 |
| 3 | 0 | 0.03 | 0.03 | 181.99 | 100 | -2.98 | 103.33 | 21.18 |
| 4 | 11.58 | 0.13 | 0.17 | 46.07 | 92.18 | 1.14 | 6.55 | -56.32 |
| 5 | -6.19 | -0.09 | 0.03 | 43.3 | 82.24 | 1.52 | -1713.5 | -3.36 |
| 6 | 10 | 0.47 | 0.48 | 68.4 | 86 | 4.7 | -11.56 | 0.85 |
| 7 | 10.49 | 0.11 | 0.35 | 82.98 | 99.87 | 1.02 | 100.23 | 30.32 |
| 8 | 11.12 | -1.69 | 0.12 | 132.14 | 100 | -0.66 | -4454.39 | -62.75 |
| 9 | 3.41 | 0.04 | 0.2 | 67.86 | 98.51 | 1.25 | -11.25 | -11.43 |
| 10 | 1.16 | 0.01 | 0.54 | 43.7 | 100 | 1.03 | -87.18 | -7.41 |
| 11 | 30.22 | 0.16 | 0.4 | 87.36 | 94.88 | 0.53 | 729.41 | -9.97 |
| 12 | 8.19 | 0.22 | 0.38 | 30.31 | 100 | 2.73 | -12.31 | -2.77 |
| 13 | 95.79 | -5.2 | 0.5 | 252.34 | 99.34 | -5.42 | -9816.52 | -46.82 |
| 14 | 16.55 | 0.35 | 0.93 | 72.31 | 84.05 | 2.14 | 115.95 | 123.41 |
| 15 | -24.18 | -1.16 | 0.79 | 56.26 | 97.8 | 4.81 | -533.89 | -27.74 |
【解析】:
(1)层次聚类法:编写如下的R语言程序:
X <- data.frame(
x2 = c(11.09, 11.96, 0, 11.58, -6.19, 10, 10.49, 11.12, 3.41, 1.16, 30.22, 8.19, 95.79, 16.55, -24.18),
x3 = c(0.21, 0.59, 0.03, 0.13, -0.09, 0.47, 0.11, -1.69, 0.04, 0.01,0.16, 0.22, -5.2, 0.35, -1.16),
x4 = c(0.05, 0.74, 0.03, 0.17, 0.03, 0.48, 0.35, 0.12, 0.2, 0.54, 0.4,0.38, 0.5, 0.93, 0.79),
x5 = c(96.98, 51.78, 181.99, 46.07, 43.3, 68.4, 82.98, 132.14, 67.86,43.7, 87.36, 30.31, 252.34, 72.31, 56.26),
x6 = c(70.53, 90.73, 100, 92.18, 82.24, 86, 99.87, 100, 98.51, 100,94.88, 100, 99.34, 84.05, 97.8),
x7 = c(1.86, 4.95, -2.98, 1.14, 1.52, 4.7, 1.02, -0.66, 1.25, 1.03,0.53, 2.73, -5.42, 2.14, 4.81),
x8 = c(-44.04, 7.02, 103.33, 6.55, -1713.5, -11.56, 100.23, -4454.39,-11.25, -87.18, 729.41, -12.31, -9816.52, 115.95, -533.89),
x9 = c(81.99, 16.11, 21.18, -56.32, -3.36, 0.85, 30.32, -62.75,-11.43, -7.41, -9.97, -2.77, -46.82, 123.41, -27.74),
row.names = c("1", "2", "3", "4", "5", "6", "7", "8", "9", "10","11", "12", "13", "14", "15")
)
d <- dist(scale(X), method = 'euclidean')
heatmap(as.matrix(d),labRow = rownames(d), labCol = colnames(d))
kinds <- 3
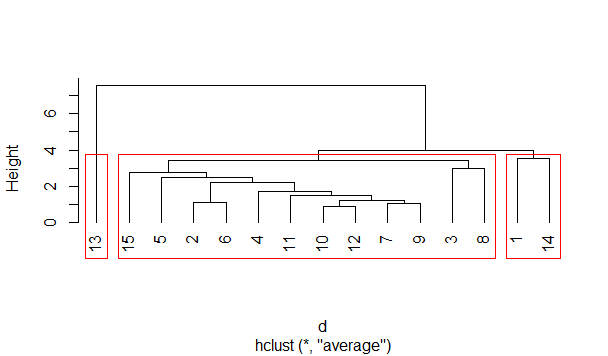
model1 <- hclust(d, method = 'average')
result <- cutree(model1, k = kinds)
plclust(model1, -1)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
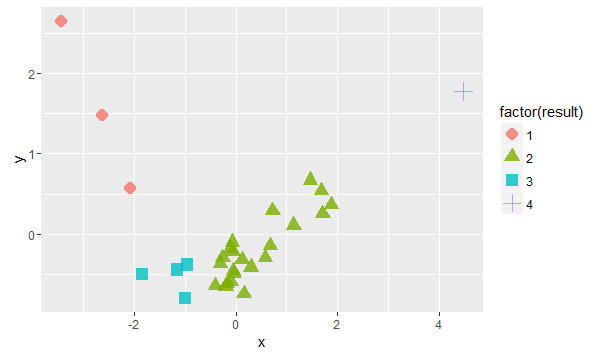
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result),shape = factor(result)))考虑将样本划分为3类,
接着,为了使得可视化效果更好,使用经典MDS对数据进行变换,画出散点图↓
所以,将1和14划为一组,13自成一组,其余的划为一组。
(2)K-means算法:依然把样本分为3类,编写如下R语言程序:
model <- kmeans(scale(X), centers = 3, nstart = 10)
model$cluster得到聚类分析结果:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 1 |
所以,将1、2、6、14划为一组,13自成一组,其余的划为一组。
(3)系统聚类:(↓R)
library(fpc)
model <- dbscan(X, eps = 2.5, MinPts = 5, scale = T, showplot = 1, method = "hybrid")
model$cluster得到分析结果:
0 1 0 1 1 1 1 0 1 1 1 1 0 0 0
这里结果表明将其划分为2类。
7.
【问题描述】:
下表是某年我国16个地区农民支出情况的抽样调查数据,每个地区调查了反映每人平均生活消费支出情况的六个经济指标。是通过统计分析软件用不同的方法进行聚类分析,并比较何种方法与人们观察到的实际情况较接近。
| 地区 | 食品 | 衣着 | 燃料 | 住房 | 交通和通讯 | 娱乐教育文化 |
|---|---|---|---|---|---|---|
| 北京 | 190.33 | 43.77 | 9.73 | 60.54 | 49.01 | 9.04 |
| 天津 | 135.2 | 36.4 | 10.47 | 44.16 | 36.49 | 3.94 |
| 河北 | 95.21 | 22.83 | 9.3 | 22.44 | 22.81 | 2.8 |
| 山西 | 104.78 | 25.11 | 6.4 | 9.89 | 18.17 | 3.25 |
| 内蒙 | 128.41 | 27.63 | 8.94 | 12.58 | 23.99 | 2.27 |
| 辽宁 | 145.68 | 32.83 | 17.79 | 27.29 | 39.09 | 3.47 |
| 吉林 | 159.37 | 33.38 | 19.27 | 11.81 | 25.29 | 5.22 |
| 黑龙江 | 116.22 | 29.57 | 13.24 | 11.81 | 25.29 | 5.22 |
| 上海 | 221.11 | 38.64 | 12.53 | 115.65 | 50.82 | 5.89 |
| 江苏 | 144.98 | 29.12 | 11.67 | 42.6 | 27.3 | 5.74 |
| 浙江 | 169.92 | 32.75 | 12.72 | 47.12 | 34.35 | 5 |
| 安徽 | 135.11 | 23.09 | 15.62 | 23.54 | 18.18 | 6.39 |
| 福建 | 144.92 | 21.26 | 16.96 | 19.52 | 21.75 | 6.73 |
| 山西 | 140.54 | 21.5 | 17.64 | 19.19 | 15.97 | 4.94 |
| 山东 | 115.84 | 30.26 | 12.2 | 33.6 | 33.77 | 3.85 |
| 河南 | 101.18 | 23.26 | 8.46 | 20.2 | 20.5 | 4.3 |
【解析】:
(1)层次聚类法:编写如下的R语言程序,数据从csv文件中读取。
consumptionData <- read.csv("*C:\\Users\\lenovo\\Desktop\\Book1.csv*", header = TRUE, sep = ",")
X <- consumptionData[,-1]
d <- dist(scale(X), method = 'euclidean')
heatmap(as.matrix(d),labRow = consumptionData$city, labCol = consumptionData$city)
kinds <- 5
model1 <- hclust(d, method = 'average')
result <- cutree(model1, k = kinds)
plclust(model1, -1, labels = consumptionData$city)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result), shape = factor(result)))考虑将样本划分为5类,
接着,为了使得可视化效果更好,使用经典MDS对数据进行变换,画出散点图↓
可见,北京、上海为一线城市,自成一类;江苏、浙江等为第二线省份;内蒙古等为一类省份;安徽等为一类省份。
(2)K-means算法:编写如下的R语言程序
model <- kmeans(scale(X), centers = 5, nstart = 10)
table(consumptionData$city, model$cluster)得到如下的类别划分结果:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| Anhui | 1 | 0 | 0 | 0 | 0 |
| Beijing | 0 | 0 | 0 | 0 | 1 |
| Fujian | 1 | 0 | 0 | 0 | 0 |
| Hebei | 0 | 0 | 1 | 0 | 0 |
| Heilongjiang | 1 | 0 | 0 | 0 | 0 |
| Henan | 0 | 0 | 1 | 0 | 0 |
| InnerMongolia | 0 | 0 | 1 | 0 | 0 |
| Jiangsu | 0 | 0 | 0 | 1 | 0 |
| Jiangxi | 1 | 0 | 0 | 0 | 0 |
| Jilin | 1 | 0 | 0 | 0 | 0 |
| Liaoning | 0 | 0 | 0 | 1 | 0 |
| Shandong | 0 | 0 | 0 | 1 | 0 |
| Shanghai | 0 | 1 | 0 | 0 | 0 |
| Shanxi | 0 | 0 | 1 | 0 | 0 |
| Tianjin | 0 | 0 | 0 | 1 | 0 |
| Zhejiang | 0 | 0 | 0 | 1 | 0 |
这个结果与层次聚类法的结果十分相似。
8.
【问题描述】:
某公司为掌握其新产品的动向,向12个代理商做调查,要他们对产品基于评估(对产品式样、包装及耐久性,用10分制打分,高分表示性能良好,低分制则较差)并说明是否购买,调查结果如下,是做fisher判别
| 式样 | 包装 | 耐久性 | ||
|---|---|---|---|---|
| 购买组样品 | 1 | 9 | 8 | 7 |
| 2 | 7 | 6 | 6 | |
| 3 | 10 | 7 | 8 | |
| 4 | 8 | 4 | 5 | |
| 5 | 9 | 9 | 7 | |
| 6 | 8 | 6 | 7 | |
| 7 | 7 | 5 | 6 | |
| 非购买组样品 | 1 | 4 | 4 | 4 |
| 2 | 3 | 6 | 6 | |
| 3 | 6 | 3 | 3 | |
| 4 | 2 | 4 | 5 | |
| 5 | 1 | 2 | 2 | |
【解析】:
利用Matlab实现Fisher线性分类器,程序如下:
function [w, y1, y2, Jw] = FisherLinearDiscriminate(data, label)
% FLD Fisher Linear Discriminant.
% data: D*N data
% label: {+1,-1}
% Reference: M.Bishop Pattern Recognition and Machine Learning p186-p189
% Copyright: LiFeitengup@CSDN
% compute means and scatter matrix
%-------------------------------
inx1 = find(label == 1);
inx2 = find(label == -1);
n1 = length(inx1);
n2 = length(inx2);
m1 = mean(data(:,inx1),2);
m2 = mean(data(:,inx2),2);
S1 = (data(:,inx1)-m1*ones(1,n1))*(data(:,inx1)-m1*ones(1,n1))';
S2 = (data(:,inx2)-m2*ones(1,n2))*(data(:,inx2)-m2*ones(1,n2))';
Sw = S1 + S2;
% compute FLD
%-------------------------------
W = inv(Sw)*(m1-m2);
y1 = W'*m1; %label=+1
y2 = W'*m2; %label=-1
w = W;
Jw = (y1-y2)^2/(W'*Sw*W);
end
data = [9 7 10 8 9 8 7 4 3 6 2 1;
8 6 7 4 9 6 5 4 6 3 4 2;
7 6 8 5 7 7 6 4 6 3 5 2];
label = [1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1];
[w, y1, y2, Jw] = FisherLinearDiscriminate(data, label);
w0 = (y1 + y2) / 2;
figure(1);
scatter3(data(1,1:7), data(2,1:7), data(3,1:7));
hold on;
scatter3(data(1,8:12), data(2,8:12), data(3,8:12));
hold on;
[x, y] = meshgrid(0:0.01:10);
z = (w0 - w(1) * x - w(2) * y) / w(3);
mesh(x, y, z);于是可以设计出Fisher分类器:
其中, w=(0.2197,−0.0792,0.1778)T , w0=1.7964 。
将样本点绘制在三维空间中,可以得到
↑可见,Fisher判别平面将两类训练集一分为二,没有出现误划。
9.
【问题描述】:
人文发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的,该报告建议,目前对人文发展的衡量应当以人生的三大要素为重点,衡量人生三大要素的指示指标分别要用出生时的预期寿命、成人识字率和实际人均GDP,将以上三个指示指标的数值合成为一个复合指数,即为人文发展指数,资料来源:UNDP《人类发展报告》1995年,今从1995年世界各国人文发展指数的排序中,选取高发展水平、中等发展水平的国家各五个作为两组样品,另选四个国家作为待判样品作距离判别分析。
| 类别 | 序号 | 国家名称 | 出生时预期寿命 | 成人识字率 | 人均GDP |
|---|---|---|---|---|---|
| 第一类(高发展水平国家) | 1 | 美国 | 76 | 90 | 5374 |
| 2 | 日本 | 79.5 | 99 | 5359 | |
| 3 | 瑞士 | 78 | 99 | 5372 | |
| 4 | 阿根廷 | 72.1 | 95.9 | 5242 | |
| 5 | 阿联酋 | 73.8 | 77.7 | 5370 | |
| 第二类(中等发展水平国家) | 6 | 保加利亚 | 71.2 | 93 | 4250 |
| 7 | 古巴 | 75.3 | 94.9 | 3412 | |
| 8 | 巴拉圭 | 70 | 91.2 | 3390 | |
| 9 | 格鲁尼亚 | 72.8 | 99 | 2300 | |
| 10 | 南非 | 62.9 | 80.6 | 3799 | |
| 待判样品 | 11 | 保加利亚 | 71.2 | 93 | 4250 |
| 12 | 罗马尼亚 | 69.9 | 96.9 | 2840 | |
| 13 | 希腊 | 77.6 | 93.8 | 5233 | |
| 14 | 哥伦比亚 | 69.3 | 90.3 | 5158 |
【解析】:
编写如下的Matlab程序:
training = [76 99 5374;
79.5 99 5359;
78 99 5372;
72.1 95.9 5242;
73.8 77.7 5370;
71.2 93 4250;
75.3 94.9 3412;
70 91.2 3390;
72.8 99 2300;
62.9 80.6 3799];
group = ['level1'; 'level1'; 'level1'; 'level1'; 'level1'; 'level2'; 'level2'; 'level2'; 'level2'; 'level2'];
sample = [68.5 79.3 1950;
69.9 96.9 2840;
77.6 93.8 5233;
69.3 90.3 5158];
[class, err] = classify(sample, training, group, 'linear');
class
err
figure(1);
scatter3(training(1:5, 1), training(1:5, 2), training(1:5, 3), 'bl');
hold on;
scatter3(training(6:10, 1), training(6:10, 2), training(6:10, 3), 'r');
hold on;
scatter3(sample(1:2, 1), sample(1:2, 2), sample(1:2, 3), 'g');
hold on;
scatter3(sample(3:4, 1), sample(3:4, 2), sample(3:4, 3), 'y');
hold on;↓判别的结果为中国和罗马尼亚属于第二类(中等发展水平国家),希腊和哥伦比亚属于第一类(高发展水平国家)。绘制出的散点图如下所示,其中绿色为中国和罗马尼亚,黄色为希腊和哥伦比亚。

10.
【问题描述】:
为了更深入地了解我国人口的文化程度状况,现利用1990年全国人口普查数据对全国30个省、直辖市、自治区进行聚类分析,原始数据如下表。分析选用了三个指标:大学以上文化程度的人口比例(DXBZ)、初中文化程度的人口比例(CZBZ)、文盲半文盲人口比例(WMBZ)来反映较高、中等、较低的文化程度人口的状况。
(1)计算样本的Euclid距离,分别用最长距离法、均值法、重心法和Ward法作聚类分析,并画出相应的谱系图。如果将所有样本分为四类,试写出各种方法的分类结果。
(2)用动态规划方法分四类,写出相应的分类结果。
| 地区 | DXBZ | CZBZ | WMBZ | 地区 | DXBZ | CZBZ | WMBZ |
|---|---|---|---|---|---|---|---|
| 北京 | 9.30 | 30.55 | 8.70 | 河南 | 0.85 | 26.55 | 16.15 |
| 天津 | 4.67 | 29.38 | 8.92 | 湖北 | 1.57 | 23.16 | 15.79 |
| 河北 | 0.96 | 24.69 | 15.21 | 湖南 | 1.14 | 22.57 | 12.10 |
| 山西 | 1.38 | 29.24 | 11.30 | 广东 | 1.34 | 23.04 | 10.45 |
| 内蒙古 | 1.48 | 25.47 | 15.39 | 广西 | 0.79 | 19.14 | 10.61 |
| 辽宁 | 2.60 | 32.32 | 8.81 | 海南 | 1.24 | 22.53 | 13.97 |
| 吉林 | 2.15 | 26.31 | 10.49 | 四川 | 0.96 | 21.65 | 16.24 |
| 黑龙江 | 2.14 | 28.46 | 10.87 | 四川 | 0.96 | 21.65 | 16.24 |
| 上海 | 6.53 | 31.59 | 11.04 | 云南 | 0.81 | 13.85 | 25.44 |
| 江苏 | 1.47 | 26.43 | 17.23 | 西藏 | 0.57 | 3.85 | 44.43 |
| 浙江 | 1.17 | 23.74 | 17.46 | 陕西 | 1.67 | 24.36 | 17.62 |
| 安徽 | 0.88 | 19.97 | 24.43 | 甘肃 | 1.10 | 16.85 | 27.93 |
| 福建 | 1.23 | 16.87 | 15.63 | 青海 | 1.49 | 17.76 | 27.70 |
| 江西 | 0.99 | 18.84 | 16.22 | 宁夏 | 1.61 | 20.27 | 22.06 |
| 山东 | 0.98 | 25.18 | 16.87 | 新疆 | 1.85 | 20.66 | 12.75 |
【解析】:
(1)编写如下的R语言程序,计算样本的Euclidean距离。
eduLevel <- read.csv("C:\\Users\\lenovo\\Desktop\\Book1.csv",header = TRUE, sep = ",")
X <- eduLevel[,-1]
d <- dist(scale(X), method = 'euclidean')计算得到的结果如下所示:
1 2 3 4 5 6
2 2.5079170
3 4.6857035 2.3019024
4 4.2959228 1.8039758 0.9399503
5 4.3944976 2.0267019 0.3100576 0.8254167
6 3.6299646 1.2195791 1.7576168 0.8952417 1.5493019
7 3.9315549 1.4674278 0.9317467 0.6482392 0.7504160 1.0491364
8 3.8923692 1.3982869 1.0586160 0.4339814 0.8509429 0.7377850
9 1.5366735 1.1047217 3.2642179 2.8084129 2.9651112 2.1456970
10 4.4267279 2.1006361 0.4787978 0.9077872 0.2891008 1.5953600
11 4.6764200 2.3876265 0.3531529 1.2235189 0.4289354 1.9765734
12 5.2920620 3.2801539 1.4408375 2.3237337 1.5302906 3.0415855
13 4.9962087 2.9202433 1.3060070 2.1298048 1.4327314 2.8124863
14 4.9879677 2.8142055 0.9791512 1.8532057 1.1359749 2.5876656
15 4.7038653 2.3542003 0.2325878 1.0165142 0.3359695 1.8121611
16 4.7133609 2.3182390 0.3374037 0.8278320 0.3971652 1.6537074
17 4.4486265 2.1627689 0.4226744 1.1719777 0.3896500 1.8584956
18 4.6223959 2.2544768 0.5471008 1.1184841 0.6715998 1.8497048
19 4.4810853 2.0926126 0.7117096 1.0343031 0.7665879 1.6961709
20 4.9759926 2.7059410 1.1041512 1.7071680 1.2780311 2.4056610
21 4.6032501 2.2714186 0.4214002 1.1688495 0.5376976 1.9058726
22 4.8413151 2.5647399 0.5218575 1.4335069 0.7017735 2.2053846
23 5.6821710 3.7986133 2.0475042 2.9749037 2.1719924 3.6959492
24 5.7883753 3.9583294 2.2442609 3.1693233 2.3621934 3.8818716
25 7.9859267 6.6710568 5.1638710 6.0652753 5.2529014 6.7307005
26 4.4043230 2.1491260 0.4998567 1.1687817 0.3604245 1.8245068
27 5.5790971 3.7744757 2.1160352 2.9997768 2.1883371 3.6771920
28 5.3377510 3.5672580 2.0210296 2.8725387 2.0590996 3.5104481
29 4.8186167 2.8250665 1.2112484 2.0538539 1.2301677 2.7012342
30 4.3767932 2.1591311 0.8840645 1.4576084 0.8921172 2.0418100
7 8 9 10 11 12
2
3
4
5
6
7
8 0.3600082
9 2.5231009 2.4268835
10 0.9572380 0.9693732 2.9760847
11 1.1388353 1.2781240 3.2834039 0.4755084
12 2.2173503 2.3677507 4.0129802 1.4629511 1.1182973
13 1.7751660 2.0795075 3.8093320 1.6042588 1.1645993 1.2772731
14 1.5783324 1.8499334 3.7257041 1.2917584 0.8342850 1.0943322
15 1.0649649 1.1433110 3.2705295 0.3394169 0.2711551 1.3160227
16 1.0223564 1.0319408 3.2489007 0.3640672 0.5258015 1.5393033
17 0.9240584 1.1328132 3.0847800 0.5766857 0.3222702 1.3046557
18 0.8524209 1.1275936 3.2753820 0.9454631 0.7292930 1.6791419
19 0.6966700 0.9986770 3.1417674 1.0541664 0.9310212 1.9186413
20 1.3975247 1.7090549 3.7246088 1.5328149 1.1961048 1.8180130
21 0.9179096 1.1697352 3.2503633 0.7850780 0.5011037 1.4488522
22 1.2563742 1.4754466 3.4969424 0.8490626 0.3981838 1.1102947
23 2.7477729 2.9783102 4.5321877 2.1923434 1.7645284 0.8840365
24 2.9385431 3.1677404 4.6646561 2.3742691 1.9549944 1.0240915
25 5.8654520 6.0610060 7.1193300 5.1937573 4.8465005 3.7483477
26 1.0226485 1.1445478 3.0115315 0.3634436 0.2896743 1.2285151
27 2.8304711 3.0042608 4.4132326 2.1287997 1.7864622 0.7016984
28 2.6887646 2.8532727 4.1759308 1.9878753 1.6780856 0.6531804
29 1.8411181 2.0196721 3.5594982 1.2042119 0.8667955 0.5044283
30 0.9958719 1.3259214 3.1179869 1.1413015 0.8815281 1.6226743
13 14 15 16 17 18
2
3
4
5
6
7
8
9
10
11
12
13
14 0.3598412
15 1.3940355 1.0547307
16 1.6195897 1.2807005 0.2558243
17 1.0592217 0.7838317 0.4834798 0.6851052
18 1.0535236 0.8251935 0.7654856 0.8614349 0.5455278
19 1.2294583 1.0455410 0.9340074 0.9835525 0.7114148 0.2540625
20 0.7946200 0.7451584 1.2989826 1.4277362 1.0407148 0.6303693
21 0.9634393 0.6925593 0.5978235 0.7552413 0.3156283 0.2511668
22 0.8098546 0.4662293 0.5912265 0.8147478 0.4179470 0.5722001
23 1.2157545 1.2687608 2.0004555 2.2424544 1.8465004 2.0758068
24 1.3988772 1.4682225 2.1910441 2.4328922 2.0378131 2.2764274
25 4.3645250 4.4623215 5.0614000 5.2859615 4.9645580 5.2632010
26 1.2911220 1.0031510 0.4086485 0.6042337 0.3163675 0.8330112
27 1.6143654 1.5716495 2.0038010 2.2340859 1.9217564 2.2822358
28 1.5957303 1.5397850 1.8990088 2.1301350 1.8006958 2.2036566
29 1.0348036 0.8687461 1.1143224 1.3613674 0.9518609 1.3840183
30 0.8060034 0.7167807 1.0364833 1.2017547 0.5946436 0.5045466
19 20 21 22 23 24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 0.7119306
21 0.4723393 0.7544083
22 0.8195330 0.8524282 0.3643507
23 2.3045003 1.9397409 1.8955337 1.5701437
24 2.5034838 2.1332893 2.0946242 1.7704832 0.2034588
25 5.4909486 5.1095948 5.0672944 4.7348903 3.1949646 2.9944379
26 0.9816173 1.3490393 0.6124201 0.6177919 1.8930502 2.0746495
27 2.5147225 2.3086834 2.0599749 1.7288197 0.6271003 0.6152875
28 2.4267821 2.2840717 1.9710517 1.6601331 0.7843551 0.8018722
29 1.5968088 1.5764910 1.1426498 0.8706076 1.0739024 1.2313761
30 0.5679284 0.6855035 0.4798381 0.6836312 1.8996725 2.0878951
25 26 27 28 29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 4.9271870
27 3.0674899 1.8636170
28 3.2216611 1.7187512 0.2608285
29 4.0413404 0.8943896 0.9949259 0.8510835
30 5.0500586 0.8908598 2.1272359 2.0277721 1.2293341利用如下语句绘制热力图:(↓R)
heatmap(as.matrix(d),labRow = eduLevel$region, labCol = eduLevel$region)下面进行各种方法的聚类分析:
①最长距离法:
kinds <- 4
model1 <- hclust(d, method = 'complete')
result <- cutree(model1, k = kinds)
plot(model1, -1, labels = eduLevel$region)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result), shape = factor(result)))↓得到谱系图
利用经典MDS变换,↓散点图
②均值法:
kinds <- 4
model1 <- hclust(d, method = 'average')
result <- cutree(model1, k = kinds)
plot(model1, -1, labels = eduLevel$region)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result), shape = factor(result)))③重心法:
kinds <- 4
model1 <- hclust(d, method = 'centroid')
result <- cutree(model1, k = kinds)
plot(model1, -1, labels = eduLevel$region)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result), shape = factor(result)))④离差平方和法:
kinds <- 4
model1 <- hclust(d, method = 'ward')
result <- cutree(model1, k = kinds)
plclust(model1, -1, labels = eduLevel$region)
rect.hclust(model1, k = kinds, border = "red")
mds <- cmdscale(d, k = 2, eig = T)
x <- mds$points[,1]
y <- mds$points[,2]
library(ggplot2)
p <- ggplot(data.frame(x,y),aes(x,y))
p + geom_point(size = kinds, alpha = 0.8, aes(colour = factor(result), shape = factor(result)))(2)利用K-means算法,编写如下R语言程序:
model <- kmeans(scale(X), centers = 4, nstart = 10)
table(eduLevel$region, model$cluster)得到如下的分类结果:
1 2 3 4
Anhui 0 1 0 0
Beijing 0 0 0 1
Fujian 0 1 0 0
Gansu 0 1 0 0
Guangdong 1 0 0 0
Guangxi 1 0 0 0
Guizhou 0 1 0 0
Hainan 1 0 0 0
Hebei 1 0 0 0
Heilongjiang 1 0 0 0
Henan 1 0 0 0
Hubei 1 0 0 0
Hunan 1 0 0 0
InnerMongolia 1 0 0 0
Jiangsu 1 0 0 0
Jiangxi 0 1 0 0
Jilin 1 0 0 0
Liaoning 1 0 0 0
Ningxia 0 1 0 0
Qinghai 0 1 0 0
Shandong 1 0 0 0
Shanghai 0 0 0 1
Shanxi(Taiyuan) 1 0 0 0
Shanxi(Xi'an) 1 0 0 0
Sichuan 1 0 0 0
Tianjin 0 0 0 1
Tibet 0 0 1 0
Xinjiang 1 0 0 0
Yunnan 0 1 0 0
Zhejiang 1 0 0 0附:
用ggfortify软件包做更好看的二维可视化