JAVA算法：最长公共子序列—动态规划算法

最长公共子序列—动态规划算法（Longest Common Subsequence）

让我们来讨论如何使用动态规划算法来解决LCS问题。

LCS问题陈述：给定两个序列，找出两个序列中存在的最长子序列的长度。

子序列是以相同的相对顺序出现的序列，但不一定是连续的。例如，“abc”、“abg”、“bdf”、“aeg”、“'”acefg“等等都是“abcdefg”的子序列。所以一个长度为n的字符串有2^n个不同的可能子序列。

它是一个经典的计算机科学问题，是diff（一个输出两个文件之间差异的文件比较程序）的基础，在生物信息学中有着广泛的应用。

举例：

对于给定的字符串 “ABCDGH” 和 “AEDFHR”，其最长公共子序列为： “ADH”，最长公共子序列的长度为：3。
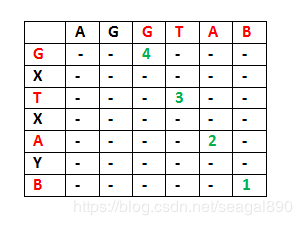
对于给定的字符串 “AGGTAB” 和 “GXTXAYB”，其最长公共子序列为：“GTAB”，最长公共子序列的长度为：4。

算法分析

这个问题的简单解决方案是生成两个给定序列的所有子序列，并找到最长的匹配子序列。根据时间复杂性，这个解是指数的。让我们看看这个问题如何具有动态规划（DP）问题的两个重要特性。

最优子结构

输入序列分别为长度m和n的X[0..m-1]和Y[0..n-1]。

设L（x[0..m-1]，y[0..n-1]）为两个序列X和Y的LCS的长度，下面是L（X[0..m-1]，Y[0..n-1]）的递归定义。

如果两个序列的最后一个字符匹配（或X[m-1]==Y[n-1]），则

L（X[0..m-1]，Y[0..n-1]）= 1+L（X[0..m-2]，Y[0..n-2]）

如果两个序列的最后一个字符不匹配（或X[m-1]！= Y[n-1）]

L（X[0..m-1]，Y[0..n-1]）=最大值（L（X[0..m-2]，Y[0..n-1]），L（X[0..m-1]，Y[0..n-2]））

例如：

1）考虑输入字符串“aggtab”和“gxtxayb”。最后一个字符与字符串匹配。因此，LCS的长度可以写为：

L（“aggtab”，“gxtxayb”）=1+L（“aggta”，“gxtxay”）。

 

2）考虑输入字符串“abcdgh”和“aedfhr”。最后一个字符与字符串不匹配。因此，LCS的长度可以写为：

L（“abcdgh”，“aedfhr”）=max（L（“abcdg”，“aedfhr”），L（“abcdgh”，“aedfh”））

因此，LCS问题具有最优的子结构性质，利用子问题的解可以解决主要问题。

重叠子问题

下面是LCS问题的简单递归实现。实现只遵循上面提到的递归结构。

package com.bean.algorithm.basic;

public class LongestCommonSubsequence {
	/* A Naive recursive implementation of LCS problem in java */

	/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
	int lcs(char[] X, char[] Y, int m, int n) {
		if (m == 0 || n == 0)
			return 0;
		if (X[m - 1] == Y[n - 1])
			return 1 + lcs(X, Y, m - 1, n - 1);
		else
			return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n));
	}

	/* Utility function to get max of 2 integers */
	int max(int a, int b) {
		return (a > b) ? a : b;
	}

	public static void main(String[] args) {
		LongestCommonSubsequence lcs = new LongestCommonSubsequence();
		String s1 = "AGGTAB";
		String s2 = "GXTXAYB";

		char[] X = s1.toCharArray();
		char[] Y = s2.toCharArray();
		int m = X.length;
		int n = Y.length;

		System.out.println("Length of LCS is" + " " + lcs.lcs(X, Y, m, n));
	}

}

输出结果：

Length of LCS is 4

上述幼稚的递归方法在最坏情况下的时间复杂度为O（2^n），当x和y的所有字符都不匹配（即lcs的长度为0）时，最坏情况发生。考虑到上述实现，下面是输入字符串“axyt”和“ayzx”的部分递归树。

 在上面的部分递归树中，LCS（“axy”，“ayz”）被求解两次。如果我们画出一个完整的递归树，那么我们可以看到有许多子问题被一次又一次地解决。因此，该问题具有重叠的子结构性质，可以通过动态规划算法来避免同一子问题的重新计算。下面是LCS问题的动态规划算法实现。

package com.bean.algorithm.basic;

public class LongestCommonSubsequence2 {
	/* Dynamic Programming Java implementation of LCS problem */
	/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
	int lcs(char[] X, char[] Y, int m, int n) {
		int L[][] = new int[m + 1][n + 1];

		/*
		 * Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j]
		 * contains length of LCS of X[0..i-1] and Y[0..j-1]
		 */
		for (int i = 0; i <= m; i++) {
			for (int j = 0; j <= n; j++) {
				if (i == 0 || j == 0)
					L[i][j] = 0;
				else if (X[i - 1] == Y[j - 1])
					L[i][j] = L[i - 1][j - 1] + 1;
				else
					L[i][j] = max(L[i - 1][j], L[i][j - 1]);
			}
		}
		return L[m][n];
	}

	/* Utility function to get max of 2 integers */
	int max(int a, int b) {
		return (a > b) ? a : b;
	}

	public static void main(String[] args) {
		LongestCommonSubsequence2 lcs = new LongestCommonSubsequence2();
		String s1 = "AGGTAB";
		String s2 = "GXTXAYB";

		char[] X = s1.toCharArray();
		char[] Y = s2.toCharArray();
		int m = X.length;
		int n = Y.length;

		System.out.println("Length of LCS is" + " " + lcs.lcs(X, Y, m, n));
	}

}

程序运行结果：

Length of LCS is 4

上述实现的时间复杂度为O（mn），比简单递归实现的最坏情况下的时间复杂度要好得多。