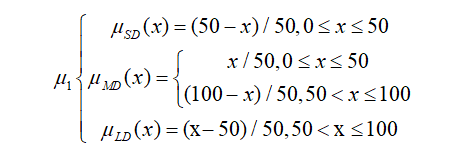Matlab语言实现模糊洗衣机控制器的设计
目录
1 引入
2 模糊洗衣机内部结构
3 模糊控制洗衣机的实现方法
4 实验过程
4.1 定义模糊控制器结构
4.2 定义输入、输出模糊集
4.3 定义隶属函数
4.4 建立模糊控制规则
4.5 模糊推理
4.5.1 规则匹配
4.5.2 规则触发
4.5.3 规则前提推理
4.5.4 每条规则的推理
4.5.5 模糊系统总的输出(聚合)
4.5.6 去模糊化
1 引入
模糊控制洗衣机题应用模糊逻辑利模糊推理方法、模仿人的思维进行判断操作的一种新型全自动洗衣机。普通微电脑洗衣机采用的是量化的固定程序,一经设定,便不能更改;而模糊控制洗衣机则是应用模糊控制器代替人脑来分析、判断,比普通微电脑洗衣机更灵活更方便适用。日本的松下、三洋和日立公司等先后推出了一个按钮的模糊控制洗衣机,我国许多家电企业也推出了各种类型的智能控制洗衣机。
海尔(Haier)XQB60-M981全自动洗衣机,其产品介绍中说:该款型全自动洗衣机的一大特点是“智能模糊”,可满足各种衣物洗涤要求,根据衣物重量与材质对洗衣机程序进行模糊控制,以确定水位的高低、时间的长短,选择最佳洗衣程序,精确洗衣,节水节电。
三洋(SANYO)XQG60-F1029全自动洗衣机,其产品介绍中说:这款洗衣机采用三洋最先开发的人工智能技术—模糊控制洗衣技术,能模仿人的感觉、思维、判断能力,通过多种传感器判断衣物重量、布质和衣物的洗涤状态,由智能电脑不断采集处理信息,决定水位的高低、洗衣粉的用量、洗涤时间和方式等,并自动完成整个洗衣过程。
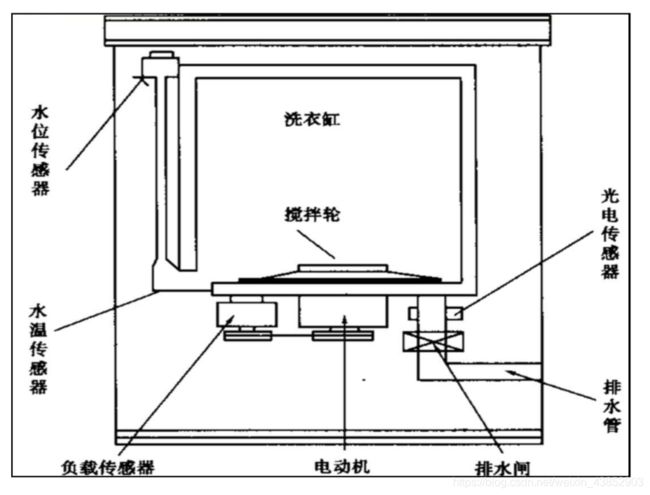
2 模糊洗衣机内部结构
模糊洗衣机结构剖面图
模糊洗衣机电路结构图
3 模糊控制洗衣机的实现方法
利用负载、质料、水位、水温以及洗涤剂等检测所得到的信息,进行分段评估计算,使其模糊化,再根据模糊规则进行推理,以决定最适当的和明确的水流/水位/洗涤时间/清洗方法以及脱水时间。
4 实验过程
4.1 定义模糊控制器结构
选用单变量二维模糊控制器。控制器的输入为衣物的污泥和油脂,输出为洗涤时间。
4.2 定义输入、输出模糊集
- 将污泥分为三个模糊集:SD(污泥少),MD(污泥中),LD(污泥多),取值范围为[0,100].
- 将油脂分为三个模糊集:NG(油脂少),MG(油脂中),LG(油脂多),取值范围为[0,100].
- 将洗涤时间分为5个模糊集:VS(很短),S(短),M(中等),L(长),VL(很长),取值范围为[0,60].
4.3 定义隶属函数
采用三角隶属函数实现污泥、油脂的模糊化。
对于污泥模糊化选用如下隶属函数:
对于油脂模糊化选用如下隶属函数:
Matlab实现污泥、油脂隶属度函数的设计,其仿真代码为:
clear all;
close all;
N = 2;
x = 0:0.1:100;
for i = 1 : N+1
f(i) = 100/N*(i-1);
end
u = trimf(x, [f(1), f(1), f(2)]);
figure(1);
plot(x, u);
for j = 2 : N
u = trimf(x, [f(j-1), f(j), f(j+1)]);
hold on;
plot(x,u);
end
u = trimf(x, [f(N), f(N+1), f(N+1)]);
hold on;
plot(x,u);
xlable('x');
ylable('Degree of membership');
Matlab实现洗涤时间隶属度函数的设计,其仿真代码为:
clear all;
close all;
z = 0 : 0.1 : 60;
u = trimf(z, [0,0,10]);
figure(1);
plot(z,u);
u = trimf(z, [0,10,25]);
hold on;
plot(z,u);
u = trimf(z, [10,25,40]);
hold on;
plot(z,u);
u = trimf(z, [25,40,60]);
hold on;
plot(z,u);
u = trimf(z, [40,60,60]);
hold on;
plot(z,u);
xlable('z');
ylable('Degree of membership');
输出时间隶属度函数为:
洗涤机模糊控制系统仿真的Matlab程序:
clear all;
close all;
a = newfis('fuzz_wash');
a = addvar(a, 'input', 'x', [0,100]);
a = addmf(a, 'input', 1, 'SD', 'trimf', [0,0,50]);
a = addmf(a, 'input', 1, 'MD', 'trimf', [0,50,100]);
a = addmf(a, 'input', 1, 'LD', 'trimf', [50,100,100]);
a = addvar(a, 'input', 'y', [0,100]);
a = addmf(a, 'input', 2, 'NG', 'trimf', [0,0,50]);
a = addmf(a, 'input', 2, 'MG', 'trimf', [0,50,100]);
a = addmf(a, 'input', 2, 'LG', 'trimf', [50,100,100]);
a = addvar(a, 'output', 'z', [0,60]);
a = addmf(a, 'output', 1, 'VS', 'trimf', [0,0,10]);
a = addmf(a, 'output', 1, 'S', 'trimf', [0,10,25]);
a = addmf(a, 'output', 1, 'M', 'trimf', [10,25,40]);
a = addmf(a, 'output', 1, 'L', 'trimf', [25,40,60]);
a = addmf(a, 'output', 1, 'VL', 'trimf', [40,60,60]);
rulelist = [1 1 1 1 1;
1 2 3 1 1;
1 3 4 1 1;
2 1 2 1 1;
2 2 3 1 1;
2 3 4 1 1;
3 1 3 1 1;
3 2 4 1 1;
3 3 5 1 1];
a = addrule(a, rulelist);
showrule(a)
a1 = setfis(a, 'DefuzzMethod', 'mom');
writefis(a1, 'wash');
a2 = readfis('wash');
figure(1);
plotfis(a2);
figure(2);
plotmf(a, 'input', 1);
figure(3);
plotmf(a, 'input', 2);
figure(4);
plotmf(a, 'output', 1);
ruleview('wash');
x = 60;
y = 70;
z = evalfis([x,y], a2);
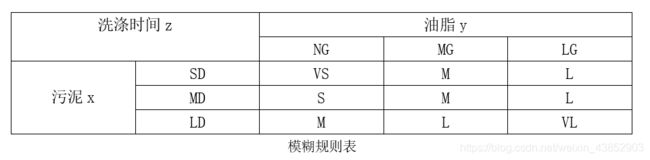
4.4 建立模糊控制规则
根据人的操作经验设计模糊规则,模糊规则设计标准为:“污泥越多,油脂越多,洗涤时间越长”;“污泥适中,油脂适中,洗涤时间适中”;“污泥越少,油脂越少,洗涤时间越短”。
4.5 模糊推理
简述推理过程:
4.5.1 规则匹配
当传感器测得污泥和油脂的信息之后,带入所属的隶属函数中求出隶属度,根据隶属度,得到相应的规则。
4.5.2 规则触发
从9条规则中触发相应的规则。
4.5.3 规则前提推理
在同一条规则中,通过取小运算表达式“与”,得到每一条规则总前提的可信度,由此得到洗衣机规则前提可信度。
4.5.4 每条规则的推理
进行“合成”运算,得到每条规则的输出(规则的可信度)。
4.5.5 模糊系统总的输出(聚合)
取各条推理结果的并。
4.5.6 去模糊化
模糊系统总的输出实际上是三个规则推理结果的并集,需要进行反模糊化,才能得到精确的推理结果。