标准DH建模与改进DH建模(四,完)——标准DH建模与改进DH建模实例对比
本文我们分别用SDH法和MDH来给同一个机器人模型建模,感受一下两种建模方法在串联机械臂里面的应用。
所用平台:Matlab
本文重点是建系以及提取DH参数表的过程
想要运行程序只需要把所有代码复制粘贴进matlab运行即可
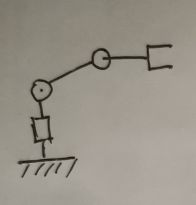
1. 机器人结构
我这边选的机器人模型有点特殊,需要自行增加坐标系。这是因为这里的Tool frame不能用DH法
2.尝试用标准DH建模
2.1 首先建系
我们按照标准DH建模规则建立如下坐标
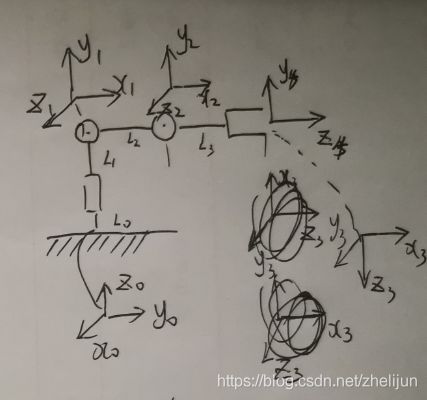
如果大家按照建系规则建系的话,不难得到坐标系1,2,4。但这里我们注意到中间加了个X3Y3Z3坐标系,原因是不加这个另外的坐标系的话,最后Tool frame不能运用DH法来写出它的四个参数,写出来也不对。原因是它不满足DH的两个条件:

加了3坐标系之后,以上两个条件又重新满足了,参数表只需要加一行即可。
2.2 写出参数表
接下来写出参数表:

2.3 写出转换方程
Matlab 代码:
syms q1 q2 q3;
l0 = 20;
l1 = 30;
l2 = 40;
l3 = 50;
DH = [0 pi/2 l0+l1 pi/2+q1;
l2 0 0 q2;
l3 pi/2 0 q3;
0 -pi/2 0 -pi/2];
transform matrix:
From frame 0 to frame 1:
SH0_1 = [cos(DH(1,4)) -sin(DH(1,4))*cos(DH(1,2)) sin(DH(1,4))*sin(DH(1,2)) DH(1,1)*cos(DH(1,4));
sin(DH(1,4)) cos(DH(1,4))*cos(DH(1,2)) -cos(DH(1,4))*sin(DH(1,2)) DH(1,1)*sin(DH(1,4));
0 sin(DH(1,2)) cos(DH(1,2)) DH(1,3) ;
0 0 0 1 ];
SH0_1 = simplify(SH0_1);
From frame 1 to frame 2:
SH1_2 = [cos(DH(2,4)) -sin(DH(2,4))*cos(DH(2,2)) sin(DH(2,4))*sin(DH(2,2)) DH(2,1)*cos(DH(2,4));
sin(DH(2,4)) cos(DH(2,4))*cos(DH(2,2)) -cos(DH(2,4))*sin(DH(2,2)) DH(2,1)*sin(DH(2,4));
0 sin(DH(2,2)) cos(DH(2,2)) DH(2,3) ;
0 0 0 1 ];
SH1_2 = simplify(SH1_2);
From frame 2 to frame 3:
SH2_3 = [cos(DH(3,4)) -sin(DH(3,4))*cos(DH(3,2)) sin(DH(3,4))*sin(DH(3,2)) DH(3,1)*cos(DH(3,4));
sin(DH(3,4)) cos(DH(3,4))*cos(DH(3,2)) -cos(DH(3,4))*sin(DH(3,2)) DH(3,1)*sin(DH(3,4));
0 sin(DH(3,2)) cos(DH(3,2)) DH(3,3) ;
0 0 0 1 ];
SH2_3 = simplify(SH2_3);
From frame 3 to frame 4:
SH3_4 = [cos(DH(4,4)) -sin(DH(4,4))*cos(DH(4,2)) sin(DH(4,4))*sin(DH(4,2)) DH(4,1)*cos(DH(4,4));
sin(DH(4,4)) cos(DH(4,4))*cos(DH(4,2)) -cos(DH(4,4))*sin(DH(4,2)) DH(4,1)*sin(DH(4,4));
0 sin(DH(4,2)) cos(DH(4,2)) DH(4,3) ;
0 0 0 1 ];
SH3_4 = simplify(SH3_4);
最后全部乘起来得到正运动学公式
SHbase_tool(q1,q2,q3)=simplify(SH0_1*SH1_2*SH2_3*SH3_4)
2.4 验证结果
我们随便带入三个关节角,比如(pi/2/,pi/6,-pi/7)
命令行输入
double(SHbase_tool(pi/2,pi/6,-pi/7))
得到结果:
>>double(SHbase_tool(pi/2,pi/6,-pi/7))
ans =
0 0.0747 -0.9972 -84.5012
-1.0000 0 0 0
0 0.9972 0.0747 73.7365
0 0 0 1.0000
3.用MDH建模
3.1 建系
同样的模型,我们试着用MDH再建一次模型,参照MDH建模规则,得到如下坐标系。注意坐标系2和坐标系1原点重合。

3.2 写出参数表

3.3 写出转换方程
MDH = [0 0 l0+l1 pi/2+q1;
pi/2 0 0 q2;
0 l2 0 pi/2+q3;
pi/2 0 l3 -pi/2];
Transform matrix
From frame 0 to frame 1:
MH0_1 = [cos(MDH(1,4)) -sin(MDH(1,4)) 0 MDH(1,2);
cos(MDH(1,1))*sin(MDH(1,4)) cos(MDH(1,1))*cos(MDH(1,4)) -sin(MDH(1,1)) -MDH(1,3)*sin(MDH(1,1));
sin(MDH(1,1))*sin(MDH(1,4)) sin(MDH(1,1))*cos(MDH(1,4)) cos(MDH(1,1)) MDH(1,3)*cos(MDH(1,1));
0 0 0 1];
MH0_1 = simplify(MH0_1);
From frame 1 to frame 2:
MH1_2 = [cos(MDH(2,4)) -sin(MDH(2,4)) 0 MDH(2,2);
cos(MDH(2,1))*sin(MDH(2,4)) cos(MDH(2,1))*cos(MDH(2,4)) -sin(MDH(2,1)) -MDH(2,3)*sin(MDH(2,1));
sin(MDH(2,1))*sin(MDH(2,4)) sin(MDH(2,1))*cos(MDH(2,4)) cos(MDH(2,1)) MDH(2,3)*cos(MDH(2,1));
0 0 0 1];
MH1_2 = simplify(MH1_2);
From frame 2 to frame 3:
MH2_3 = [cos(MDH(3,4)) -sin(MDH(3,4)) 0 MDH(3,2);
cos(MDH(3,1))*sin(MDH(3,4)) cos(MDH(3,1))*cos(MDH(3,4)) -sin(MDH(3,1)) -MDH(3,3)*sin(MDH(3,1));
sin(MDH(3,1))*sin(MDH(3,4)) sin(MDH(3,1))*cos(MDH(3,4)) cos(MDH(3,1)) MDH(3,3)*cos(MDH(3,1));
0 0 0 1];
MH2_3 = simplify(MH2_3);
From frame 3 to frame 4:
MH3_4 = [cos(MDH(4,4)) -sin(MDH(4,4)) 0 MDH(4,2);
cos(MDH(4,1))*sin(MDH(4,4)) cos(MDH(4,1))*cos(MDH(4,4)) -sin(MDH(4,1)) -MDH(4,3)*sin(MDH(4,1));
sin(MDH(4,1))*sin(MDH(4,4)) sin(MDH(4,1))*cos(MDH(4,4)) cos(MDH(4,1)) MDH(4,3)*cos(MDH(4,1));
0 0 0 1];
MH3_4 = simplify(MH3_4);
最后得到正运动学方程
MHbase_tool(q1,q2,q3)=simplify(MH0_1*MH1_2*MH2_3*MH3_4)
3.4 验证
同样地,代入三个关节角(pi/2/,pi/6,-pi/7)
命令行输入
double(MHbase_tool(pi/2,pi/6,-pi/7))
得到结果:
>> double(MHbase_tool(pi/2,pi/6,-pi/7))
ans =
0 0.0747 -0.9972 -84.5012
-1.0000 0 0 0
0 0.9972 0.0747 73.7365
0 0 0 1.0000
果然,跟SDH建模得到的结果一样。以上